第352回 シーズン36 エピソード2

三角形と面積が等しい正方形を作る（後編）

僕の部屋

ユーリ「これ、三平方の定理になるじゃん！！！」

$$ \PS{\SQRT{ab}}^2 + \PS{\frac{a - b}{2}}^2 = \PS{\frac{a + b}{2}}^2 $$

僕「そうなんだよ！　こんなふうに名前を付けてみると、斜辺が $C$ の直角三角形が現れる」

$$ \begin{array}{ccccc} \PS{\SQRT{ab}}^2 &+& \PS{\frac{a - b}{2}}^2 &=& \PS{\frac{a + b}{2}}^2 \\ \vdots & & \vdots & & \vdots \\ A^2 &+& B^2 &=& C^2 \\ \end{array} $$

ユーリ「てことは、 $B,C$ を作ればいい？」

僕「そういうことになるね。 一辺の長さ $B$ が、 $$ B = \frac{a - b}{2} $$ となって、斜辺の長さ $C$ が、 $$ C = \frac{a + b}{2} $$ となるような直角三角形を作図できれば、 もう一辺の長さ $A$ が求める長さ、つまり、 $$ A = \SQRT{ab} $$ になる」

ユーリ「数式、すっごーい！　 $a,b$ から $B,C$ は……作れそう！」

僕「うん、作れる。コンパスと定規で作れるよ。作ってみよう！」

ユーリ「おー！」

$(a - b)/2$ を作る

僕「まずは、 $a,b$ が与えられているときに、 $(a - b)/2$ を定規とコンパスで作図したい。 そのために……」

ユーリ「お兄ちゃん、ちょっと待って」

僕「おっと」

ユーリ「いま長方形を横の方が長いとして考えてるよね？ だって、もしも横が短くて $a < b$ だったら、 $a - b < 0$ でマイナスの長さになっちゃう」

僕「ああ、そうだね。よく気がつくなあ、ユーリ！　 でも、もしも縦の方が長い長方形だったら、 縦と横を入れ換えればいい」

ユーリ「いや、それはわかるけどさ。いちおー言っといただけ」

僕「つまり、 $a < b$ のときには縦を横を入れ換えればいいから、 $a > b$ でも一般性を失わない」

ユーリ「いっぱんせー？　急に難しいこと言い出したね？」

僕「いや、何も難しいことはとないよ。 ここからは、 $a > b$ という仮定を置いた上で議論を進めても一般性を失わないって言っただけ。 いま僕たちは、与えられた長方形がどんなものであってもかまわないという作図を考えている。 縦がどれだけ長くても横がどれだけ長くてもかまわない。 $a,b$ は任意の正の数」

ユーリ「そだね」

僕「『$a > b$ と仮定する』のように条件を付けてしまうと、 まるで、そういう特殊な長方形のことしか考えていないような誤解を与えてしまうかもしれない」

ユーリ「誤解を与えるって、誰に？」

僕「数学の議論をしている相手に対して。もしくは証明を読む相手に対して。 勝手に条件を付け加えると、論理に漏れがあるような印象を与えてしまう。 実際、ユーリもそこが気になったわけだ」

ユーリ「ふむふむ。確かに！」

僕「でも、たとえ与えられた長方形が $a < b$ だとしても、 縦と横を入れ換えれば $a > b$ という条件を満たすようにできるわけだから、 『$a > b$ と仮定する』としても、特殊な長方形のことしか考えてないわけじゃない。 そういう状況を短く表現したのが『一般性を失わない』という言い方なんだ」

ユーリ「わかった。 $a < b$ だとしても $a > b$ にできるからね」

僕「そうだね」

ユーリ「あれ、でも $a = b$ の場合が抜けてるよ……あ、ちがう、大丈夫だ。 $a = b$ のときはもう正方形なんだもん」

僕「そういうこと。だから、 $a < b, a = b, a > b$ という三つの場合があるけれど、 $a > b$ で考えてかまわない」

ユーリ「$a > b$ で考えても一般性を失わない」

僕「そういうこと」

ユーリ「$a - b$ の長さを作るのはカンタンだね。 角からコンパスをくるっと回せば、ここが $a - b$ になるってことでしょ？」

僕「そうだね。コンパスを使って、縦の長さ $b$ を横に持ってきたわけだ。 すると残りの部分が $a - b$ になる。 つまり、 $a, b$ が与えられていれば、定規とコンパスで $a - b$ の作図はできる」

ユーリ「うん。説明くどいけど」

僕「だからコンパスは《円を描く》ためというよりも《等しい長さを別の場所に移す》ために使っていることになる」

ユーリ「そだね。説明くどいけど」

僕「でも話は逆かも。コンパスの基本的な役目は《等しい長さを別の場所に移す》なのであって、 一点に針を置いてぐるっと回すことで《ある一点から等距離にあるすべての点》を描くことができる。 そうやって描いた図形のことを《円》と呼んでいるんだ」

ユーリ「平面上で？」

僕「おっと、そうだね。 《一つの平面上で、ある一点から等距離にあるすべての点の集合》が《円》だ」

ユーリ「空間だと球になっちゃう」

僕「その通り、球面だね。さてこれで、 $a - b$ が手に入った。ここから $(a - b)/2$ を作るのは……」

ユーリ「できるできる。円を二つ描いて交点を結べばいい」

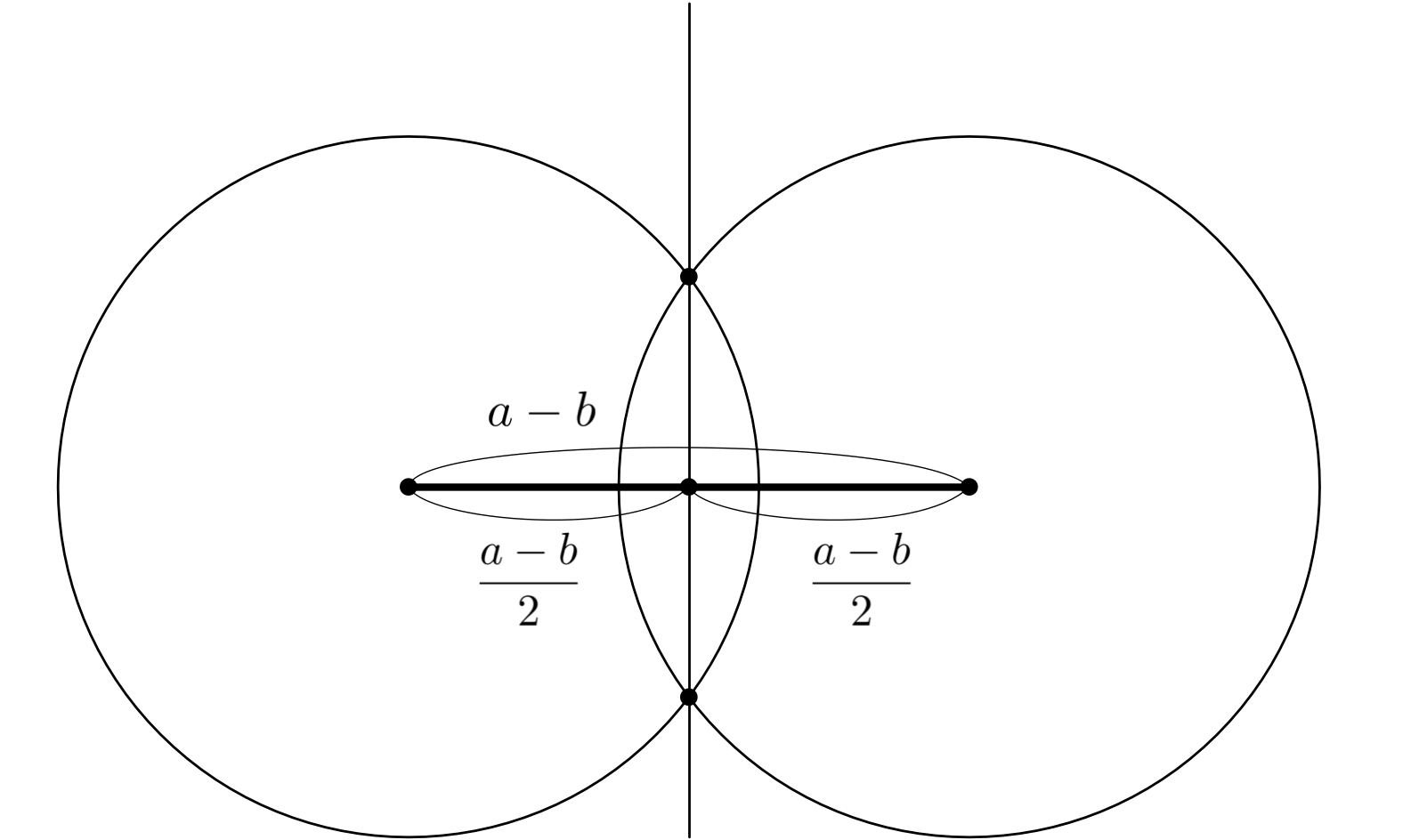
僕「うん。垂直二等分線を作図できるから、長さを半分にできるわけだ」

ユーリ「作図できる……あー、ちょっとまずいかも」

僕「何が？」

ユーリ「いま、適当な半径で描いちゃったけど、半径が短すぎたら交点ができない」

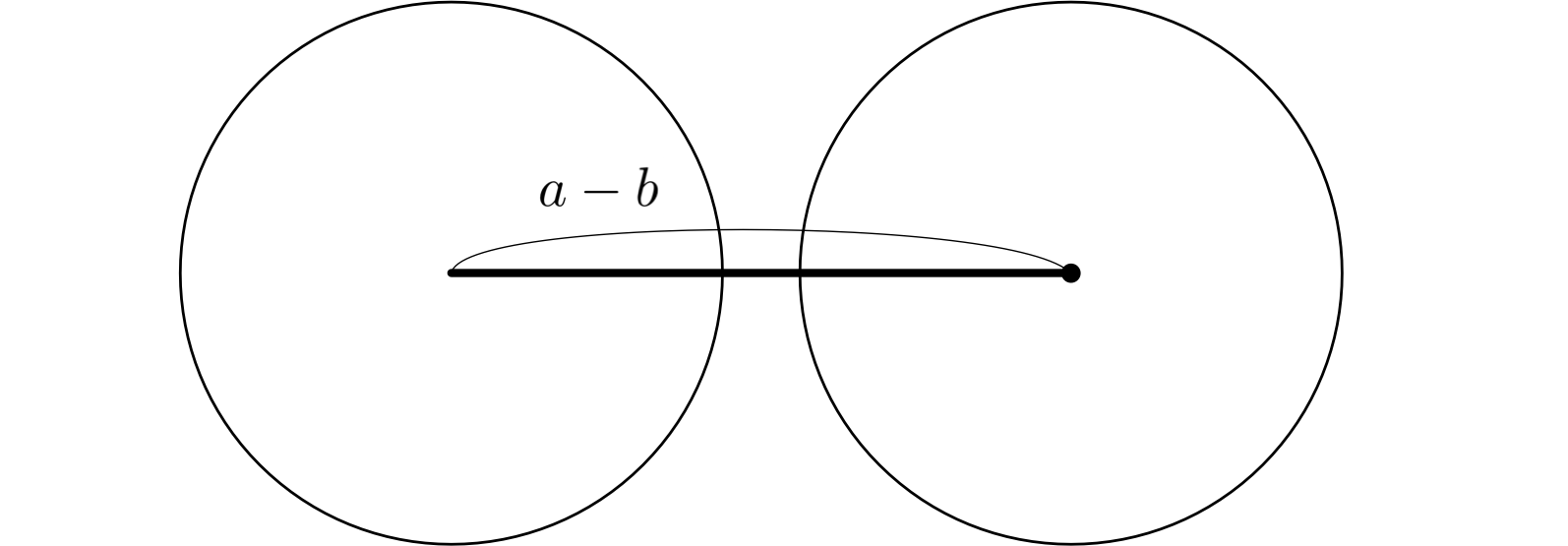
僕「おお、確かにね。だったら、二等分したい長さを使った二円を描けばいい。 いまの例だと、半径を $a - b$ にすれば確実に交点ができるよ」

ユーリ「そだね。ぜんぜん難しくない」

僕「……」

ユーリ「難しくないよね？」

僕「うん、そうだね」

ユーリ「何考えてたのん？」

僕「$(a - b)/2$ は、 $(a + (-b))/2$ だなあって考えてた」

$$ \frac{a - b}{2} = \frac{a + (-b)}{2} $$

ユーリ「そーだけど……それって、物語の重大な伏線になってるの？　 覚えとくと後で感動やってくるの？　メモした方いい？」

僕「いや、伏線とかそういうんじゃないよ。 それにそこまで突っ込まれると伏線だとしても台無しだな！」

ユーリ「へへ。じゃれてるだけじゃん。あー楽しい」

$(a + b)/2$ を作る

僕「次は $a, b$ から $(a + b)/2$ を作る」

ユーリ「さっきと同じだよね。ここが $a + b$ になるから、また垂直二等分線作ればいい」

$\SQRT{ab}$ を作る

僕「これで $(a - b)/2$ と $(a + b)/2$ の作図はできたことになるから、 いよいよ $\SQRT{ab}$ の作図に掛かる」

ユーリ「これが正方形の一辺になるんでしょ？」

僕「そうだね。 $B = (a - b)/2$ として、 $C = (a + b)/2$ としたとき、 $B$ がひとつの辺で、 $C$ が斜辺になるような直角三角形を描くんだ」