![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ユーリと僕は、 オームの法則や(第332回参照)、 クーロンの法則や(第333回参照)、 コンデンサの仕組みや(第334回参照)、 キルヒホッフの法則についておしゃべりしていた(第335回参照)。
ちょうど、クイズを解いたところ。
僕「……ところでさっきのクイズの答えは、こうだったね」
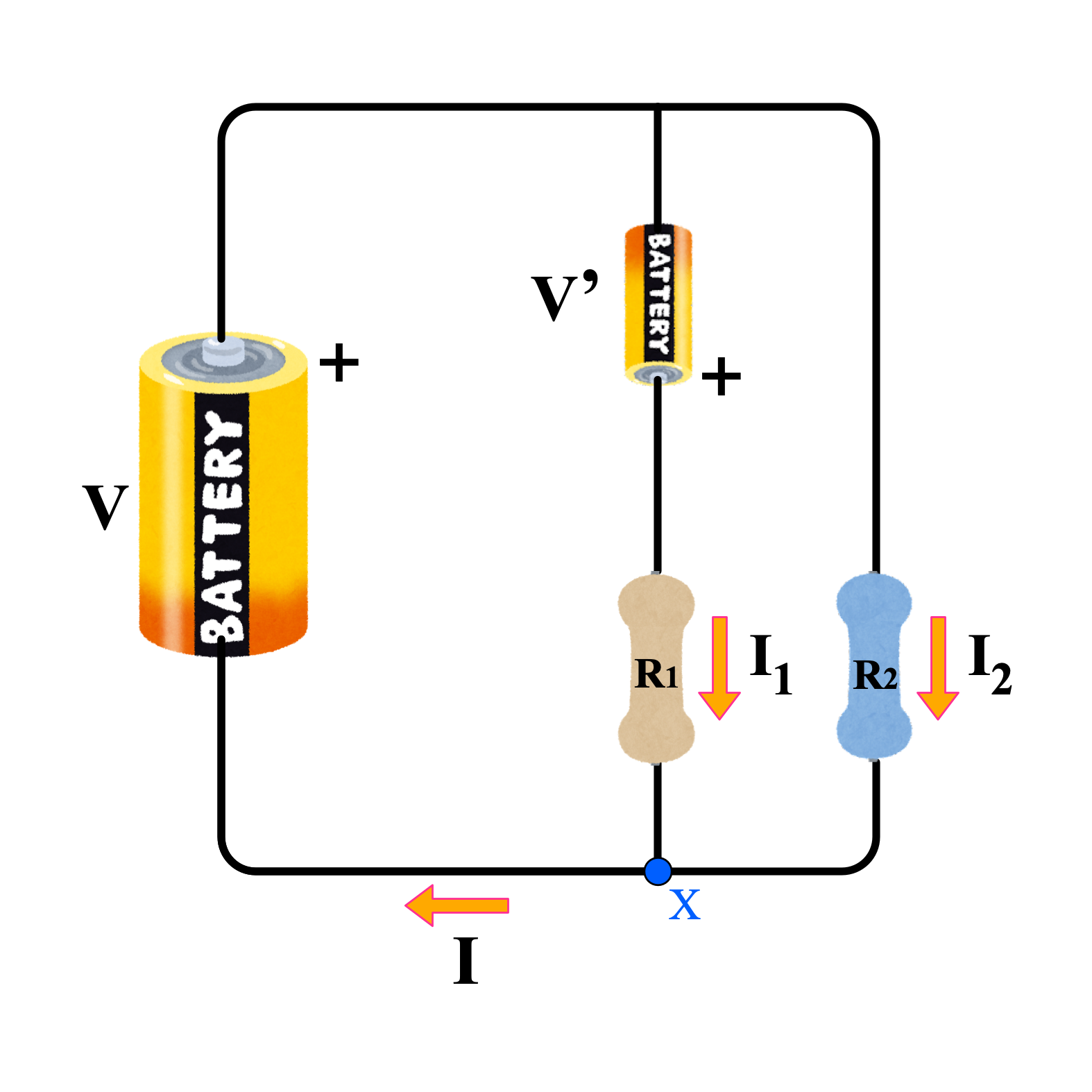
$$ \begin{align*} I &= I_1 + I_2 \\ &= (V + V')/R_1 + V/R_2 \\ \end{align*} $$
ユーリ「うん」
僕「この式を少し変形してみる」
$$ \begin{align*} I &= (V + V')/R_1 + V/R_2 \\ &= V/R_1 + V'/R_1 + V/R_2 \\ &= (1/R_1 + 1/R_2)V + V'/R_1 \\ \end{align*} $$ユーリ「$V$ でくくった?」
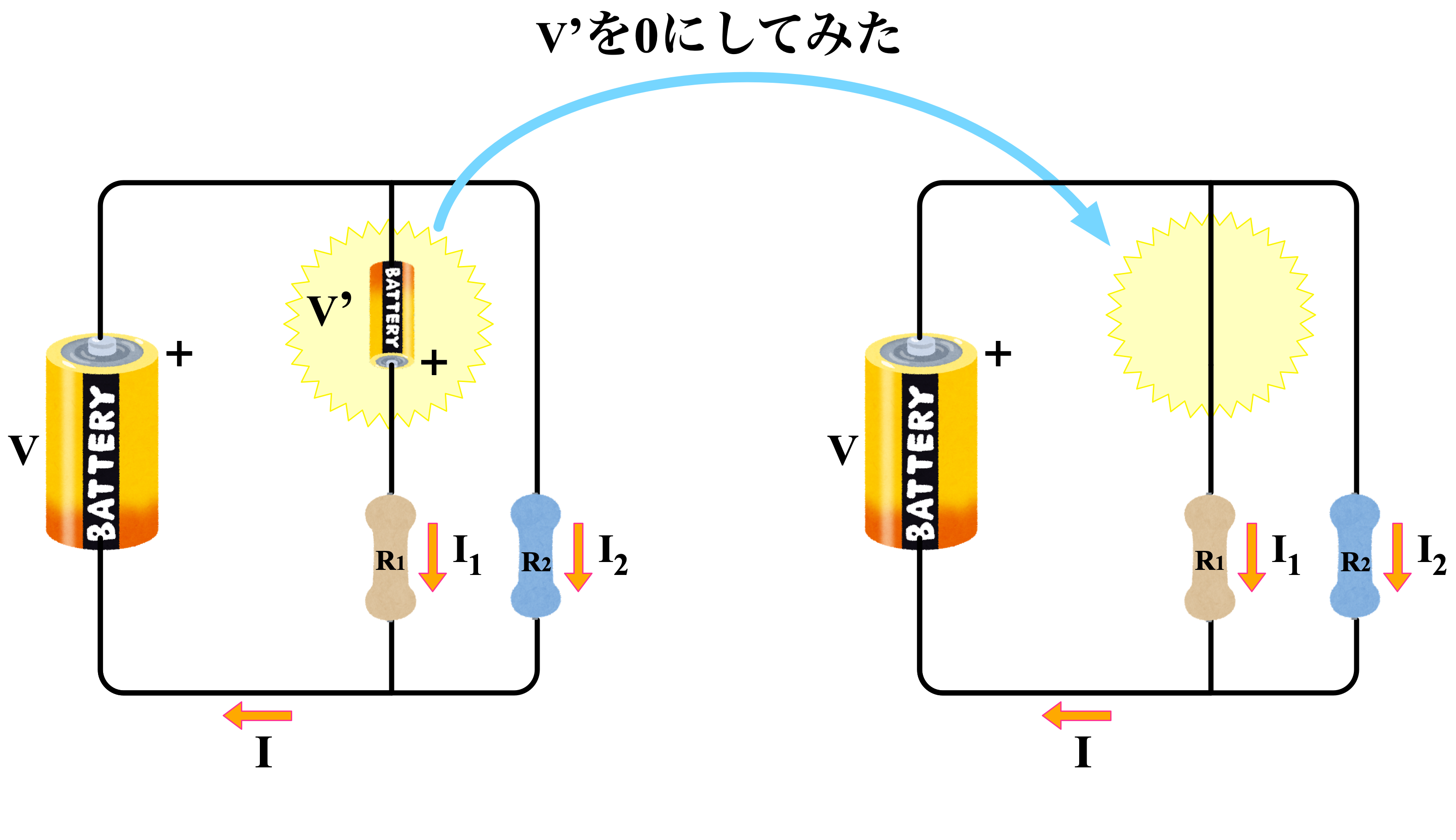
僕「そうだね。そしてこの式をよく見て、ユーリがさっき『邪魔だ』って言った $V'$ をゼロにしてみよう。どうなる?」
ユーリ「電圧をゼロにする……こーゆーこと?」
$$ I = (1/R_1 + 1/R_2)V $$僕「そうそう。それで、これはちゃんと、 $R_1,R_2$ の並列つなぎになっているよね。 だって、合成抵抗を $R$ としたとき、こうなるから(第332回参照)」
$$ I = (1/R)V $$ユーリ「?」
僕「クイズで出した回路で $V' = 0$ にしたなら、単なる抵抗の並列つなぎになる。だとしたら《式の形》でも、ちゃんと並列つなぎの式になるはずだなあと思ったんだ。 そして、ちゃんとそうなっている。だから、途中で計算ミスをしている可能性は低いな、と思ったんだよ」
$V' = 0$ にしてみた
ユーリ「そんなことしていーんだ」
僕「だって、 $V'$ のように文字を使うのは、そのためだよね。 値を変化させて、おもしろいことは起きないか、みたいな。 文字にいろんな値を入れてみて、どういう変化をするか、とかね」
ユーリ「ほほー。む、ちょっと待った! もしも $I = (1/R)V$ で……」
僕「うん」
ユーリ「抵抗をゼロにすることにしたら? $R = 0$ にしたらどーなんの? 電流が無限大?!」
僕「ああ、それを考えていたのか。Rが分母にあるから、ゼロにするのはまずいね。ゼロ割になってしまう」
ユーリ「違うの、違うの。完全にゼロにしなくても、Rをものすごーく小さくするんだよー! そしたらIはものすごーく大きくなるよね?」
$$ I = V/R $$僕「そうだね。たとえば、この回路でRをすごく小さくするということは、電気抵抗の大きさを小さくしているわけだから、 電流が大きくなる。それは正しいよ」
ユーリ「それ、やばいよね。だって、Rはいくらでも小さくできるから、Iはいくらでも大きくなる」
僕「うん。それはそう。でも、現実の回路では、そうはならないし、そうはできないんだ」
ユーリ「え、なんで?」
僕「理由はいくつかあるよ。まず、電気抵抗Rをゼロに近付けるのには限界がある。金属の中を自由電子が移動するときには、 どうしても抵抗が発生してしまう。物体を極端に冷却して《超伝導》の状態を考えればまた話は違うけれど」
ユーリ「超伝導、聞いたことある。QuizKnockのナイスガイ須貝さんが研究してる」
僕「そうそう」
ユーリ「抵抗はゼロにできなくても、抵抗をなくしちゃったら?」
僕「それは、電池をショートさせるってことだね。それはとっても危険!」
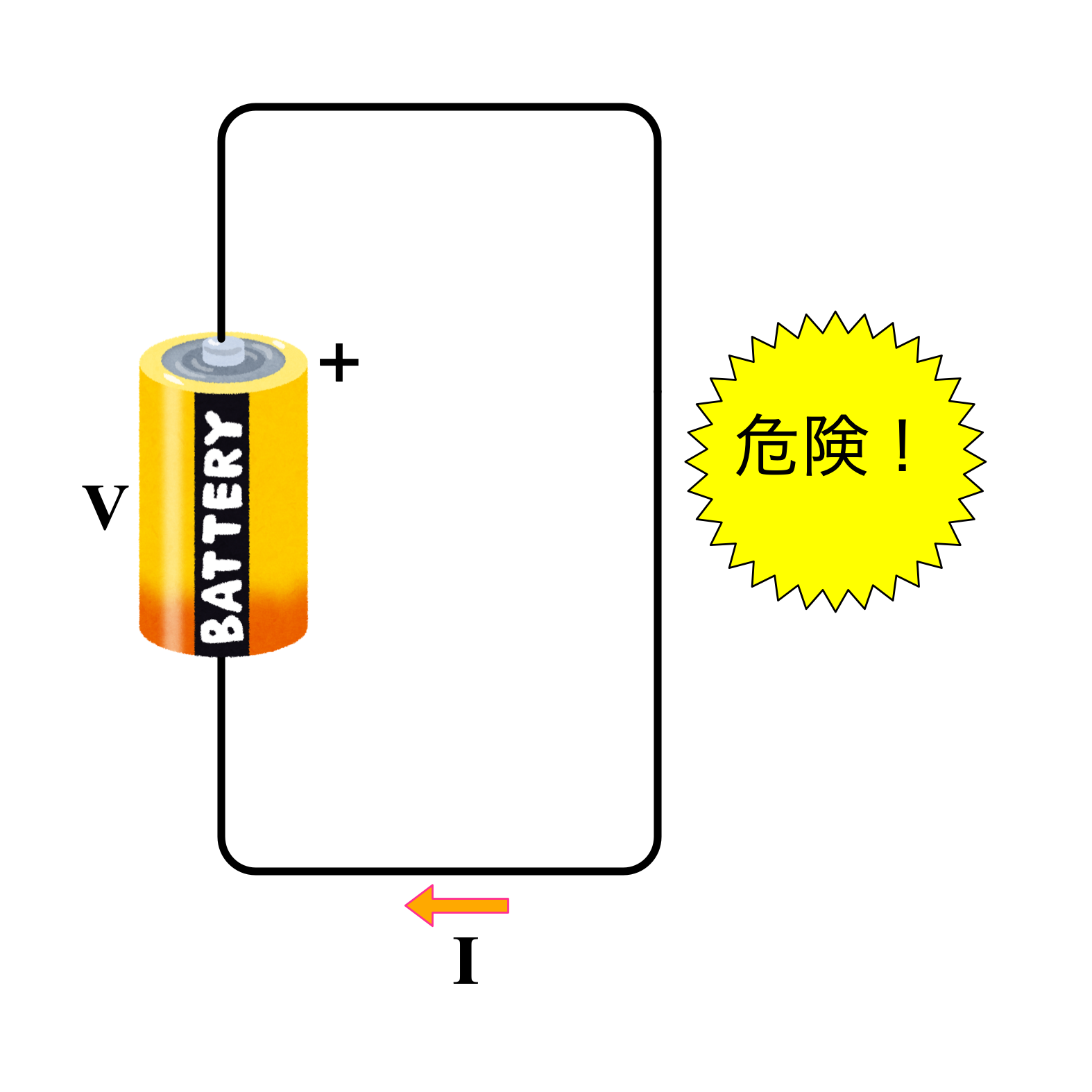
ユーリ「危険?」
僕「ものすごく大きな電流が流れるから、高温になってやけどしたり、発火したりすることがある」
ユーリ「あー、やっぱり電流は大きくなるんだ」
僕「そうだね。それはそう。でもいくらでも大きくなるわけじゃない。 電池が自由電子を運ぶ働きは無限大じゃないから、電圧がキープできなくなるんだ」
ユーリ「電圧がキープできない? どーゆーこっちゃ」
僕「抵抗を小さくすると、流れる電流は大きくなる」
ユーリ「それはわかる」
僕「抵抗をとても小さくして、電流がとても大きくなると、電圧が小さくなるんだ」
ユーリ「は? そんなの、 $I = V/R$ から言えんの?」
僕「言えない。 $I = V/R$ というのはオームの法則だよね。 電流が大きくなると電圧が小さくなるというのは、電池の性質から来るものだよ」
ユーリ「電池の性質って、電圧を作る? えーと、電位差? 起電力だっけ?」
僕「うん。順を追って話そう」
ユーリ「おっけー」
僕「電池は化学的な反応を使って、プラス極とマイナス極のあいだに電位差(でんいさ)を作る」
ユーリ「うん。1.5ボルトとか」
僕「そうだね。乾電池の1.5ボルトというのは、 プラス極とマイナス極のあいだの電位差の大きさを表している。 電流が流れていないとき、 この電位差のことを電池の起電力(きでんりょく)という」
ユーリ「お? いま、なにげに条件つけたね?」
僕「よく気付いたね」
ユーリ「ふふん。ユーリさまは条件を聞き逃すことはないのさっ!」
僕「すごいな」
ユーリ「《電流が流れていないとき》とわざわざ断ってたじゃん?」
僕「そう。今回の話のポイントはそこにある。 電流が流れていないとき、プラス極とマイナス極のあいだ……つまり電極間の電位差を起電力という」
ユーリ「てことは、電流が流れているときは違う?」
僕「そうなんだ。微妙な話になるから、 電極間の電位差のことを《端子電圧》(たんしでんあつ)とよぶことにしよう。 そうすると、電流が流れていないときには《端子電圧》と電池の《起電力》は等しい」
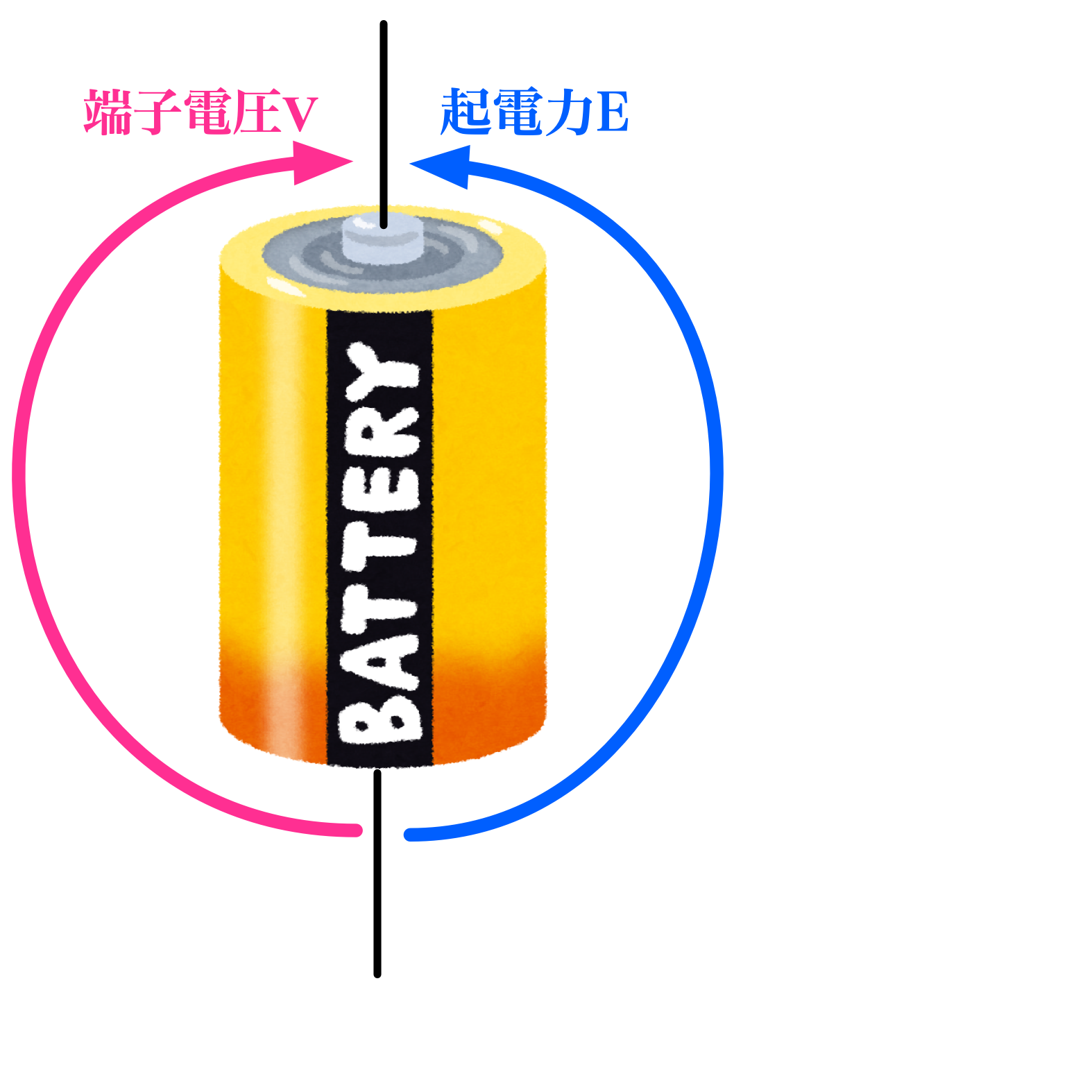
ユーリ「……」
僕「電流を流すと、電池の《端子電圧》は下がっていくんだ。これは電池が持っている性質。 大きな電流を流せば流すほど、《端子電圧》は下がる」
ユーリ「たくさん電流を流すと、《端子電圧》……電池のプラス極とマイナス極の間の電位差が小さくなるってこと?」
僕「そういうこと。現実世界の電池は、無限に大きな働きができるわけじゃないんだね」
ユーリ「ふーん」
僕「ところで、《起電力》と《端子電圧》と分けて考えるとおもしろいことがわかる」
ユーリ「おもしろいこと?」
僕「そうだよ。『電流がたくさん流れると《端子電圧》が下がる』というのを、 こんな仮想的な回路で説明することができるんだ」
↓↓↓
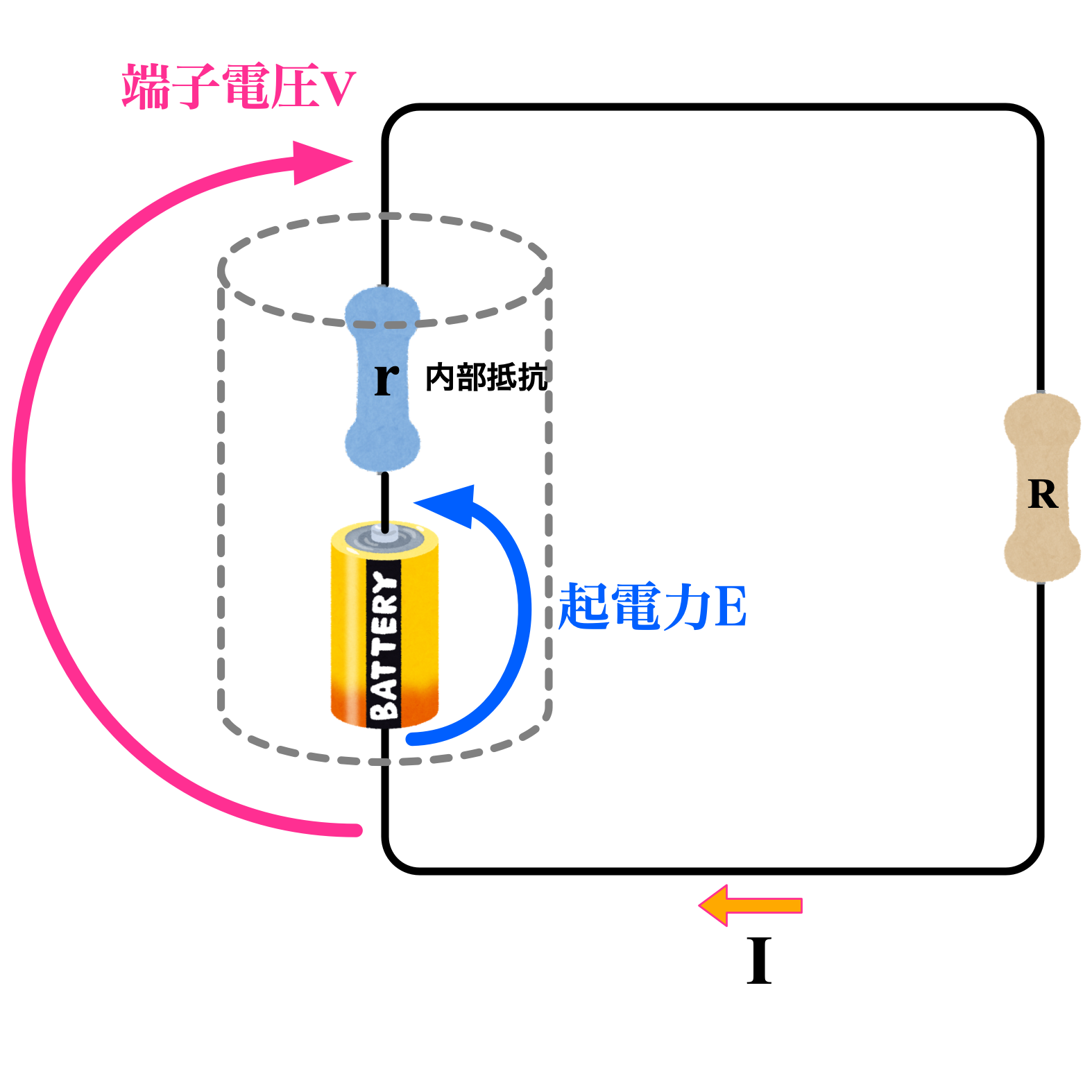
ユーリ「何これ。大きな電池の中に小さな電池が入ってる?」
僕「電池の絵の内部に描いた電池は《起電力》を表現する。起電力は電位差Eを作り出すものとする。 そして、いくら大きな電流が流れてもEの値は変化しないとする」
ユーリ「んー、理想の電池みたいなもん?」
僕「そう考えてもいいよ。そして、小さな電池の上に抵抗を描いた。これは、仮想的に、電池の内部にあると考えた抵抗で、内部抵抗(ないぶていこう)と呼んでいる。 そして《端子電圧》をVとする。Vが僕たちに見える外側の電池が作り出す電位差だね」
ユーリ「ちょっと待ってよ。話をややこしくしてる?」
僕「してない、してない」
ユーリ「じゃ、何やってるの?」
僕「『電池に電流を流すと《端子電圧》が下がる』という電池の性質をうまく説明するモデルの話をしてるんだ」
ユーリ「うーん……」
僕「もうちょっと話が進むと『にゃるほど』になるよ」
ユーリ「お兄ちゃんの猫語、へんだよ」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 430本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2021年9月24日)