![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
いまは土曜日。
ここは僕の部屋。
僕とユーリはいつものように数学のおしゃべりをしている。
ユーリがノナに三角関数を教えようとしたという話題に始まって、 $\cos, \sin, \tan$ について話していた。
いまはちょうど、 $$ \tan{\theta}\tan(\KAKUDO{90} - \theta) = 1 $$ の証明が終わったところ(第311回参照)。
ユーリ「ほらね! ユーリは三角関数カンペキでしょ? お兄ちゃんの出す問題なんか、全部わかっちゃうよ!」
僕「そりゃすごいな。 でも確かにユーリは、 $\tan$ の定義もちゃんとわかっているし、 $\tan\KAKUDO{30}, \tan\KAKUDO{45}, \tan{\KAKUDO{60}}$ の値も、きちんと考えているよね」
ユーリ「ふふん。単位円を描けばすぐわかるもん。三角関数カンペキさ!」
僕「じゃあ、ちょっと違うクイズを出してみようか」
ユーリ「どんとこい」
僕「ユーリは $\cos,\sin,\tan$ を三角関数だって言ってたよね。 関数というからには定義域は何だろう」
ユーリ「わかんない」
僕「がく」
ユーリ「あっ、ちがうちがう。答えがわかんないんじゃなくて、お兄ちゃんが何を言ってるかがわかんないの!」
僕「関数っていうのは、数を何か与えると、数が得られるものだよね。まあ、数じゃないこともあるけど」
ユーリ「えーと?」
僕「うん、じゃあ、たとえば、関数 $\cos$ で具体的に話そうか。 角度 $\theta$ を $\cos$ という関数に与えると、数 $\theta$ に対応して単位円上の点の $x$ 座標という数が得られるよね。 いま角度は《度》で考えているから、 $\cos$ に $60$ を与えると、 $0.5$ が得られるという具合に」
関数 $\cos$ に $60$ を与えると $0.5$ が得られる

※角度は《度》で考えています。
ユーリ「それって、 $\cos\theta$ の定義の話、してる?」
僕「そうだよ」
ユーリ「$\cos$ に $\KAKUDO{60}$ を与えると $\frac12$ だから $0.5$ が得られるって?」
関数 $\cos$ に $\theta$ を与えると $x$ 座標の値が得られる

僕「そうそう、そういう話。 そのとき、いま考えている関数 $\cos\theta$ では、 $\theta$ として与えることができるのは実数だよね」
ユーリ「そだね。数だから」
僕「数といってもいろいろある。たとえば $\theta$ に虚数の $i$ を与えることは、いまは考えていない。考えているのは実数だけ」
ユーリ「ほほー。虚数の角度?」
僕「$\theta$ を虚数にするという話は、それはそれでおもしろい話につながるけど、いまは実数だけを考えている」
ユーリ「そんで? お兄ちゃんは何が言いたいの?」
僕「関数を考えるときには《その関数に与えることができるのはどんな数なのか》をきちんと決めておく必要があるという話だよ。 $\cos\theta$ の $\theta$ に対して $\KAKUDO{0}$ を与えてもいいし、 $\KAKUDO{30}$ を与えてもいいし、もっと大きな数やもっと小さな数を与えてもいい。 $\KAKUDO{100}$ とか $\KAKUDO{360}$ とかね」
ユーリ「$\KAKUDO{3000}$ とか」
僕「そうだね。それからマイナスでもいい。 $-\KAKUDO{60}$ とかね」
ユーリ「いーよ」
僕「つまり、僕たちはいま $\cos\theta$ という関数の定義域を、実数全体の集合だと考えているわけだ」
ユーリ「てーぎいき」
僕「そう。 $\cos$ という関数に与えることができる数全体の集合を、関数 $\cos$ の定義域という。 いま僕たちは、関数 $\cos\theta$ の定義域を実数全体の集合だとして考えていることになる」
ユーリ「ねえ……お兄ちゃん。それって簡単な話をややこしく言ってる?」
僕「そうじゃないよ。簡単な話を正確に言ってるんだ」
ユーリ「はいはい」
僕「ユーリは《実数全体の集合》といわれて、ピンと来てるよね?」
ユーリ「だいじょーぶ。数直線でしょ?」
僕「うん、それでいいよ。 数直線は実数全体の集合だと考えることができるし、 一つ一つの実数は数直線上の点として考えることができる。 実数全体の集合のことは $\REAL$ と書くこともある」
ユーリ「はいはい。そんでそんで?」
僕「それが $\cos\theta$ の定義域。 それに対して、 $\cos\theta$ の値域というものもある」
ユーリ「ちいき」
僕「そう。関数 $\cos\theta$ がとる値全体の集合のことを $\cos\theta$ の値域という。 $\cos\theta$ の値域って、具体的に何だかわかる?」
ユーリ「わかんない」
僕「がく。『そのスピードは考えていない証拠』ってミルカさんに言われたことなかったっけ?」
ユーリ「ぐぬぬ。ミルカさまを出してくるなー!」
僕「$\cos\theta$ の値域って、具体的に何だかわかる?」
ユーリ「えーと? ……結局 $\cos\theta$ って、点の $x$ 座標だよね?」
僕「そうだね。 $\cos\theta$ の定義から、 単位円の円周上にある点の $x$ 座標だといえる」
ユーリ「だったらカンタン! ぐるっと回るから、 $-1$ から $1$ までの範囲だ。 こーゆーこと!」
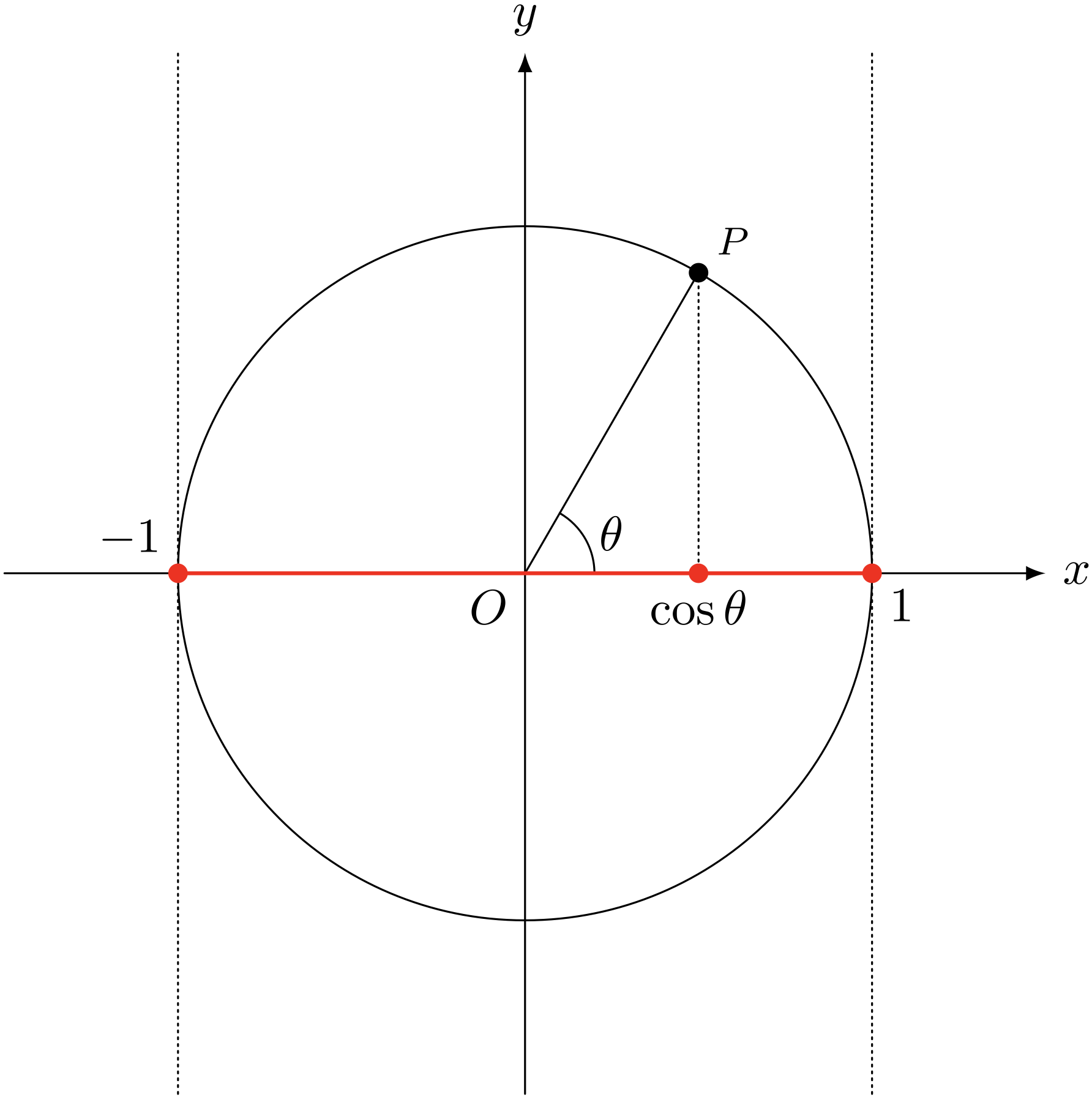
僕「そうだね。ユーリはちゃんとわかってる。 関数 $\cos\theta$ の値域は《$-1$ 以上で $1$ 以下の実数全体の集合》になる。 関数 $\cos$ の値域は、数式を使ってこんなふうに書くこともできる」
$$ \SET{x \SETM -1 \LEQ x \LEQ 1 } $$ユーリ「あ、そーゆーの見たことある。お兄ちゃん、よく書くよね」
僕「そうだね。 $x \in \REAL$ と書いて、実数であることをはっきりと書いてもいい」
$$ \SET{x \in \REAL \SETM -1 \LEQ x \LEQ 1 } $$ユーリ「いろんな書き方あるんだね」
僕「関数を考えるときには、もう一つ、終域(しゅういき)という集合を考えることがあるけれど、それはまた今度話をしよう」
ユーリ「いま一瞬、テトラさんが見えたよ」
僕「それはさておき、定義域と値域のクイズを出そう。いいよね」
ユーリ「いいよん。理解したから大丈夫!」
僕「僕たちが考えている関数 $\cos\theta$ の定義域は《実数全体の集合 $\REAL$》で、 値域は《$-1$ 以上 $1$ 以下の実数全体の集合》だったよね」
ユーリ「それ、さっきやった」
僕「それじゃ今度は、関数 $\sin\theta$ の定義域と値域は?」

無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2021年1月15日)