第313回シーズン32 エピソード3

ふれあう三角関数：タンジェントをなぞって（前編）

登場人物紹介

僕：数学が好きな高校生。

ユーリ：僕のいとこの中学生。僕のことを《お兄ちゃん》と呼ぶ。論理的な話は好きだが飽きっぽい。

$ \newcommand{\ABS}[1]{\left|\mathstrut #1\right|} \newcommand{\KAKUDO}[1]{#1^\circ} \newcommand{\TT}[1]{\textrm{#1}} \newcommand{\ANGLE}[1]{\angle\textrm{#1}} \newcommand{\TRI}[1]{\triangle\textrm{#1}} \newcommand{\SQRT}[1]{\sqrt{\mathstrut #1}} \newcommand{\TRUE}{\textbf{true}} \newcommand{\FALSE}{\textbf{false}} \newcommand{\FOCUS}[1]{\fbox{ $#1$ }} \newcommand{\GEQ}{\geqq} \newcommand{\LEQ}{\leqq} \newcommand{\NEQ}{\neq} \newcommand{\TRIANGLE}{\triangle} \newcommand{\REMTEXT}[1]{\textbf{#1}} \newcommand{\PS}[1]{\left(#1\right)} \newcommand{\SET}[1]{\{\,#1\,\}} \newcommand{\SETM}{\,|\,} \newcommand{\EMPTYSET}{\{\,\}} \newcommand{\REAL}{\mathbb R} \newcommand{\ZEE}{\mathbb Z} $

僕の部屋

僕とユーリは、分度器と定規を使って、 $y = \tan\theta$ のグラフを描いていた（第312回参照）。

描いたグラフはまだ $\KAKUDO{0} < \theta < \KAKUDO{90}$ の範囲だけど、それでもなかなか楽しいぞ。

単位円と $y = \tan\theta$ のグラフ（$\KAKUDO{0} < \theta < \KAKUDO{90}$）

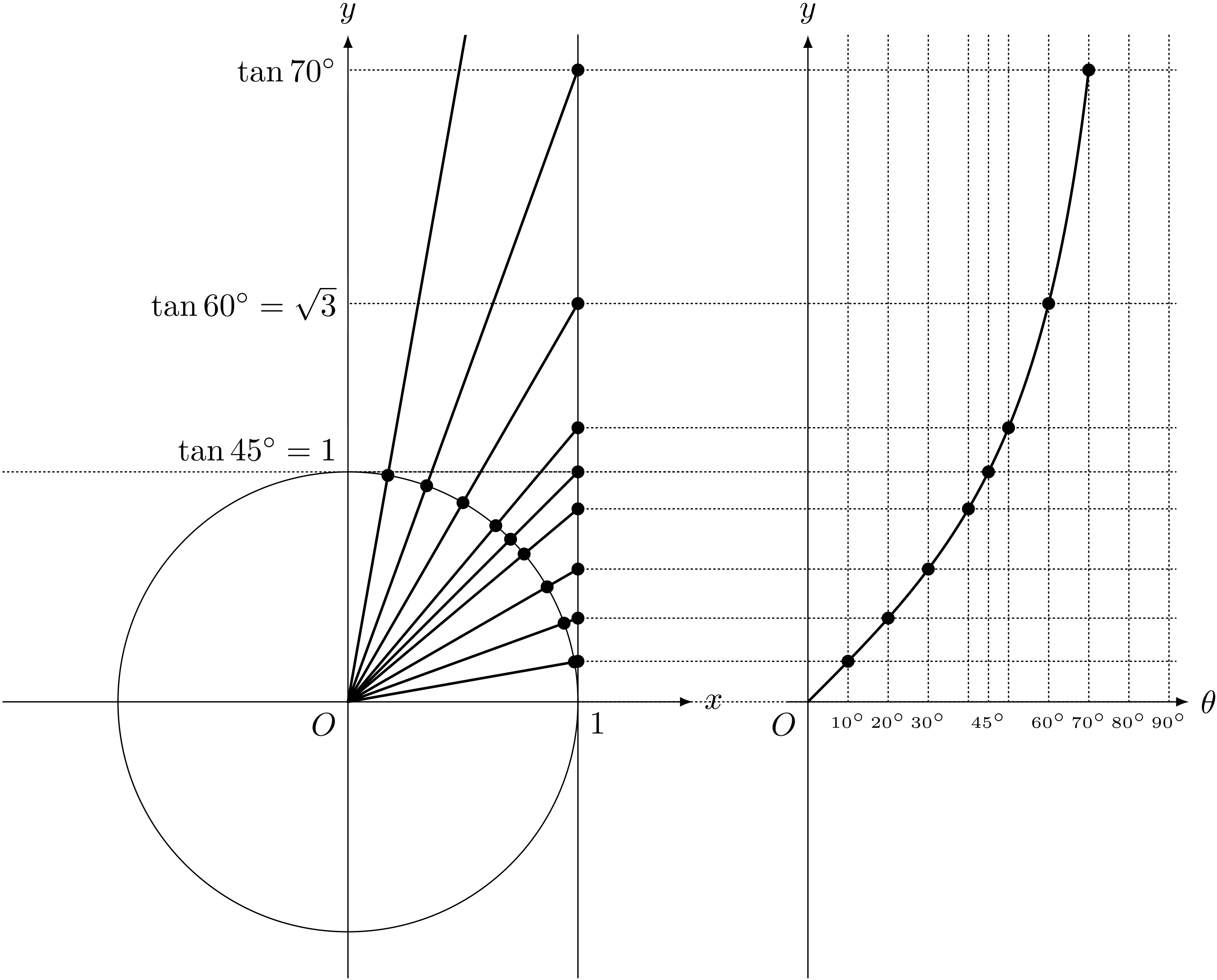
ユーリ「うんうん、予想どーり！　90度に近づくと、ぎゅーんと増えてく！」

僕「そうだね。タンジェントは、 $$ \tan \theta = \frac{\sin\theta}{\cos\theta} $$ で定義されている。 $\theta$ の値が0度から90度に近づいていくと、 $\cos$ の値は1から0に向かって小さくなる。分数の分母が0に近づくから、 $\tan$ の値はものすごく大きくなっていくわけだよね」

ユーリ「90度だとゼロ割が起きちゃうから、そこは《なし》でいーんでしょ？」

僕「うん。 $\cos$ の値が0になるところは $\tan$ の定義域には含まれていないから、グラフには描けないよ。もっとも、90度になるずっと手前で、グラフとしては描けなくなっちゃうけどね。上にはみ出しちゃうから」

僕はそういいながら、ノナのことをふと思い出した（『数学ガールの秘密ノート／学ぶための対話』参照）。

最初のうちは、意味を考えることがピンと来ていなかったノナだけど、具体的なグラフ上の点についてはすぐに理解していた。

それから、グラフには描けないけれど、ずっとずっと遠くの方まで続いていることも。

そうこうしているうちに、大事なものをつかんだ瞬間があった。

あれは、確か……

90度を越したらどうなる？

ユーリ「ねー、お兄ちゃん。90度を越したらどーなんの？」

僕「どうなるの、とは？」

ユーリ「ほら、90度だと点Pが原点Oの真上にくるから、交点Qがなくなるじゃん？」

$\theta = \KAKUDO{90}$ では交点 $Q$ がなくなる

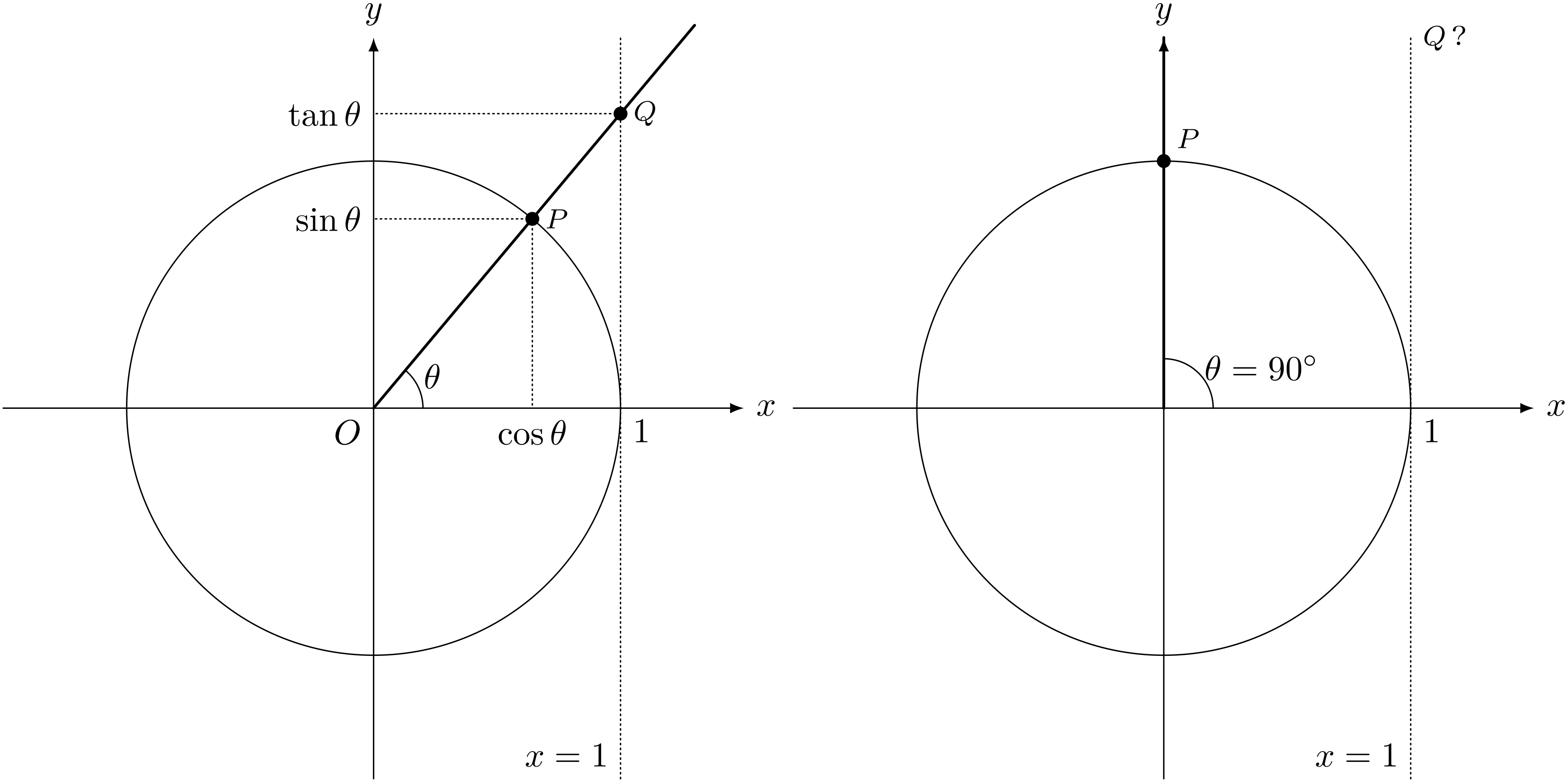
僕「そうだね。平行になるから」

ユーリ「90度を越しても、交点Qは作れないじゃん？」

$\theta > \KAKUDO{90}$ でも交点 $Q$ は作れない？

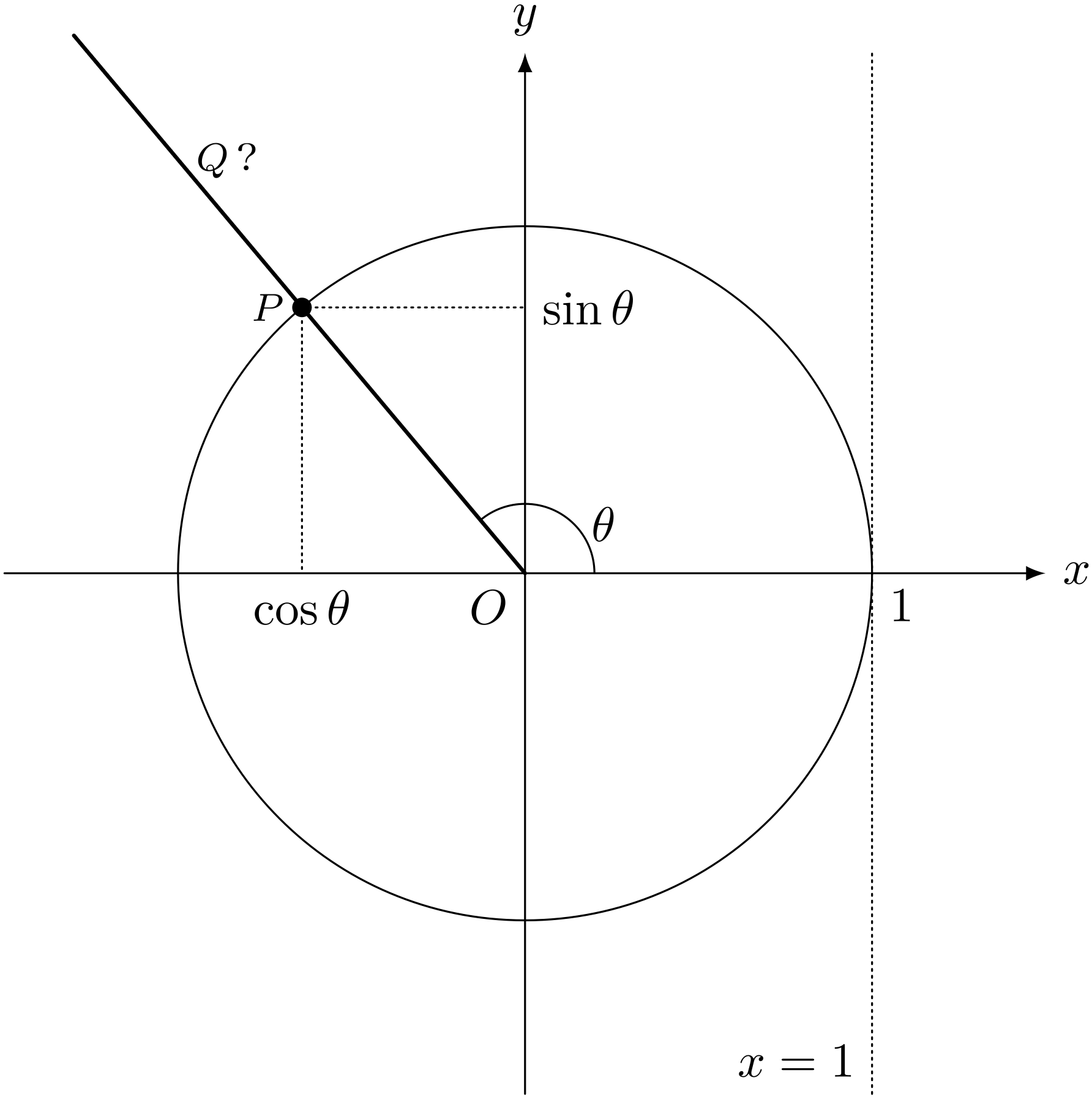
僕「いやいや、交点Qはこっちにあるよ」

$\theta > \KAKUDO{90}$ での交点 $Q$

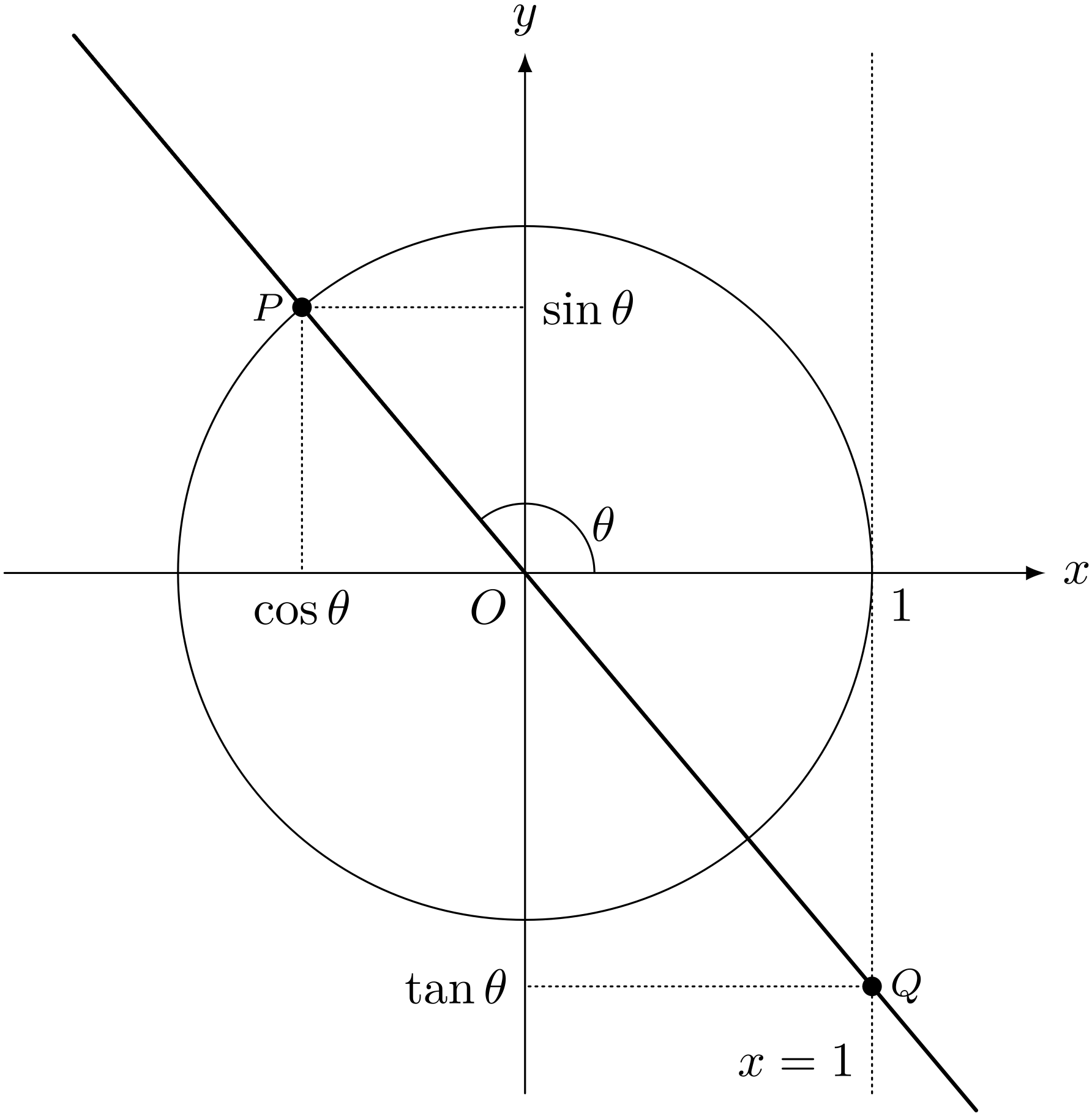
ユーリ「あーなるほど……え？　それでいーの？　だって、半直線OPと直線 $x=1$ との交点じゃなかったっけ」

僕「ああ、そうだね。半直線OPという表現はよくなかったかもしれない。原点OとPとを結ぶ直線と直線 $x = 1$ の交点をQとしたほうが正確だね」

ユーリ「うーん……ほんとにこの点Qのy座標が $\tan\theta$ なのー？」

僕「確かめたかったら、また《定義にかえれ》を使えばいいよね」

ユーリ「またかい」

僕「だって、『$\tan\theta$ とは何か』を定めているのが定義なんだから、そこをしっかり足場にしなかったら、何をやってるかわからなくなっちゃうよね」

ユーリ「へいへい。 $\tan$ の定義は、 $$ \tan\theta = \frac{\sin\theta}{\cos\theta} $$ ですよっと。それで……」

そこでユーリは、真面目な顔になって考え始めた。

点Qのy座標が本当に $\tan\theta$ になっていることを確かめているのだ。

直線 $OP$ と直線 $x = 1$ との交点 $Q$ の $y$ 座標は本当に $\tan\theta$ なのか？

僕「……どうかな？」

ユーリ「$\tan$ の定義を考えるんだから、こことこことを考えるんだよね？」

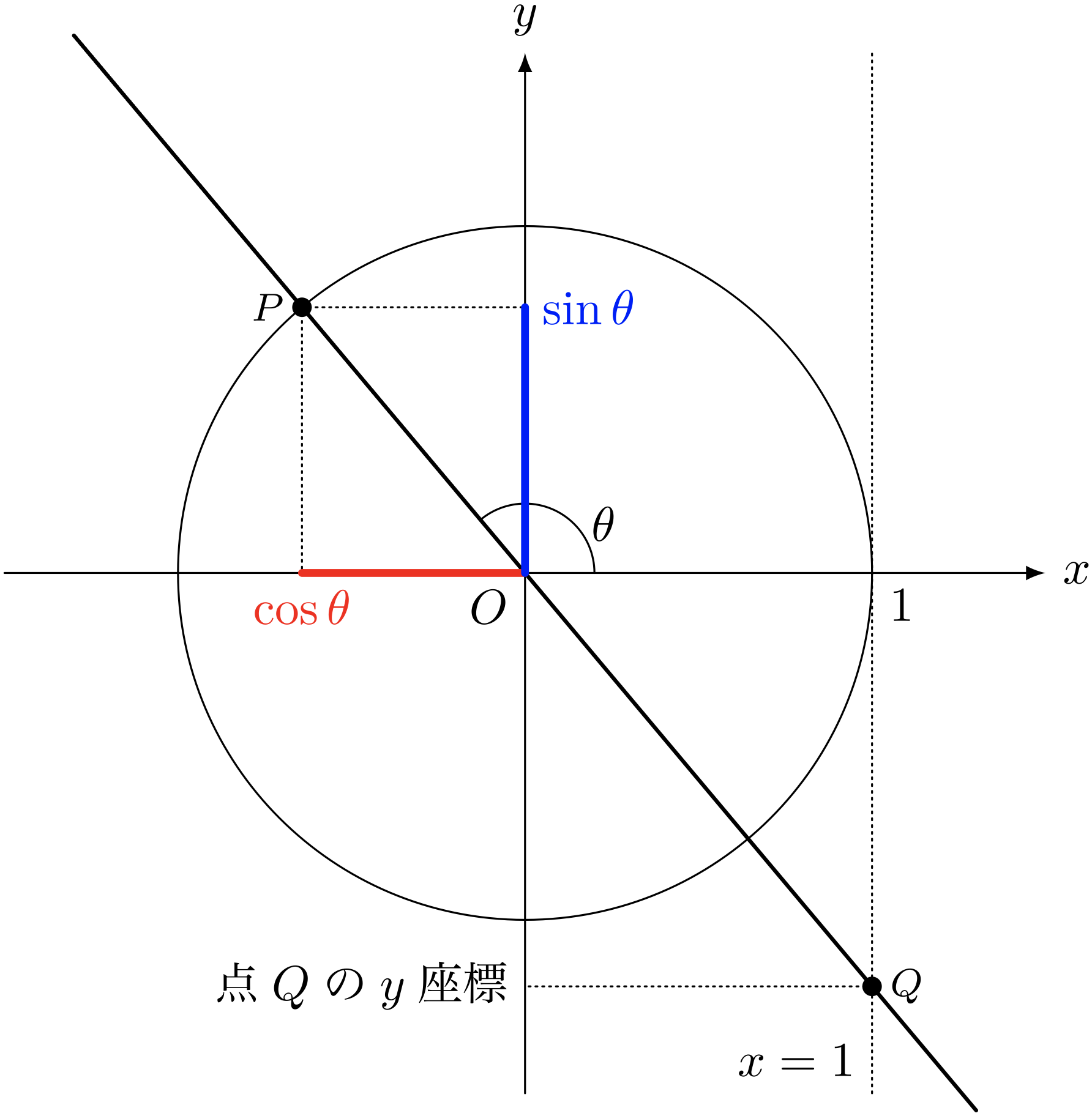
僕「そうだね。この長さは……」

ユーリ「待って待って！　三角形でしょ？　またこれも三角形の相似を使えばいいんだね！」

ユーリ「二つの三角形が相似だから、 $$ \frac{\sin\theta}{\cos\theta} = \frac{\REMTEXT{点$Q$の$y$座標}}{1} $$ になって、 $$ \tan\theta = \REMTEXT{点$Q$の$y$座標} $$ だ！」

僕「それでいいね」

ユーリ「でも、プラスマイナスがおかしくね？」

僕「いやいや、おかしくないよ」

ユーリ「でも、点Qのy座標はマイナスだし……」

僕「だって点Pの位置を考えると、 $$ \begin{align*} \cos\theta &< 0 \\ \sin\theta &> 0 \end{align*} $$ で正負が異なるから、 $\tan$ つまり割り算の結果はマイナス。点Qのy座標もマイナス。さっきユーリが書いた等式、 $$ \frac{\sin\theta}{\cos\theta} = \frac{\REMTEXT{点$Q$の$y$座標}}{1} $$ は両辺ともマイナスになっていて、正しい。三角形の辺の長さという意味では、絶対値を取って、 $$ \frac{\ABS{\sin\theta}}{\ABS{\cos\theta}} = \frac{\ABS{\REMTEXT{点$Q$の$y$座標}}}{1} $$ ということになるけどね」

ユーリ「あっ、わかった。勘違い、勘違い。もーわかったよー」

僕「どんな勘違いをしたんだろう？」

ユーリ「いやー《ほんのちょっとしたこと》だからいーよ。プラスマイナスの勘違いってこと！」

僕「それは、どんな勘違いなんだろう？」

ユーリ「出た出た《根掘り葉掘りお兄ちゃん》！」

僕「変な名前付けるなよ」

ユーリ「あのね、さっき、 $\tan$ の定義を、 $$ \tan \theta = \frac{\sin\theta}{\cos\theta} $$ って言ったけど、コサインがマイナスのときには、 $$ \tan \theta = \frac{\sin\theta}{-\cos\theta} \qquad \REMTEXT{（？）} $$ じゃね？　って思ったの。でも違うよね。錯覚、サッカク」

僕「なるほどなあ。うん、違うよ。 $\tan$ の定義は、 $$ \tan \theta = \frac{\sin\theta}{\cos\theta} $$ でいい。 $\cos\theta,\,\sin\theta$ の正負によらないね」

ユーリ「だよね」

僕「$\theta$ の値に応じて自動的に $\cos\theta,\sin\theta,\tan\theta$ の正負はそれぞれに決まる。いちいち式の方でプラスマイナスの記号を個別に付ける必要はない。便利なところだね」

ユーリ「は？　何が便利なの？」

僕「文字を含んだ式で書くと便利だという話」

ユーリ「んー……？」

僕「たとえば $0.5$ のような数で考えるのはわかりやすい。数直線ではここにあるとか、 $0$ より大きいとかいうイメージもとらえやすい」

ユーリ「そだね。具体的」

僕「それはそれでいいんだけど、文字や式を使って書くと、 $\theta$ がどんな値のときでも、たとえば、 $$ \cos\theta $$ という式は、点Pのx座標を表す。表し続けてくれる。それは考えを進める上ですごくありがたいと思わない？　 $\cos\theta$ がプラスだろうがゼロだろうがマイナスだろうが、安心して式変形できる。それは便利だよ」