![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ユーリ「ねーお兄ちゃん。相談があんだけど……」
僕「相談? ユーリ、どうした?」
僕は高校生。ここは僕の家。
中学生のいとこ、ユーリが遊びに来ている。
いつもなら軽口を飛ばしてくる彼女なのに、 今日は珍しく真面目な顔をしている。
ユーリ「あのね、ノナのこと」
僕「ノナちゃん?」
ノナというのは、ユーリと仲良しのクラスメートだ。
ときどき家にも遊びに来ることがある。彼女がどうかしたんだろうか。
ユーリ「あのね、コサインとかサインってあるじゃん? タンジェントも」
僕「$\cos, \sin, \tan$ のことだよね。三角関数」
ユーリ「それそれ。こないだ、ノナに三角関数の話をしてたの」
僕「へえ……」
ユーリ「木の高さを計算する話で、三角関数のことをちょっと言ったら、ノナが知りたがったから」
僕「木の高さで三角関数……それは $\tan$ を使う話かな」
ユーリ「うん、そーなんだけど、話聞いてよ」
僕「はいはい、それで?」
ユーリ「ノナが三角関数のことを知りたがったから、コサインとサインを説明したの。 でも、ノナにさっぱり伝わらなかった。なんで? 三角関数ってそんなに難しくないよね?」
僕「コサインとサインを説明したっていうのは、定義を話したってこと?」
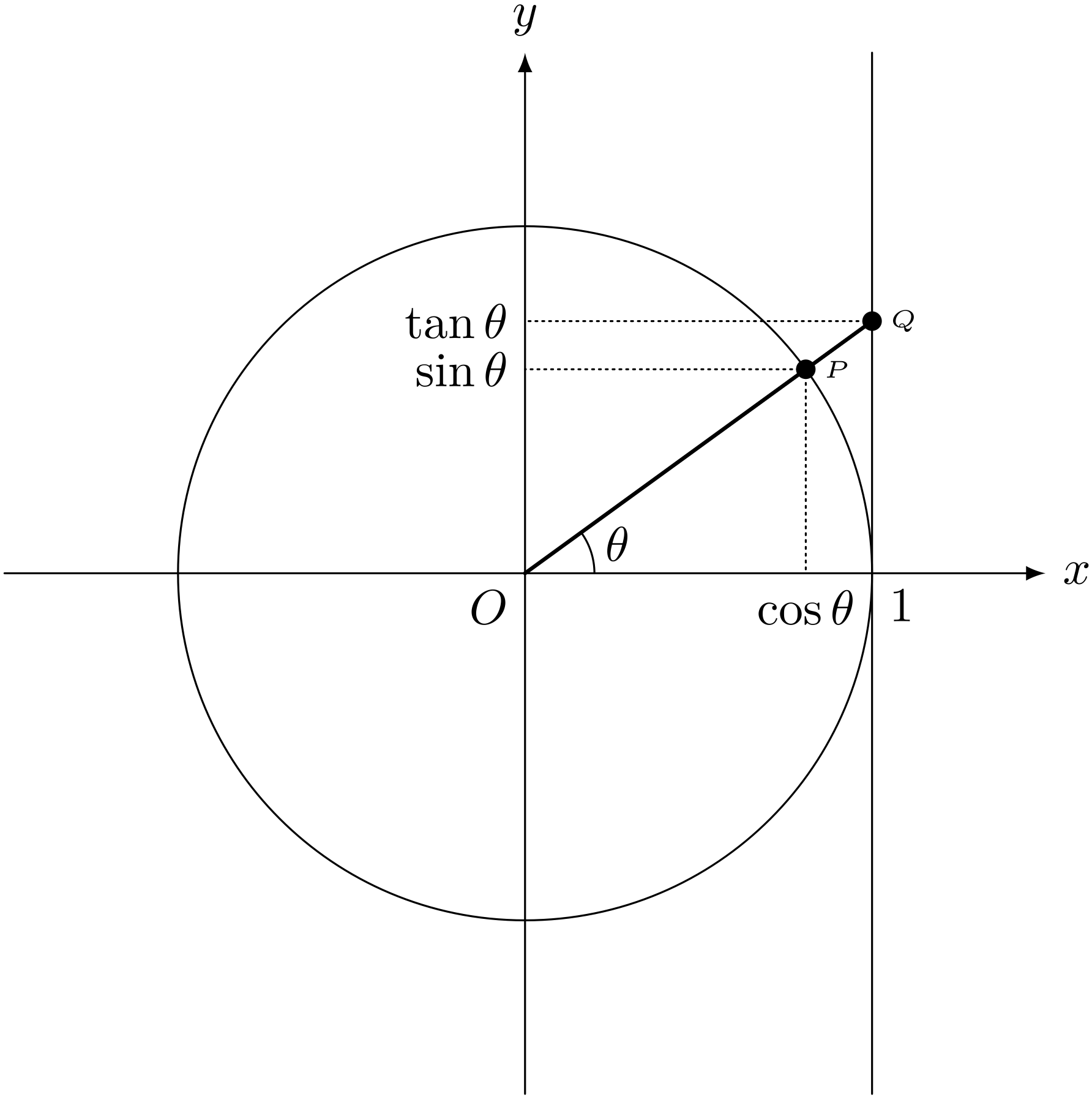
ユーリ「そだよん。ほら、お兄ちゃんがよく話すやつじゃん。 半径が1の円を描いて、円周上の点 $P$ を決めて、ここの角度を $\theta$(シータ)って呼んで……」
$\cos$ と $\sin$
座標平面上、原点 $O$ を中心として半径 $1$ の円を描く。
円周上の点を $P$ として、図のように線分 $OP$ と $x$ 軸とのなす角を $\theta$ とする。
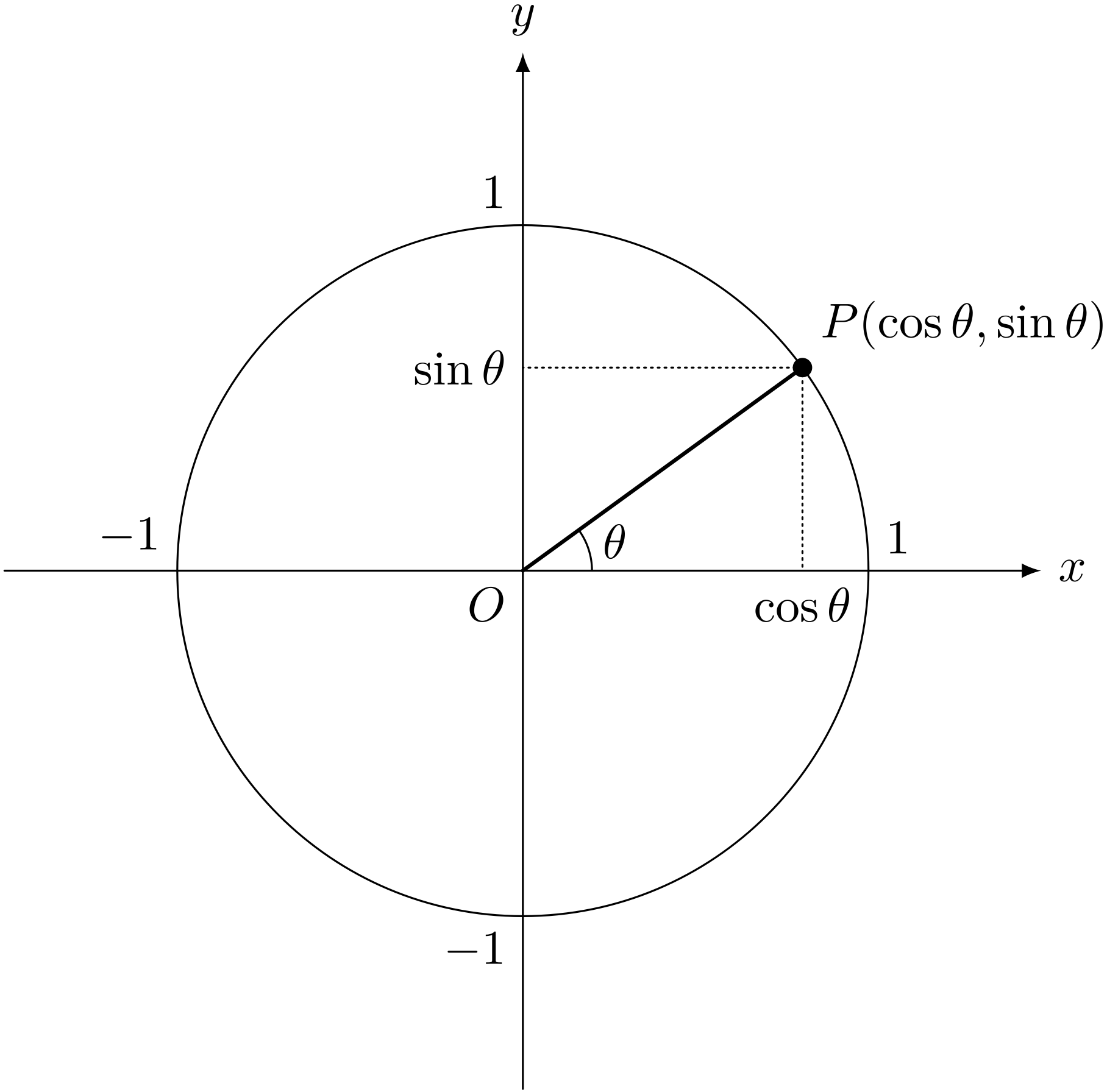
僕「うん、それは正しい定義だよ。 座標平面上、原点が中心で半径が $1$ の円。 単位円だ。その単位円を使って $\cos, \sin$ を定義する。 それがうまく伝わらなかったってこと? ノナちゃんは何て言ってたの?」
ユーリ「え?」
僕「え?」
ユーリ「ノナが何て言ってたか……?」
僕「定義を教えたんだよね。ユーリが教えた後、ノナちゃんは何か言ってたんじゃないの? それがわからないと、 どこまで伝わったかもわからないよ。ノナちゃんの言葉……言葉とは限らないか……反応は大事だよ」
ユーリ「待ってよ! そんなポンポン言わないでよ。いま思い出してるんだから」
僕「ごめんごめん」
僕はあわてて謝った。
そうか。ユーリとノナは中学校で数学トークをするんだな。
仲良しの二人。ユーリはいろんな数学の話を知っているから、ノナに教えたいんだ。 いっしょにおしゃべりするのは楽しいからなあ……
ユーリ「……どうして、って言ってた」
僕「理由を聞いてたってこと?」
ユーリ「うん、そーだった。あのね、どうしてそれがコサインなのかって」
僕「$x$ 座標の値が $\cos\theta$ の定義だってところが伝わらなかったのかな」
ユーリ「でも、そー言ったよ! それが定義だよ、ってちゃんと言ったもん! はっきり何回も言ったのに……」
ユーリは口をとがらせて声を上げる。
なるほど、なるほど。
確かに、自分が伝えたいことが仲良しに伝わらなかったら気分はもやもやするよなあ。
僕「図は描いたの? ノナちゃんには描いてみせた方が伝わりそうだよね。だって……」
ユーリ「もちろーん! もちろん、図も描いたよー。でも、ノナはやっぱり聞いてくるの。 『どうしてそれがコサインになるのか』と、それから『コサインって何なの』って聞いてくる。 最後に『やっぱり難しい』ってなっちゃった……」
僕「ユーリが『これは定義だ』と言っても、ノナちゃんが理由を尋ねてくるっていうことは、 定義であるとはどういうことかが伝わってないのかもしれないよ」
ユーリ「えー……ちゃんと言ったのに?」
僕「ユーリが言うってことと、ノナちゃんに伝わるってことは別のことだからね。 ユーリはもちろん知ってるし、理解している。 $\cos$ の定義を知ってるだけじゃなくて、定義というものが何かを知ってるし、理解している」
ユーリ「定義って、そー決めたってことでしょ? そう決めたんだから『どうしてそれがコサインになるのか』って聞かれても答えられないもん。 『コサインって何』って言われても、『だーかーらー! この $x$ の値が $\cos\theta$ だし、 $y$ の値が $\sin\theta$ なの!』って言い合いみたいになっちゃう……」

僕「うんうん。ノナちゃんは定義するときの話の流れを誤解しているんだよ、きっと」
ユーリ「話の流れを誤解? どゆこと?」
僕「ユーリは、単位円上にある点の $x$ 座標の値を使って $\cos\theta$ を定義したよね。つまり話の流れはこうだ」
ユーリの話の流れ(正しい)
(1)「単位円上の点の $x$ 座標の値」……これは、よくわかっているものである。既知のものである。それが何かを問わなくてもいいものである。
(2)「$\cos\theta$」……これは、定義するまでわかっていないものである。未知のものである。定義して初めて定まるものである。
↓
(1)を使って、(2)を定義する。
ユーリ「めちゃめちゃくどーい! そりゃそーだよー。だって 『単位円上の点を使って、 $\cos\theta$ を定義する』ってそーゆーことじゃん!」
僕「でも、恐らくノナちゃんはそう考えてはいないと思うよ。 コサインの理由を聞いてきたり、コサインとは何かって繰り返し聞くとしたら…… 想像だけど、ノナちゃんの考えはこうなんじゃないかな」
想像したノナちゃんの考え(誤り)
(1)「単位円上の点の $x$ 座標の値」……これは、よくわかっているものである。既知のものである。それが何かを問わなくてもいいものである。
(2)「$\cos\theta$」……これも、よくわかっているはずのものである。既知のはずのものである。みんなが知っているけれど自分は知らないものである。難しそうなものである。
↓
(1)と(2)は等しいという性質がある。
ユーリ「えー……」
僕「もしもノナちゃんがこう考えていたら、ユーリの説明じゃ納得しないよね。 「単位円上の点の $x$ 座標の値」はわかるけど、 「$\cos\theta$」って何だろう……という疑問は解消しないから」
ユーリ「えー……そっかなー。定義のこともちゃんと説明したんだけどなー……」
僕「ユーリがちゃんと説明してないとは僕も思わないよ。 でも、さっきも言ったけどユーリが説明することと、ノナちゃんが理解することは別だから」
ユーリ「だって、だって、二等辺三角形の定義とか、ノナわかってたじゃん?(第305回参照)」
僕「ああ、そうだね。でも、ほら、 $\cos\theta$ っていかにも難しそうに見える。 だから『もしかしてこの $\cos\theta$ というものは、みんなが知っているけど自分だけ知らないものだ』と思い込んでしまうかも。 そうしたら、いま、まさに、それを目の前で定義しているのだ、という事実に気がつかないかもね」
ユーリ「ふーん……こんなに簡単なことなのに?」
僕「そうだね。 $\cos\theta$ は、点の $x$ 座標のことだから、すごく簡単だ。 だからかえって混乱するかも。 $\cos\theta$ という数式は、慣れていないとすごく難しそうに見える。 だから、そんなに簡単な概念のはずはない!って思い込んでしまう可能性はあるよ」
ユーリ「そーゆーもんかにゃあ……。うん、でも、今度ノナに会ったらいまの話、してみる!」
僕「ところで……木の高さを求める問題で $\tan$ を使うって、中学校の数学で出てきたっけ?」
ユーリ「んにゃ、出てこないよん。こういう問題があったの」
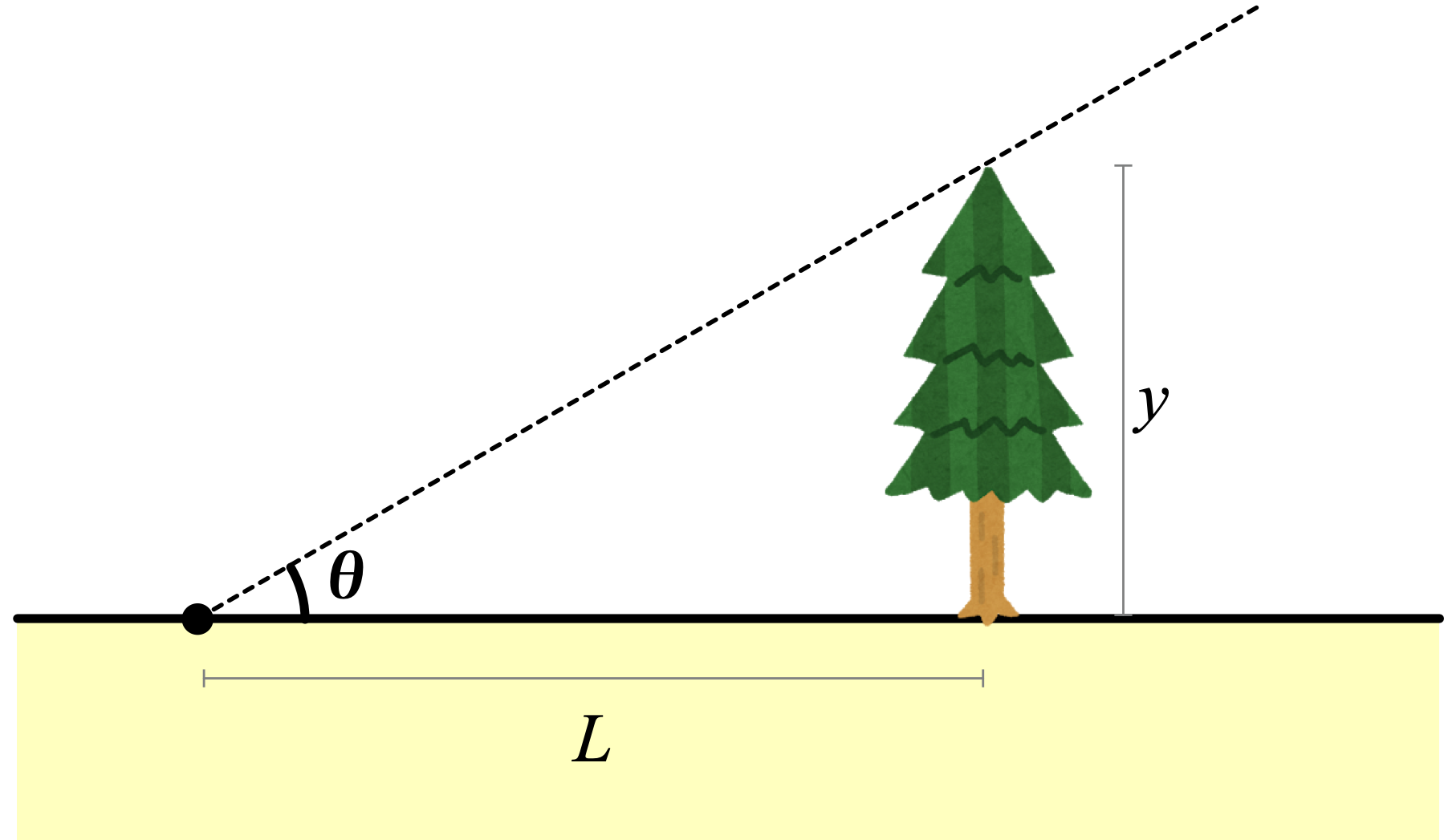
問題1
木から約17メートル離れた地点から木を見上げたとき、もっとも高いところを見上げる角度は約30度でした。
このとき、木のおよその高さを求めてください。
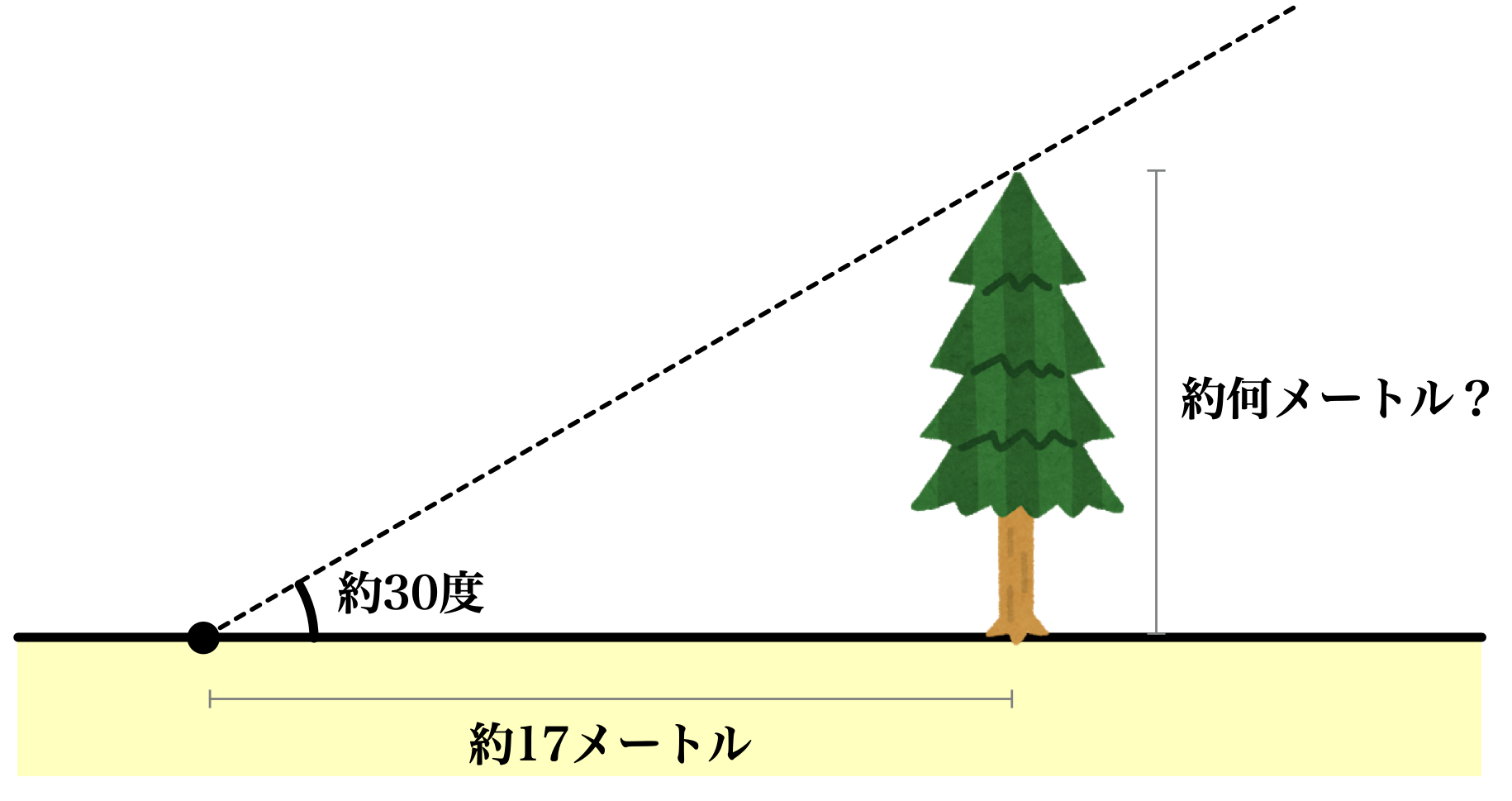
※木のイラストは「いらすとや」さんから
僕「なるほど。仰角が約30度なんだね」
ユーリ「ぎょうかく?」
僕「ある地点を見上げる角度のこと。仰ぎ見る角度(あおぎみるかくど)だから仰角」
ユーリ「へー……」
僕「ユーリはこの問題を見て『地面に顔をこすりつけるようにして木を見上げるってたいへんだにゃあ』って言ったんだろ?」
ユーリ「やだなー、そんなことゆーわけないじゃん……なぜ知ってる」
僕「ふつうは、見る人の身長を考慮した問題にするよね。それで?」
ユーリ「底辺が17センチで、一つの角度を30度にした直角三角形を描いたの。 そしたら高さが10センチになった。だから、木の高さは約10メートル」
解答1
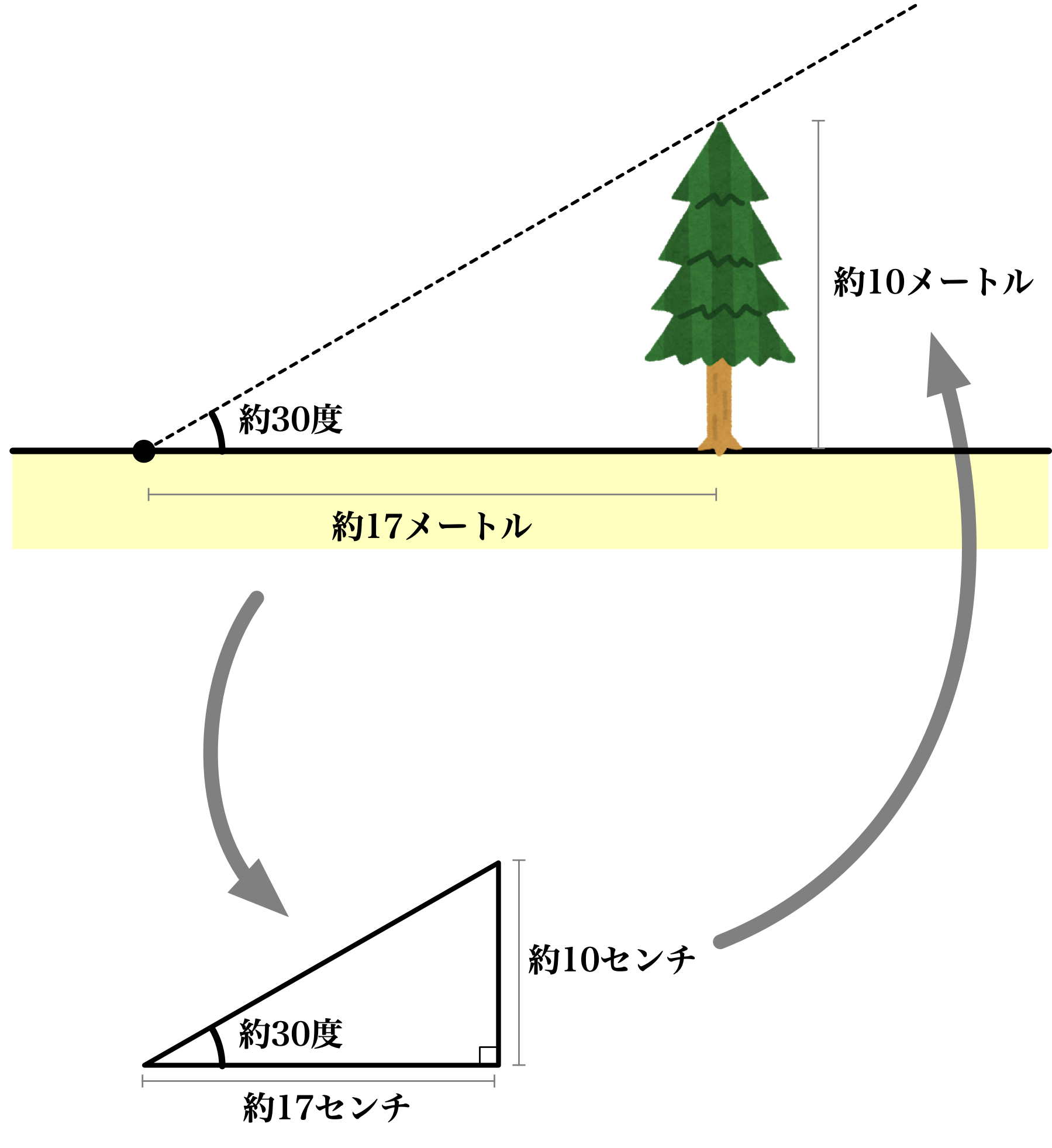
僕「なるほど! メートルをセンチに直して、直角三角形を描いて解いたんだね。三角形の相似(そうじ)だ。いいねえ!」
ユーリ「そこからもっと考えたよ。 もしも、約30度じゃなくて、正確に30度だとしたらどーなるか」
僕「お?」
ユーリ「直角三角形だから、一つの角は直角で90度になる。 一つの角が30度だから、残りの角は60度でしょ? だって、三角形の内角の和は180度だから。 つまり、正三角形を半分にした三角形ってことじゃん?」
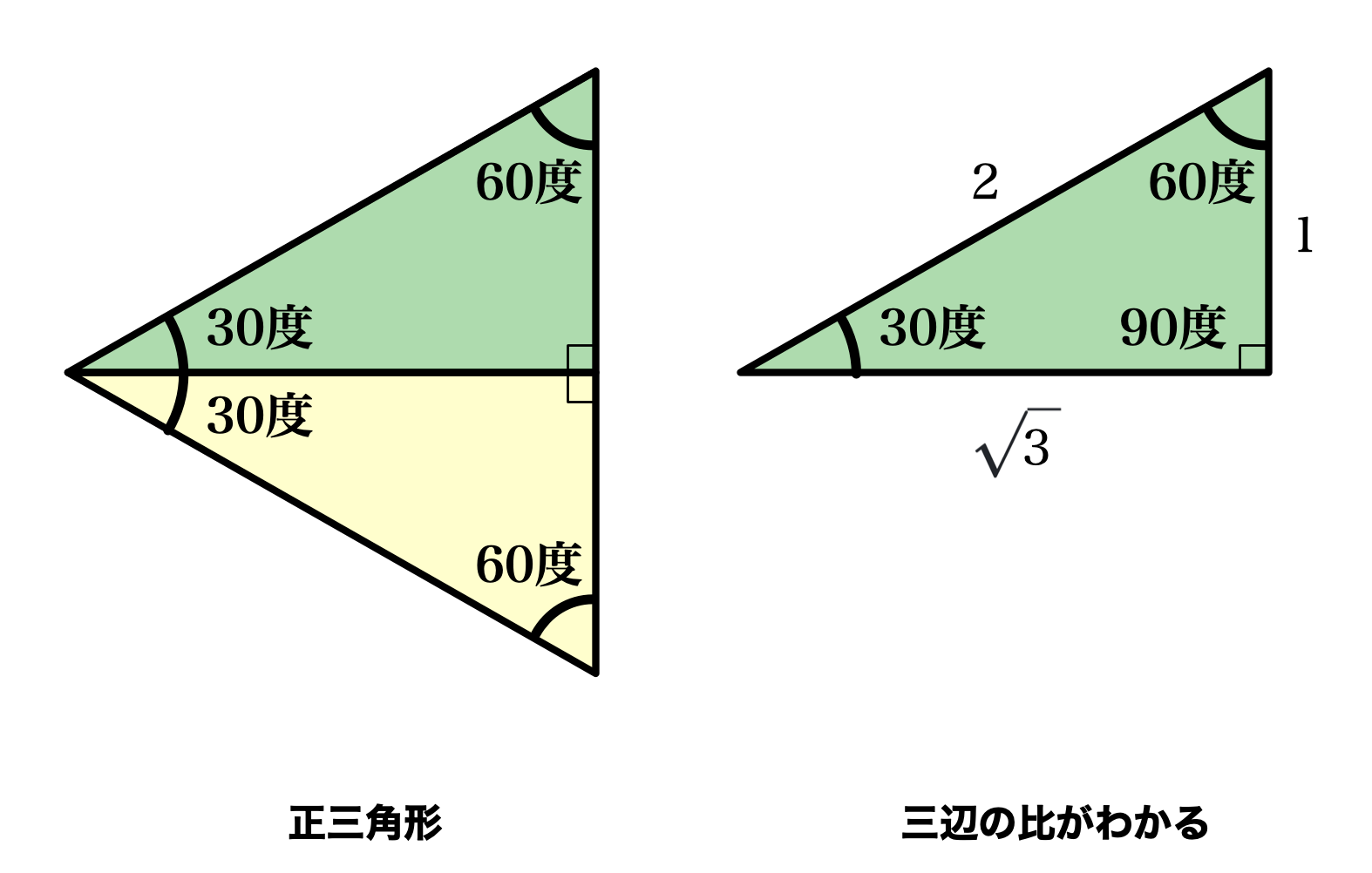
僕「いいねえ!」
ユーリ「正三角形を半分にした三角形の三辺の比は、 $1:2:\sqrt3$ になる」
僕「ユーリ、覚えてるんだ」
ユーリ「だって、よく出てくるもん」
僕「そうだね。三平方の定理でも求められる。高さを $H$ とすると……」
正三角形を二等分した直角三角形の三辺の比
高さを $H$ とする。
斜辺(直角に向かい合っている辺)の長さは高さの二倍で $2H$ になる。
三平方の定理から、 $$ \REMTEXT{底辺}^2 + \REMTEXT{高さ}^2 = \REMTEXT{斜辺}^2 $$ なので、 $$ \REMTEXT{底辺}^2 + H^2 = (2H)^2 $$ から、 $$ \REMTEXT{底辺}^2 = 3H^2 $$ となる。$\REMTEXT{底辺} > 0$だから、 $$ \REMTEXT{底辺} = \sqrt3\,H $$ になる。したがって、三辺の比は、 $$ \begin{align*} \REMTEXT{高さ}:\REMTEXT{斜辺}:\REMTEXT{底辺} &= H:2H:\sqrt3\,H \\ &= 1:2:\sqrt3 \end{align*} $$ となる。
ユーリ「そーゆーこと。ここまではノナと楽しく話をしてたんだよ。でもユーリはここでお兄ちゃんの真似しちゃった」
僕「真似? 真似って何だ?」
ユーリ「もちろん……」
僕「もちろん……?」
ユーリ「《文字の導入による一般化》でしょー!」
僕「おお!」
ユーリ「さっきの数字をぜんぶ文字にしちゃうと、一般化できるよね?」
↓《文字の導入による一般化》
僕「その通りだね。ユーリ、やるなあ。そこでノナちゃんに三角関数の話をすることになったんだね」
ユーリ「そだよん。 こーゆーふーに角度と長さを考えるときは三角関数を使うって話。 そこから図を描いて、 $\cos, \sin$ の定義の話をしたの」
$\cos$ と $\sin$
座標平面上、原点 $O$ を中心として半径 $1$ の円を描く。
円周上の点を $P$ として、図のように線分 $OP$ と $x$ 軸とのなす角を $\theta$ とする。

僕「$\tan$ の定義は?」
ユーリ「$\tan$ の定義は、 $$ \tan\theta = \frac{\sin\theta}{\cos\theta} $$ でしょ?」
$\tan$
$\cos\theta \NEQ 0$ のとき、 $$ \tan\theta = \frac{\sin\theta}{\cos\theta} $$ と定義する。
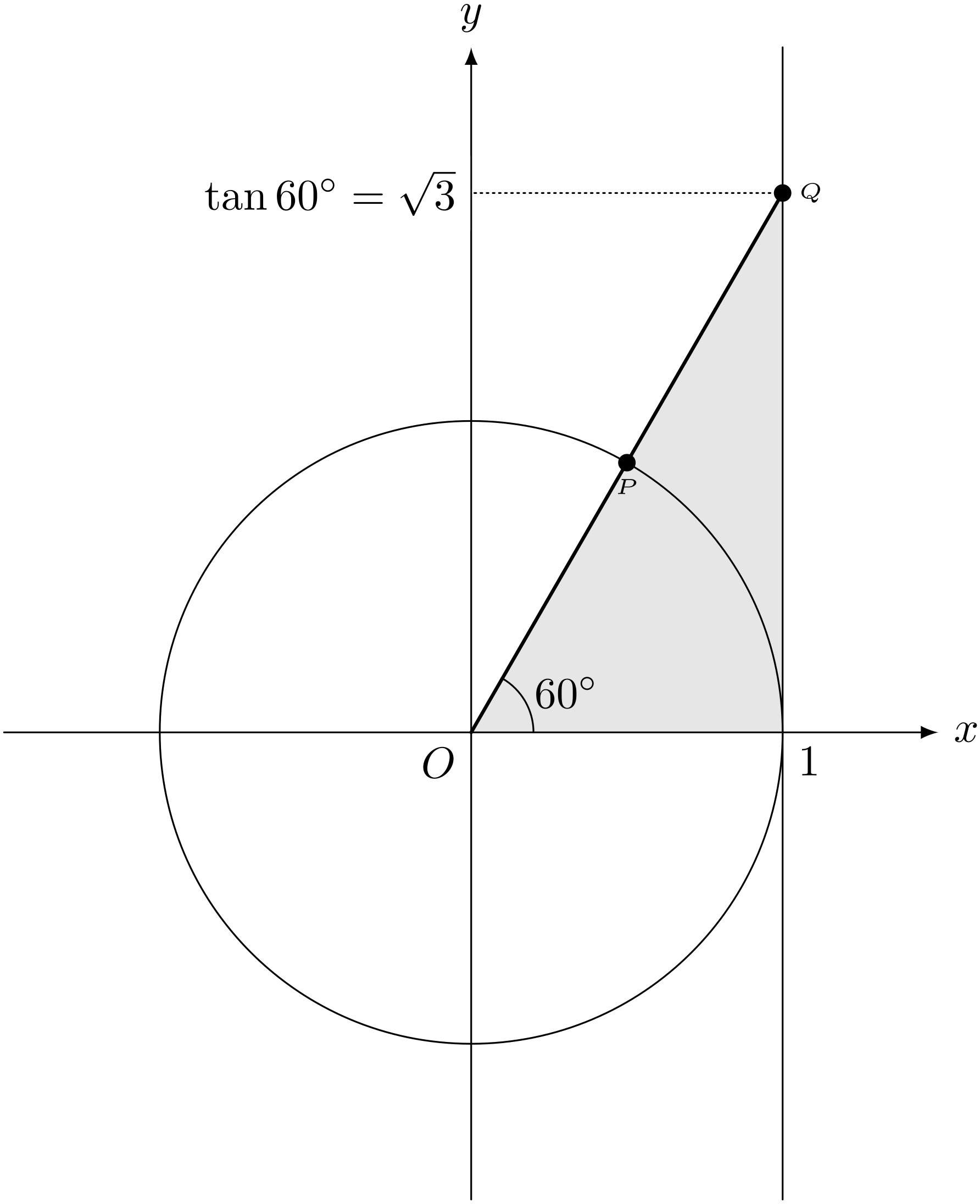
僕「そうだね。だから、ユーリの図だと、ここが $\tan\theta$ になるわけだ」
$\tan\theta$
ユーリ「えっ、そーなるの?」
僕「そうなるよ。半直線 $OP$ を描いて、 垂直な直線 $x = 1$ との交点 $Q$ を考えると、点 $Q$ の $y$ 座標が $\tan\theta$ になる。 なぜならその座標は、 $$ \frac{\sin\theta}{\cos\theta} $$ に等しくなるからね」
ユーリ「えーと……なんでだ?」
僕「木の高さを求めたときと同じだよ。この図に出てくる相似な二つの三角形を考えればわかる」
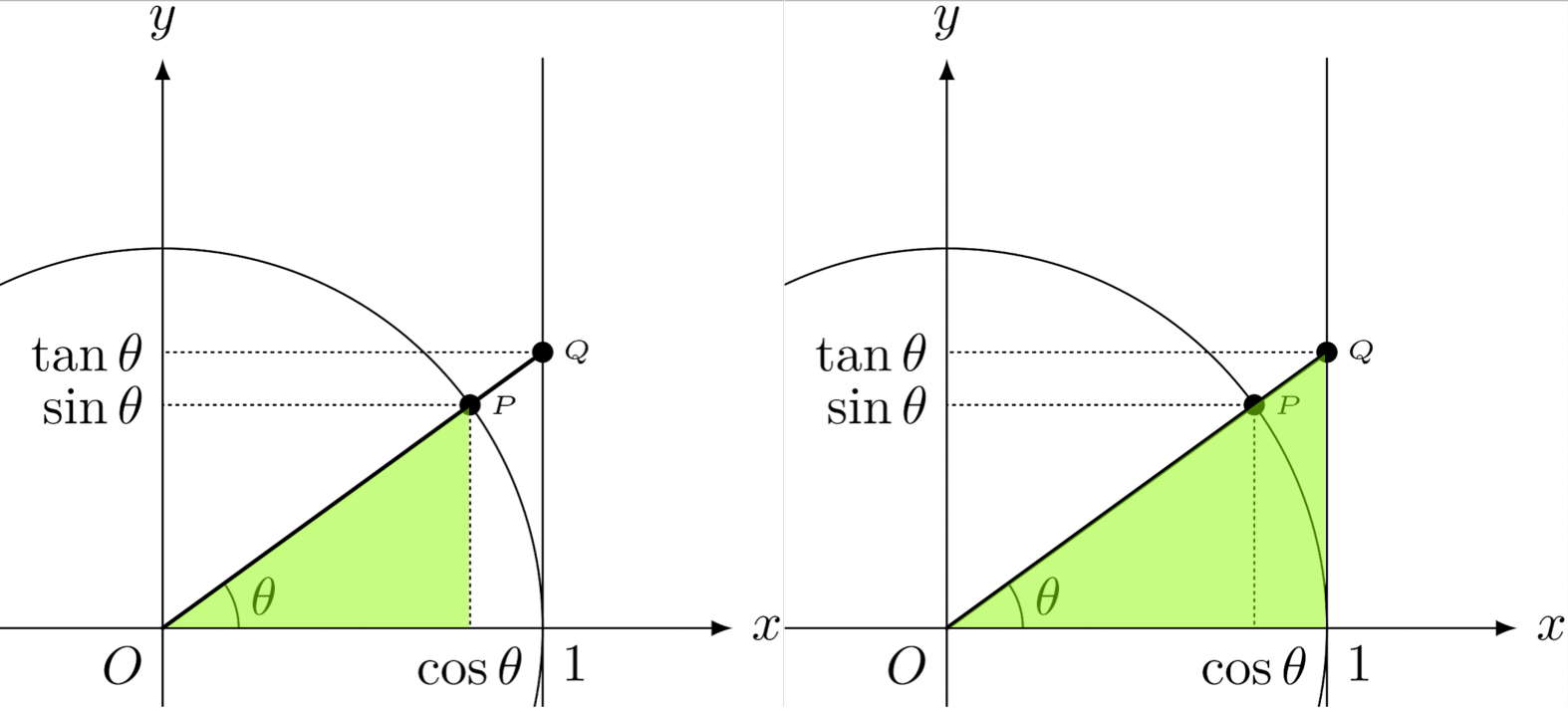
ユーリ「……」
僕「左の三角形と、右の三角形は相似だから、辺の長さの比が等しくなる。 $\frac{\REMTEXT{高さ}}{\REMTEXT{底辺}}$を考えると、左の三角形では、 $$ \frac{\REMTEXT{高さ}}{\REMTEXT{底辺}} = \frac{\sin\theta}{\cos\theta} $$ になる。右の三角形では、 $$ \frac{\REMTEXT{高さ}}{\REMTEXT{底辺}} = \frac{\REMTEXT{点$Q$の$y$座標}}{1} $$ になる。この両者が等しいんだから、 $$ \frac{\REMTEXT{点$Q$の$y$座標}}{1} = \frac{\sin\theta}{\cos\theta} $$ となり、 $$ \REMTEXT{点$Q$の$y$座標} = \tan\theta $$ がいえた」
ユーリ「あーそっかそっか。ユーリ、理解した!」
僕「もちろん、もっと簡単に考えることもできる。 左の三角形を引き延ばして右の三角形にするためには、 底辺の長さを $\cos\theta$ で割ればいい。 相似だから高さも $\cos\theta$ で割ることになる。 そこで、 $\sin\theta$ を $\cos\theta$ で割った値が、右の三角形の高さになる。 $\sin\theta$ を $\cos\theta$ で割った値って $\tan\theta$ だよね」
ユーリ「ふむふむっ!」
僕「$\tan\theta$ は、 $\cos\theta$ 分の $\sin\theta$ だから、要するに直線 $OP$ の傾きになるんだよね」
ユーリ「直線の傾き」
僕「そうだよ。『右に $\cos\theta$ だけ進めば、上に $\sin\theta$ だけ進む』としたら、 『右に $1$ だけ進めば、上にどれだけ進む?』の答えが $\tan\theta$ になる。 それは直線の傾きを表している。だから、直線$OP$のどこに三角形を作っても$\frac{\REMTEXT{高さ}}{\REMTEXT{底辺}}$の値はいつでも$\tan\theta$になる」
ユーリ「ほーほー」
僕「『右に $\cos\theta$ 進んで、上に $\sin\theta$ 進む』という傾きは $\frac{\sin\theta}{\cos\theta}$ で、これを $\tan\theta$ と定義した」
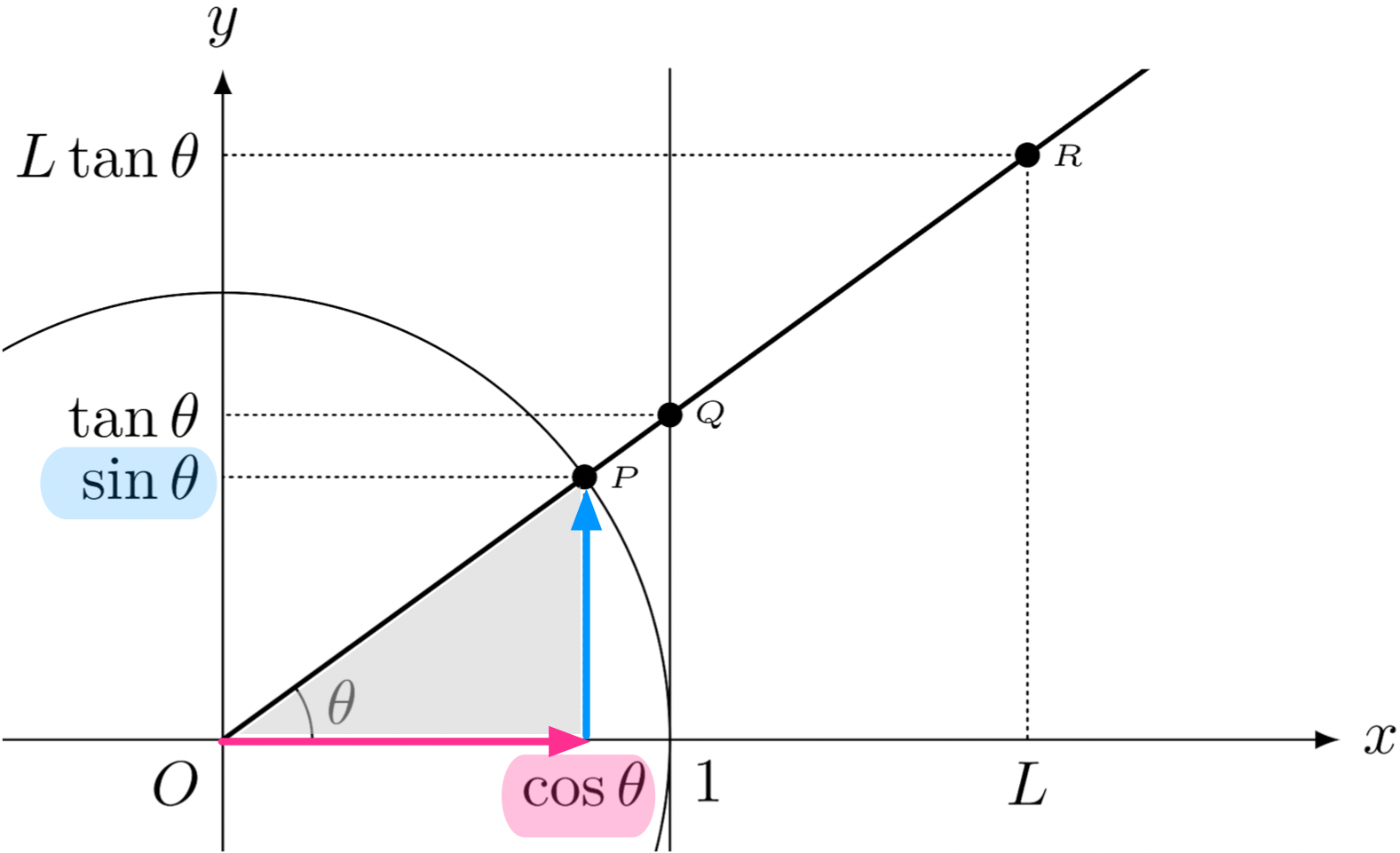
ユーリ「なーるほど。その傾きは『右に $1$ 進んで、上に $\tan\theta$ 進む』という傾きと同じってこと?」
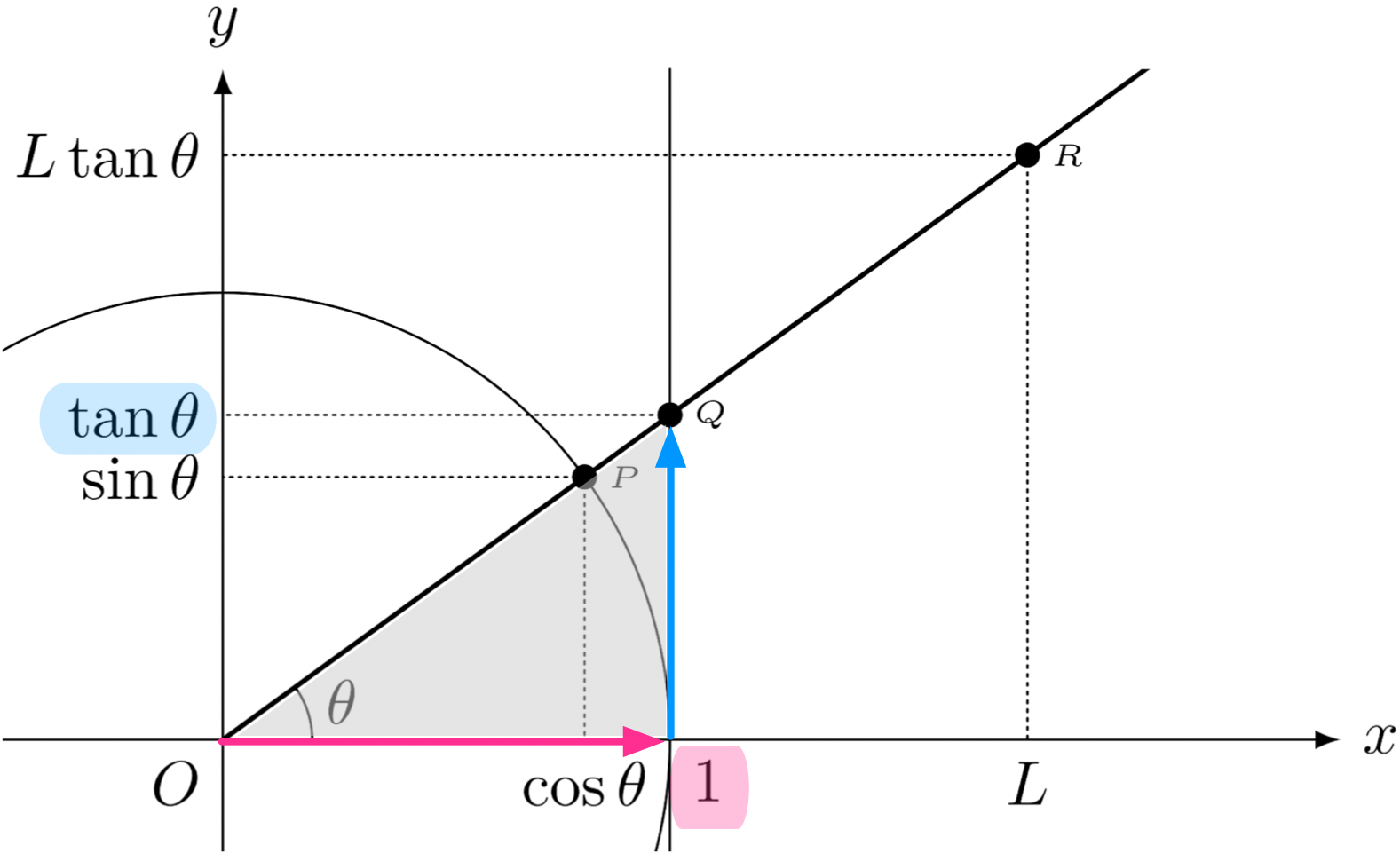
僕「そういうことだね。そしてさらに、その傾きは『右に $L$ 進んで、上に $L \tan\theta$ 進む』という傾きに等しい。 これを使って、遠いところにある木の高さを求めるわけだね」
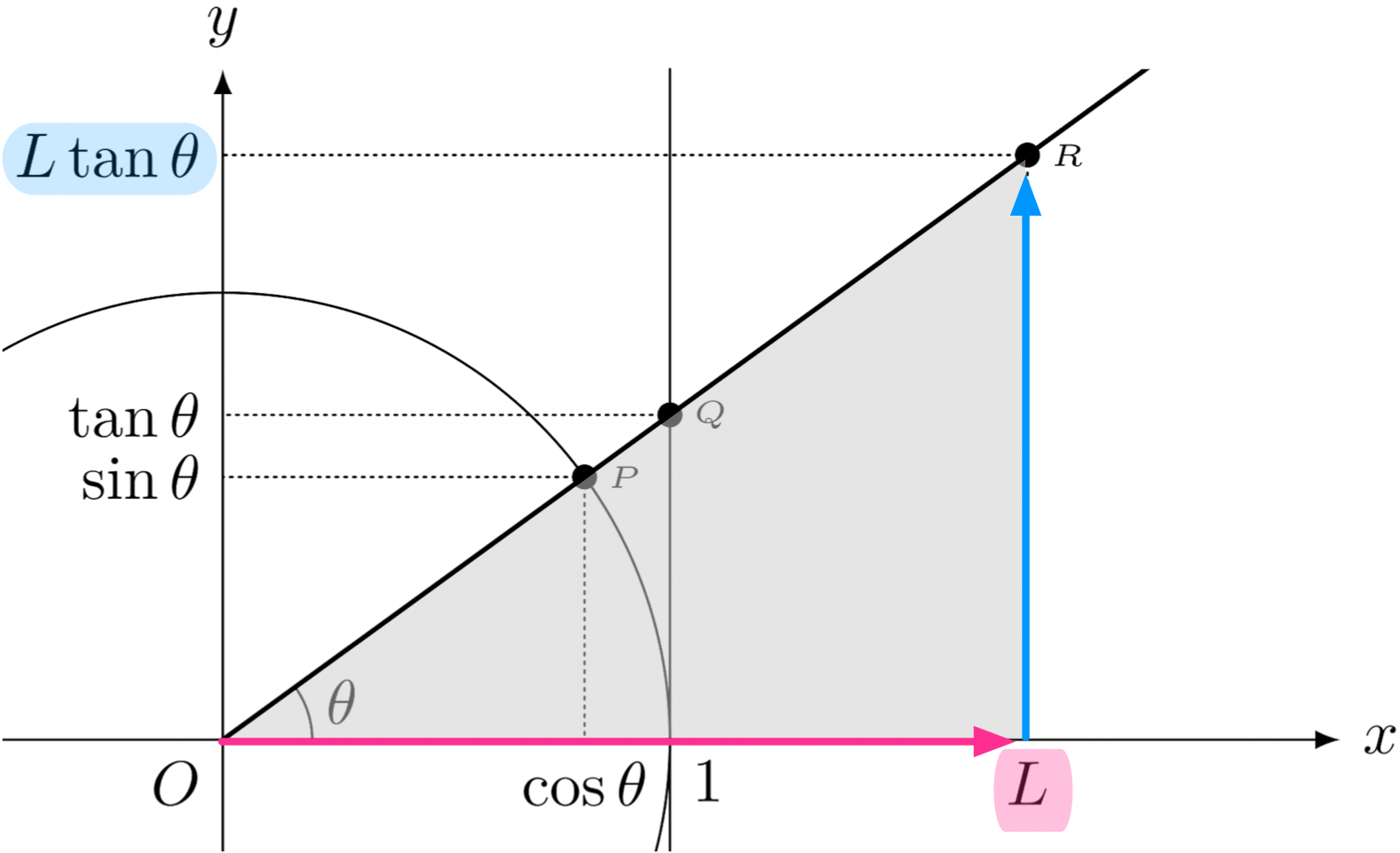
ユーリ「すげー……これで、ユーリの三角関数はカンペキだね!」
僕「そりゃすごいな。じゃあ、三角関数カンペキなユーリにクイズを出そう」
ユーリ「どんとこい」
僕「クイズ1はこれ」
クイズ1
$$ \tan\KAKUDO{45} = \REMTEXT{?} $$

ユーリ「カンタン! 答えは $1$ でしょ?」
僕「はい、正解です。どうやって求めたの?」
クイズ1の答え
$$ \tan\KAKUDO{45} = 1 $$
ユーリ「んー、一つの角が45度の直角三角形って、直角二等辺三角形だから、点 $Q$ の $y$ 座標は $1$」
$\tan\KAKUDO{45} = 1$
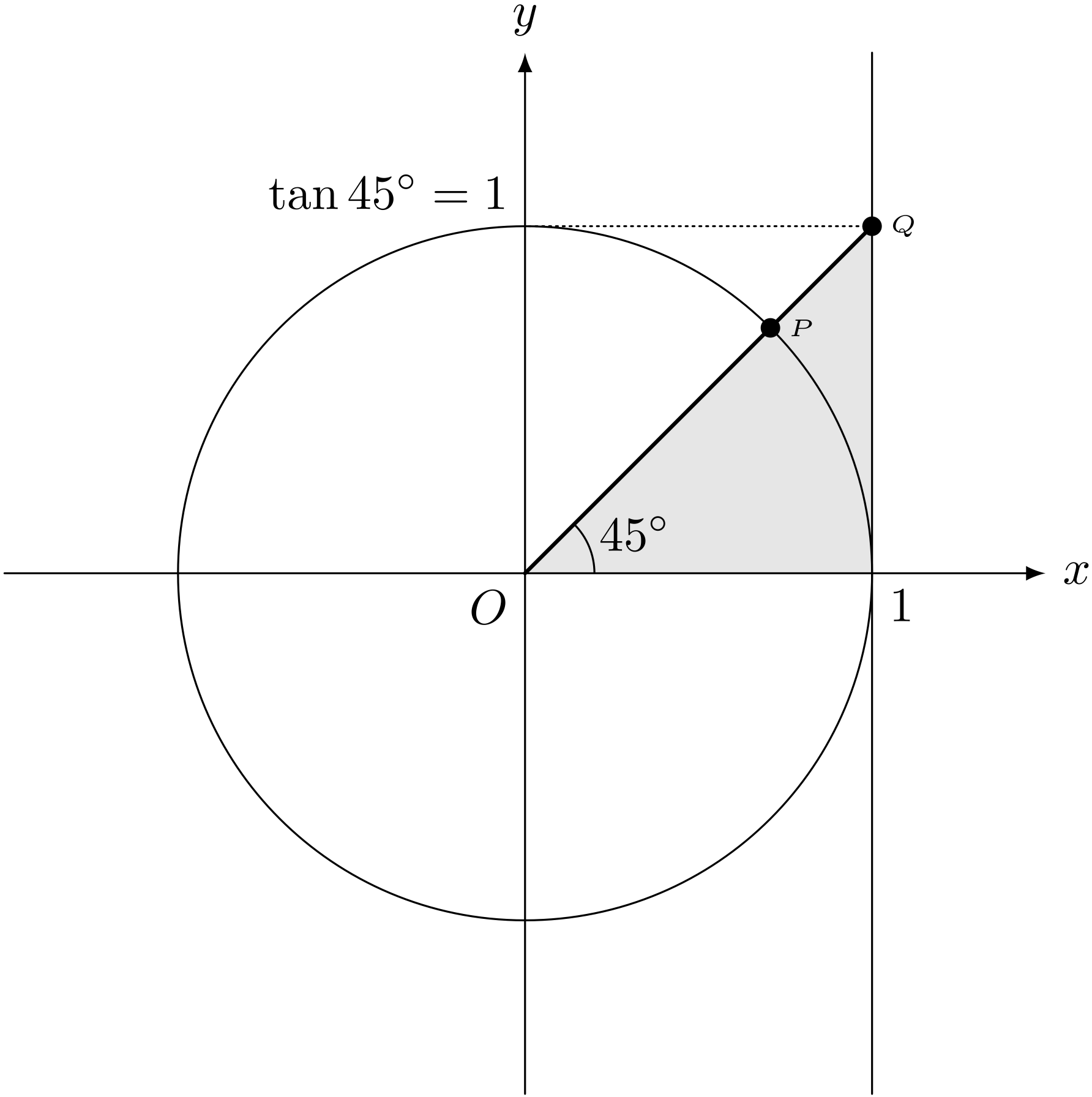
僕「そうだね、それでいいよ。もちろん、 $$ \begin{align*} \cos\KAKUDO{45} &= \frac{1}{\sqrt2} \\ \sin\KAKUDO{45} &= \frac{1}{\sqrt2} \\ \end{align*} $$ から、 $$ \begin{align*} \tan{\KAKUDO{45}} &= \frac{\sin{\KAKUDO{45}}}{\cos{\KAKUDO{45}}} \\ &= \frac{\frac{1}{\sqrt2}}{\frac{1}{\sqrt2}} \\ &= 1 \end{align*} $$ としても同じ」
ユーリ「ふんふん」
僕「じゃあ、クイズ2だよ」
クイズ2
$$ \tan\KAKUDO{30} = \REMTEXT{?} $$

ユーリ「これはさっきやったじゃん。答えは $\sqrt3$ ……じゃない! えーと、底辺が $1$ だから、 $1:2:\sqrt3$ を考えると、高さは $1$ を $\sqrt3$ で割ればいい! だから、答えは $\frac{1}{\sqrt3}$ じゃね?」
$\tan\KAKUDO{30} = \frac{1}{\sqrt{3}}$
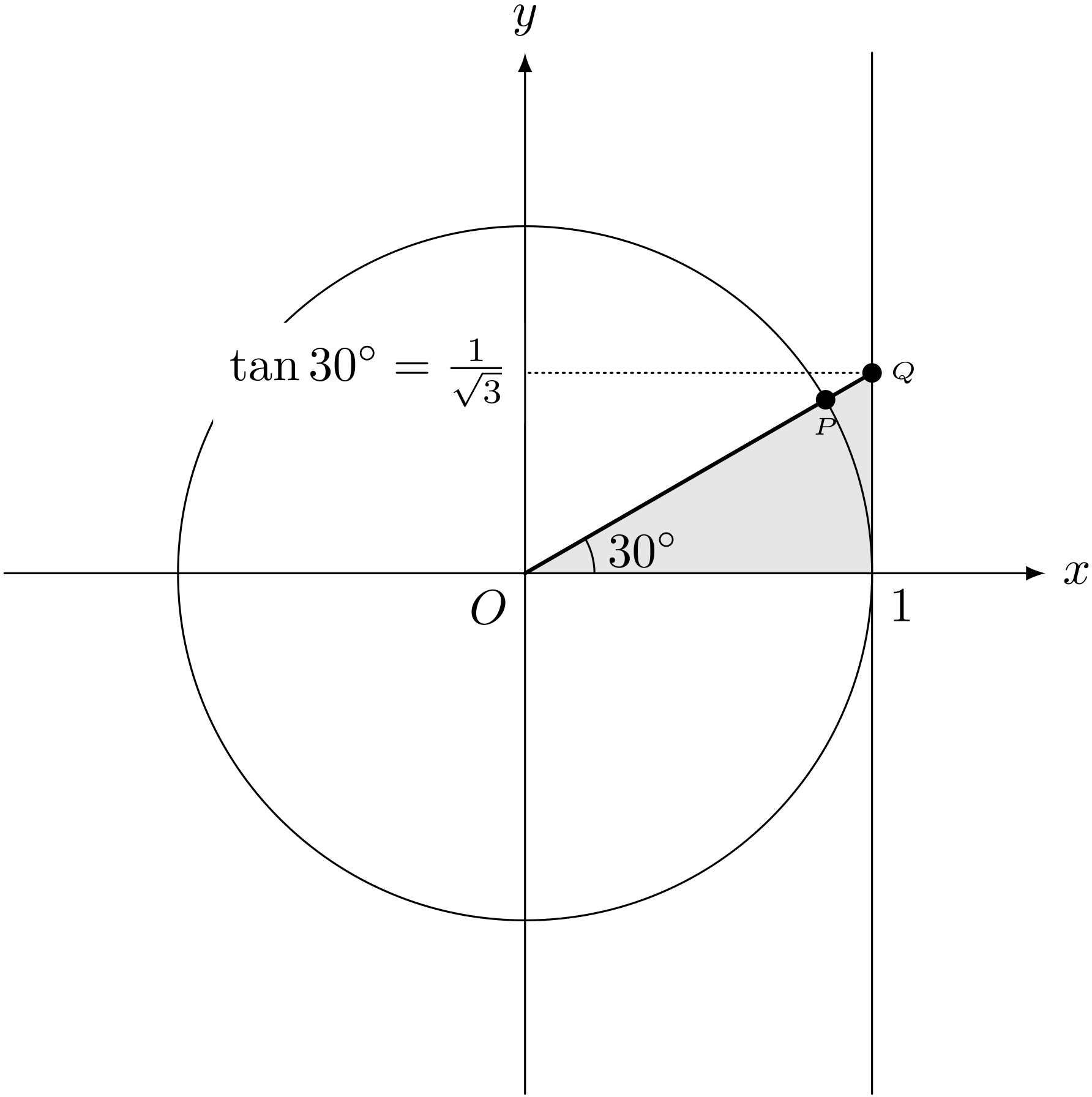
僕「うん、それでいいね。ところで、 $\frac{1}{\sqrt3}$ ってどのくらいの大きさか、わかる?」
ユーリ「だいたい $1 \div 1.7$ くらいだから、えーと、 $1$ よりは小さい?」
僕「$\tan\KAKUDO{45} = 1$ だから、 $1$ より小さいのは確かだね。 暗算で $1 \div 1.7$ は厳しいけど、有理化して $\frac{\sqrt3}{3}$ にすれば、 $1.7 \div 3$ になって、 $0.6$ より少し小さいというのがわかる」
$$ \begin{align*} \frac{1}{\sqrt3} &= \frac{1 \times \sqrt3}{\sqrt3 \times \sqrt3} && \REMTEXT{分子と分母に$\sqrt3$を掛けた} \\ &= \frac{\sqrt3}{3} && \REMTEXT{$\sqrt3 \times \sqrt3 = 3$から} \\ &= \frac{1.73\cdots}{3} && \REMTEXT{$\sqrt3 = 1.7320508\cdots$から} \\ &= 0.577\cdots \end{align*} $$ユーリ「ユーリか?」
僕「分母の有理化。 分子と分母に $\sqrt3$ を掛けると分母が $3$ になる。 分母を $3$ にすると割り算がしやすいから大きさもわかりやすい」
ユーリ「細かいテクじゃのう」
僕「じゃ、クイズ3」
クイズ3
$$ \tan\KAKUDO{60} = \REMTEXT{?} $$

ユーリ「あっ、これは $\sqrt3$ だね」
僕「はい、正解。速いな! どうやって計算したの?」
ユーリ「さっきの三角形の向きを変えればわかる。正三角形の半分になってた直角三角形を《ぱたん》ってひっくり返すの」
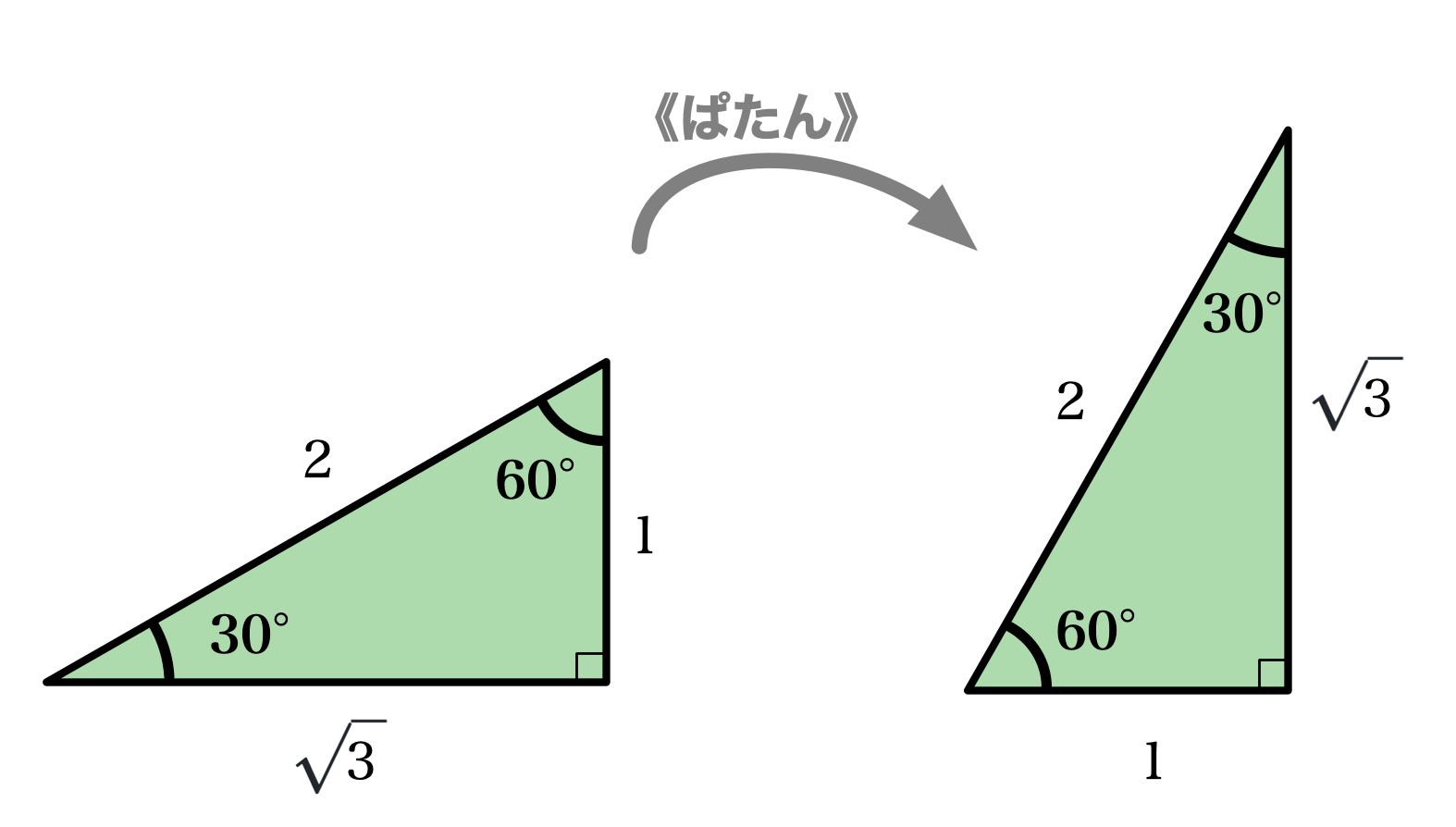
$\tan\KAKUDO{60} = \sqrt{3}$
僕「そうだね。仰角を30度にするんじゃなくて、60度にしたわけだ」
ユーリ「カンタンすぎ!」
僕「簡単すぎる? それじゃあ、こんなクイズは?」
クイズ4
$\KAKUDO{0} < \theta < \KAKUDO{90}$ とする。
$$ \tan\theta \tan(\KAKUDO{90} - \theta) = \REMTEXT{?} $$
ユーリ「えーっ! ちょっと待ってちょっと待って。何これー?」
僕「計算問題だよ。 $\tan\theta$ と $\tan(\KAKUDO{90} - \theta)$ を掛けたら何になるか?」
ユーリ「$\tan$ の公式なんて覚えてないもん!」
僕「覚えてなくてもわかるよ。よく考えればわかる。暗算でもわかるけど、紙に描いてもいいよ」

ユーリ「うーん……」
僕「紙に描いてもいいよ」
ユーリ「わかんない。紙に何を描けばいーかもわかんない」
僕「ユーリはこのクイズ4を見て何を考えた?」
ユーリ「$\KAKUDO{90} - \theta$ って何だろってずーっと思ってる」
僕「なるほど。そうだよね。他には?」
ユーリ「他には……掛け算の結果は、 $\theta$ の式になるんだよね?」
僕「そうとは限らないよ」
ユーリ「だって、 $\theta$ は文字でしょ?」
僕「文字だね。そして $\KAKUDO{0} < \theta < \KAKUDO{90}$ の範囲の値を取ると仮定している」
ユーリ「だから、 $\theta$ はどんな数になるかわからない……ダメ。わかんない。ヒントほしーなー(ちらっちらっ)」
僕「ヒントはクイズ2とクイズ3だよ」
ユーリ「クイズ2とクイズ3?」
僕「こうだったよね」
クイズ2とクイズ3の結果 $$ \tan{\KAKUDO{30}} = \frac{1}{\sqrt3}, \qquad \tan{\KAKUDO{60}} = \sqrt3 $$
ユーリ「え、もしかして、 $\theta = \KAKUDO{30}$ で考えるってこと?」
僕「$\theta = \KAKUDO{30}$ だとしたらどうなるかな?」
ユーリ「こーなる……けど」
$\theta = \KAKUDO{30}$ のとき、 $$ \begin{align*} \tan\theta \tan(\KAKUDO{90} - \theta) &= \tan\KAKUDO{30} \tan(\KAKUDO{90} - \KAKUDO{30}) && \REMTEXT{$\theta = \KAKUDO{30}$だから} \\ &= \tan{\KAKUDO{30}} \tan{\KAKUDO{60}} && \REMTEXT{$\KAKUDO{90} - \KAKUDO{30} = \KAKUDO{60}$だから} \\ &= \frac{1}{\sqrt3} \times \sqrt3 && \REMTEXT{クイズ2とクイズ3から} \\ &= 1 \\ \end{align*} $$
僕「そうだね。 $\theta = \KAKUDO{30}$ のとき、 $$ \tan\theta \tan(\KAKUDO{90} - \theta) = 1 $$ がいえた。それで?」
ユーリ「もしかしてだけど、 $\KAKUDO{30}$ 以外のときも……いつでも…… $$ \tan\theta \tan(\KAKUDO{90} - \theta) = 1 $$ になるの?」
僕「どうだろうね。たとえばクイズ1を思い出してみると、どうかな?」
クイズ1の結果 $$ \begin{align*} \tan{\KAKUDO{45}} &= 1 \end{align*} $$
ユーリ「あっ、このときも $1$ になる!」
$\theta = \KAKUDO{45}$ のとき、 $$ \begin{align*} \tan\theta \tan(\KAKUDO{90} - \theta) &= \tan\KAKUDO{45} \tan(\KAKUDO{90} - \KAKUDO{45}) && \REMTEXT{$\theta = \KAKUDO{45}$だから} \\ &= \tan{\KAKUDO{45}} \tan{\KAKUDO{45}} && \REMTEXT{$\KAKUDO{90} - \KAKUDO{45} = \KAKUDO{45}$だから} \\ &= 1 \times 1 && \REMTEXT{クイズ1から} \\ &= 1 \\ \end{align*} $$
僕「そうだね」
ユーリ「きっと、いつでも、 $$ \tan\theta \tan(\KAKUDO{90} - \theta) = 1 $$ になるんだよ! 絶対そーだ!」
僕「うん、それは《ユーリの予想》だ。素晴らしい! でもそれは、予想に過ぎない」
ユーリ「証明するまでは、予想に過ぎない……ってか! 待って待って。証明する! もうわかったもん!」
問題2
$\KAKUDO{0} < \theta < \KAKUDO{90}$ のとき、
$$ \tan\theta \tan(\KAKUDO{90} - \theta) = 1 $$
が成り立つことを証明せよ。
ユーリはすばやく紙に図形を描いた。

僕「できたの?」
ユーリ「できたできた。クイズ3のときの《ぱたん》と同じことやればOK!」
解答2
図(左)の直角三角形ABCで、角ABCの大きさを $\theta$ とし、辺BCの長さを $1$ とすると、辺ACの長さは $\tan\theta$ になる。
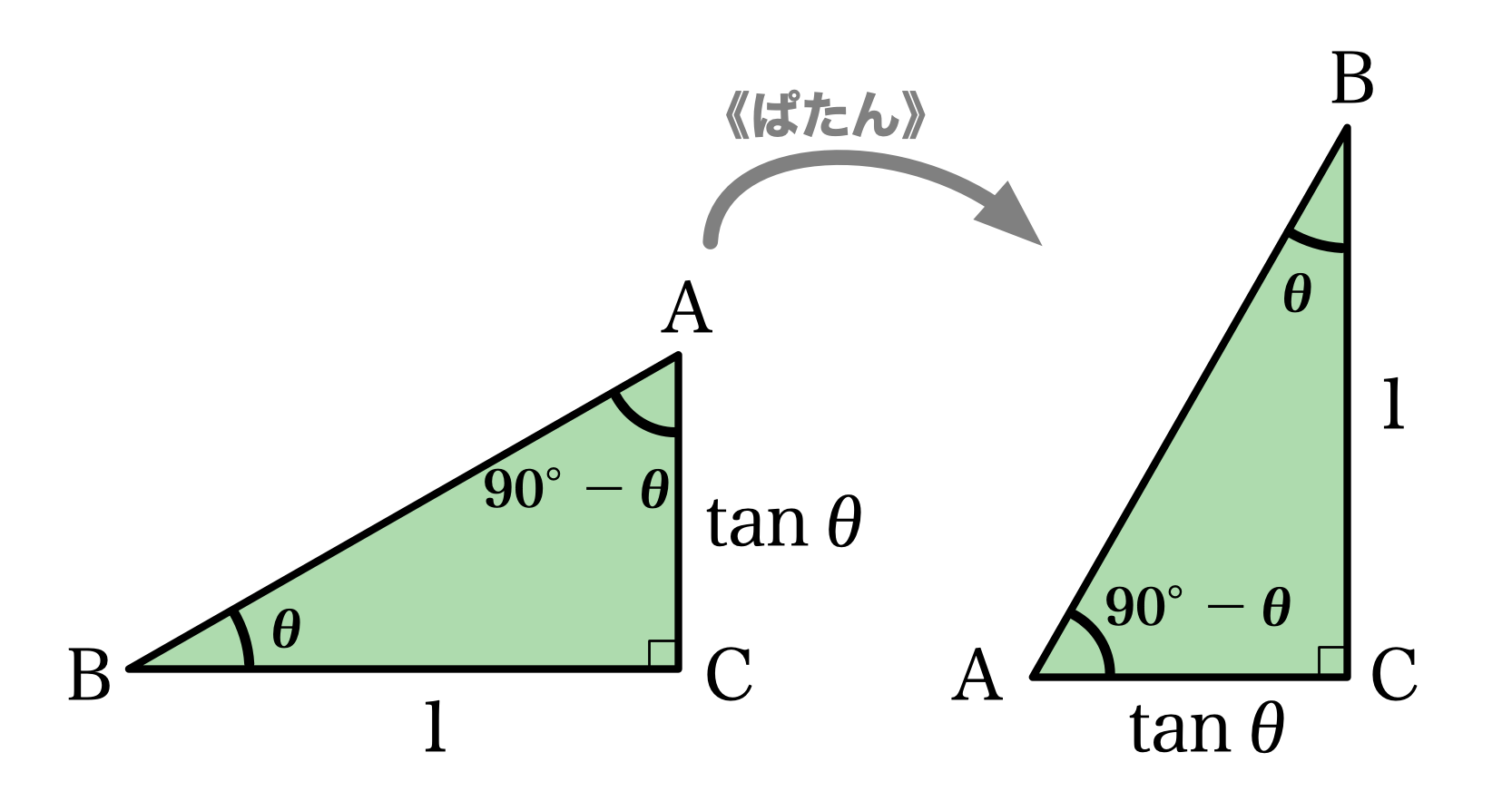
三角形の内角の和は180度なので、角BACの大きさは $\KAKUDO{90} - \theta$ となるので、 図(右)から、 $$ \tan(\KAKUDO{90} - \theta) = \frac{1}{\tan\theta} $$ である。
したがって、 $$ \tan\theta\tan(\KAKUDO{90} - \theta) = \tan\theta \cdot \frac{1}{\tan\theta} = 1 $$ となる。
(証明終わり)
僕「いいね!」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第311回終わり)
(2021年1月8日)