第290回 シーズン29 エピソード10

音楽と数学：表現と探求（後編）

双倉図書館にて

僕「……だから、《半音上げる》という操作をこのオイラー格子に当てはめられるよね」

テトラ「《半音上げる》という操作……」

僕「言葉で説明するよりも、図に書き込んだ方がいいかな。こういうことを考えていたんだ。 まず、 $C(0,0)$ を $C\sharp(-1,2)$ に動かすことを考える」

テトラ「なるほど、 $C$ を $C\sharp$ に半音上げるのを矢印で表すんですね。ベクトルのように」

僕「そう、まさにベクトルなんだ。すべての音が $(-1,2)$ のベクトルを加えると半音上がるから！」

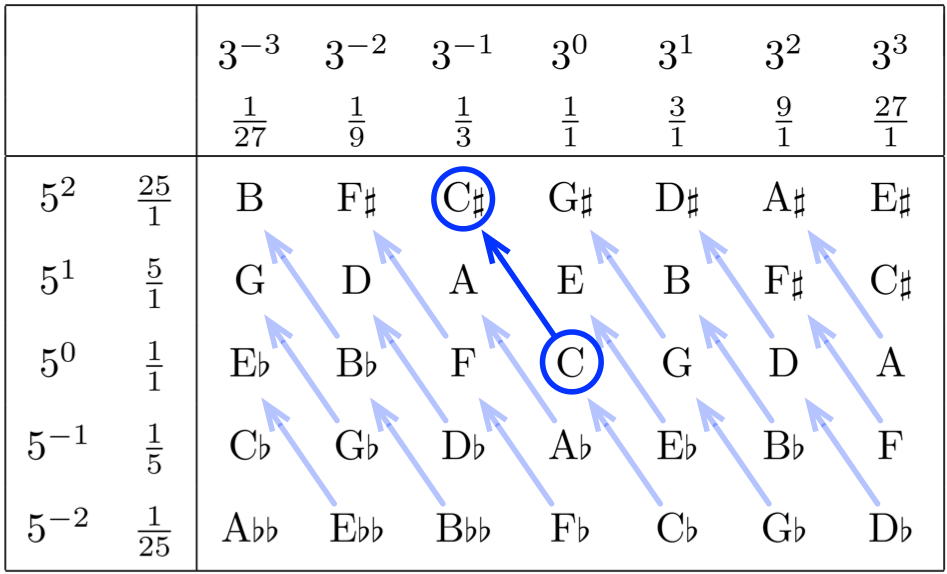
テトラ「ああ、なるほどです」

僕「そして、 $C\sharp$ は $C\sharp(-1,2)$ だけじゃなくて、 $C\sharp(3,1)$ にもあるから、 $(3,1)$ のベクトルを使うこともできる！」

ユーリ「むむむ、これってどーゆーこと？」

僕「さっきまでの話と同じだよ。 オイラー格子が表しているのは、基準とした音 $C(0,0)$ の周波数を何倍すれば特定の音が作れるかを表している」

ユーリ「うん」

テトラ「右に動くと $3$ 倍、左に動くと $1/3$ 倍。上に動くと $5$ 倍、下に動くと $1/5$ 倍……ですね」

ユーリ「で？　それで《半音上げる》のが何で二通りあるの？」

僕「それは《半音上げる》の半音という音程を、 $2^\ell3^m5^n$ 倍で近似する方法が一通りじゃないってことだよ、きっと」

ユーリ「ははーん……そっか、 $A$ という音を、 $A(-1,1)$ と $A(3,0)$ の二通りで表したのと同じってこと？」

僕「きっとそうだよ。だから、オイラー格子を座標平面に見立てたときの $(-1,2)$ と $(3,1)$ はとても近いんじゃないかな？」

ユーリ「けーさん、してみよー！」

テトラ「たとえば $(-1,2)$ というベクトルは、オイラー格子の表す意味を考えると、 $2^j3^{-1}5^2$ 倍ということですね。 $j$ を整数として……」

僕「そうだね。オクターブ内に収めるには $j$ の調整がいるけどね。 たとえば $j = 0$ とすると $2^03^{-1}5^2 = 25/3 = 8.333\cdots$ だから、 $8$ オクターブも上になってしまうから」

ユーリ「$8$ 倍って、 $8$ オクターブ上なの？」

僕「おっと、 $2$ 倍するごとに $1$ オクターブだから違った。 $1 \to 2 \to 4 \to 8$ だから、 $3$ オクターブ上だったね。 ともかく、それじゃ大きすぎるから、 $2$ で割っていって $1$ 以上 $2$ 未満になるようにしよう」

$$ \begin{align*} 2^0 \times 25/3 &= 25/3 = 8.333\cdots & (j = 0) \\ 2^{-1} \times 25/3 &= 25/6 = 4.1666\cdots & (j = -1) \\ 2^{-2} \times 25/3 &= 25/12 = 2.08333\cdots & (j = -2) \\ 2^{-3} \times 25/3 &= 25/24 = 1.041666\cdots & (j = -3) \\ \end{align*} $$

ユーリ「いまのは $(-1,2)$ だから、 $(3,1)$ も同じことするんでしょ？　 $2^k3^35^1$ で」

テトラ「そうですね……ええと」

ユーリ「ユーリがやる！　 $k = 0$ のときは、 $2^03^35^1 = 27\times 5 = 135$ だから、大きすぎ。だから、 $2$ で割ってくぞっと！」

$$ \begin{align*} 2^0 \times 27\times 5 &= 135 & (k = 0) \\ 2^{-1} \times 27\times 5 &= 135/2 = 67.5 & (k = -1) \\ 2^{-2} \times 27\times 5 &= 135/4 = 33.75 & (k = -2) \\ 2^{-3} \times 27\times 5 &= 135/8 = 16.875 & (k = -3) \\ 2^{-4} \times 27\times 5 &= 135/16 = 8.4375 & (k = -4) \\ 2^{-5} \times 27\times 5 &= 135/32 = 4.21875 & (k = -5) \\ 2^{-6} \times 27\times 5 &= 135/64 = 2.109375 & (k = -6) \\ 2^{-7} \times 27\times 5 &= 135/128 = 1.0546875 & (k = -7) \\ \end{align*} $$

僕「あ、確かに近い値になるね。 $2^j3^{-1}5^2$ で $j = -3$ にしたときと、 $2^k3^35^1$ で $k = -7$ にしたとき」

$$ \begin{align*} 2^{-3} \times 25/3 &= \UL{1.0}41666\cdots & (j = -3) \\ 2^{-7} \times 27\times 5 &= \UL{1.0}546875 & (k = -7) \\ \end{align*} $$

ユーリ「そっか……どうやっても、バシッと同じ値にはならないんだ」

僕「そうそう。 $2^j3^{-1}5^2 = 2^k3^35^1$ を満たすような整数の組 $j,k$ は存在しないから」

ユーリ「うまーく音を散らばせるれらて……散らばすられるればいい？」

僕「うん、そう。うまく音を散らばせられればいいんだけど、そうはいかない。 オイラー格子ではあくまで $3$ と $5$ という整数倍を生かそうとしているからね。 純正律の響きを作りつつ進むなら、半音にもいろんな可能性が出て来てしまう」

テトラ「うまく音を散らしたものが平均律ともいえますね。 オクターブ以外の整数倍をすべてにおいてあきらめる代わりに、 どの音も同じ扱いにするわけですから（第285回参照）」

ユーリ「そっか……」

音程

僕「オクターブは $2$ 倍で完全八度。それはシンプルでいいんだけど、その途中をどう割るかだね。 ピタゴラス音律でも、純正律でも最初は同じ。 $C$ から $G$ を作るものだった。つまり完全五度の音程を作る」

ユーリ「えーと、完全五度って $3/2$ 倍だよね……」

テトラ「そうですね。周波数だと $3/2$ 倍で、楽譜だとこうです」

ユーリ「完全五度の楽譜……あのね、楽譜よりピアノみたいな図の方がいーかにゃあ……」

僕「ユーリは何か考えてるの？」

ユーリ「純正律のとこで完全五度とか、長三度とか出てきたじゃん？　あれって、そもそも半音何個分なのかって考えてた（第287回参照）」

僕「ああ、なるほど」

ユーリ「音程の呼び方ってめんどくさいんだもん。音の高さが同じだったら完全ゼロ度にすればいいのに完全一度だったし」

テトラ「そういえばそうですね」

僕「歴史的な事情があるのかな……」

ユーリ「だからね、音程を半音何個分に直したらどーなんのかなって思ったのさ！」

僕「それはいいね！　自分の理解のために自分で整理し直す態度だ。それはね」

ユーリ「《先生トーク》はさておき、早く図を描こうよ！」

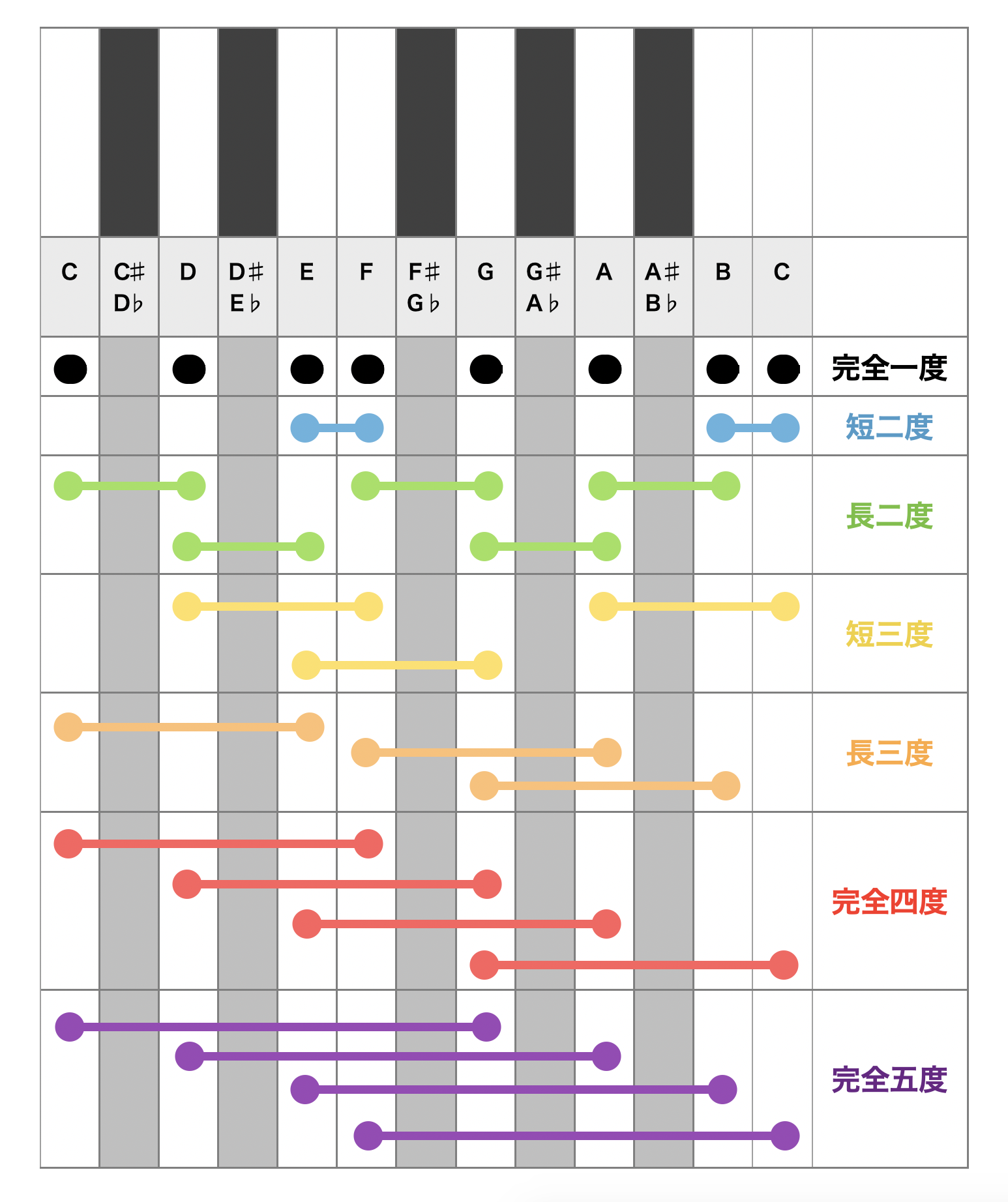
ユーリ「だいぶすっきりした……かにゃ？」

テトラ「そうですね」

• 半音0個分：完全一度
• 半音1個分：短二度
• 半音2個分：長二度
• 半音3個分：短三度
• 半音4個分：長三度
• 半音5個分：完全四度
• 半音7個分：完全五度

ユーリ「……」

僕「今度は何を考えているんだろう。ねえ、ユーリ？」

ユーリ「なんでごちゃごちゃするのかを考えてたの」

僕「へえ」

ユーリ「名前が決まってないからかなーって？」

僕「名前が決まってない？」

ユーリ「んにゃ、名前は決まってんだけど、音が決まってないから」

僕「音が決まってない……？」

ユーリ「あーもー、毎回聞き返さないで、わかれよー！」

僕「だって、ユーリが何を考えているかは、言葉にしてもらわなくちゃわからないじゃないか」

ユーリ「言葉にできるくらいなら、もーしてるよー！　言葉にできないからわかれって言ってんじゃん！」

僕「そうだけど……」

テトラ「先輩、ちょっとお待ちください。 ユーリちゃんはさっきも $A$ という名前が二箇所あることを気にしていましたよね。 もしかしてですが、《一つの名前が一つのものを表していない》ことに引っかかるのではありませんか？」

ユーリ「それ！それ！　さっすがテトラさん」