第285回 シーズン29 エピソード5

音楽と数学：自由な平均律（前編）

双倉図書館にて

ユーリ「……なーるほど。ユーリが見つけたパターンだとこーなるね！」

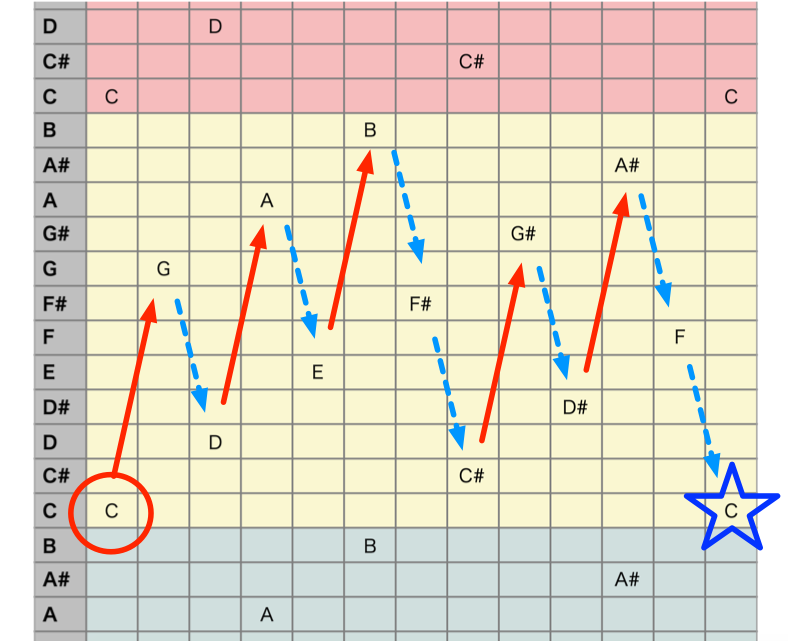
僕「そうなる。そして問題は左下と右下の音 $C$ だよ。 左下の赤い丸で囲んだのが最初の音 $C$ で、右下の青い星で囲んだのが十三音目の音 $C$ だ」

テトラ「その二つの音の周波数が等しくないということなんですね……」

ユーリ「うわー……」

テトラ「こちらにピタゴラスコンマの解説パネルがあります」

ユーリ「ぴたごらすこんま！　名前があるんだ！」

僕「そうか、ここでいう《違い》は周波数の比になるわけか」

ユーリ「え？」

僕「日本語で《違い》というと、差を意味することもある。でもここでは比の意味」

ユーリ「よくわかんない」

僕「難しい話を言ってるわけじゃないよ。 《最初の音の周波数》を $C_1$ で表して、《十三音目の周波数》をたとえば $C_{13}$ で表したとする。 ピタゴラスコンマは $3^{12}/2^{19}$ だから、 $$ C_1 \times \underbrace{\dfrac{3^{12}}{2^{19}}}_{\REMTEXT{ピタゴラスコンマ}} = C_{13} $$ になるって言っただけ。もしもピタゴラスコンマが $1$ だったら《違い》はまったくなかったんだけどね。 $C_1 \times 1 = C_{13}$ になってたわけだから。 でも、実際はピタゴラスコンマは、 $$ 1.013643{}26477{}05078125 $$ という値。 $1$ よりもちょっぴり大きい」

ユーリ「比の意味、わかった。 いままでずっと周波数を $3$ 倍したり $1/2$ にしてきたんだから、ぜーんぶ掛け算の話だもん。 それにしても、この《小さい違い》はどーすんの？」

テトラ「……それでいいんでしょうか」

ユーリ「テトラさん、それって？」

テトラ「あたしたちは計算の方法を知りましたよね」

ユーリ「？」

テトラ「計算の方法を知ったということは《小さい》ではなくて《どのくらい小さい》と言えるようになったはずだと思うんです。 なので、ピタゴラスコンマはどのくらい小さいのかな……と」

ユーリ「あっ！　定量的な議論ってやつ？！　（第282回参照）」

僕「なるほど……」

ユーリ「でも待ってよ、テトラさん。だって、もー、計算は終わってるじゃん？ ピタゴラスコンマは、 $$ 3^{12}/2^{19} = 531441 / 524288 = 1.013643{}264770{}5078125 $$ だってわかっている。これって《てーりょーてき》じゃないの？　数が出てるもん」

テトラ「ええ、そうなんですけど、ではその $1.013643{}264770{}5078125$ はどのくらいの小ささなのか……と思ったんです」

ユーリ「ほんとーは $1$ になってほしーけど、 $1.013643{}264770{}5078125$ になった。 てことは、 $$ 1.013643{}264770{}5078125 - 1 = 0.013643{}264770{}5078125 $$ がズレなんじゃないの？」

テトラ「それは引き算でいいんでしょうか？　もともとピタゴラスコンマ自体がズレを表しているんですよね」

ユーリ「えーと……そっか、 $1$ を $1.013643{}264770{}5078125$ から引き算するのは変？」

僕「うーん……引き算することは変じゃないよ。 たとえば実数 $x$ を $a$ 倍することと、 $b$ 倍することを比較したいとき、 $b - a$ に意味はあるかという話だよね。 $x$ を $b - a$ 倍した値 $(b - a)x$ は、《$ax$ に何を加えれば $bx$ が得られるか》に答える量になる」

ユーリ「なんですと？」

僕「簡単な話だよ。 $$ ax + (b - a)x = bx $$ だから、 $ax$ に $(b - a)x$ を加えれば $bx$ が得られる」

ユーリ「そゆことか」

僕「たとえば、 $a = 1, b = 1.013643{}264770{}5078125$ で、 $x$ は最初の音の周波数と考えれば、 ユーリの引き算は $b - a$ に相当するといえる」

テトラ「あ、あたしも混乱してきました。ピタゴラスコンマ自体がズレを表していますよね？」

僕「ズレを表すというと混乱するかもね。 ピタゴラスコンマは《最初の音の周波数 $x$ に何を掛ければ十三音目の周波数が得られるか》に答える量といえる。 数や量を得たときには、それが何なのかをよく理解しているのが大事だと思うよ」

テトラ「ああ……そうですね」

僕「特に《加える》のか《掛ける》のかの違いは大きい……そうか。これは対数が出てくる場面だなあ」

ユーリ「たいすう？」

僕「そうだよ。積がたくさん登場したり、比を考えたりする場面では対数が顔を出すことが多い」

ユーリ「なんで？　てか、対数って何だっけ」

対数の基本

僕「たとえば $10^3 = 1000$ という式が成り立つ。《$10$ の $3$ 乗は $1000$ に等しい》という」

ユーリ「うん」

僕「これと同じことを対数を使って《$10$ を底（てい）とする $1000$ の対数は $3$ に等しい》という。そして $\log$（ログ）という記号を使ってこう書く」

ユーリ「ろぐ」

僕「$1000$ から $3$ を得る計算を《$10$ を底として $1000$ の対数を取る》ということもある」

ユーリ「ゼロの数だ」

僕「そうだね。 $10$ を底にした場合には、 $10^n$ の $n$ はゼロの個数になるからね。 底は $10$ とは限らないし、 $10$ の冪乗以外の対数も取るからいつもゼロの個数とはいえないけど。 一般には、対数はこんなふうにいう」

ユーリ「そんで、音階でなぜに対数の話になったの？」

僕「対数は、積を和に変換するから」

ユーリ「ワニ変換！？」

僕「そんなに驚かなくてもいいよ。《対数は、積を和に変換する》性質がある。 簡単な例だと、 $$ 100 \times 1000 = 100000 $$ になるけど、これは、 $$ 10^2 \times 10^3 = 10^{2 + 3} $$ ということだね。掛け算をするんだけど、指数に注目すると足し算になってる」

ユーリ「掛け算すると、ゼロの個数は足し算になってる」

僕「そういうこと。いまはわかりやすいように $10$ の冪乗を出したけど、一般に、 $$ 10^{a} \times 10^{b} = 10^{a + b} $$ ということ。これは指数法則と呼ばれるものの一つ」

ユーリ「しすーほーそく」

僕「この式の意味は《$10^{a} \times 10^{b}$ は、 $10$ の $a + b$ 乗に等しい》ということ」

ユーリ「$10^{a} \times 10^{b} = 10^{a + b}$ だから」

僕「同じことだけど《$10$ を $a + b$ 乗したら、 $10^{a} \times 10^{b}$ に等しい》ともいえる」

ユーリ「そりゃそーだ」

僕「いまいったことを対数で書けば、 $$ \log_{10}{10^{a} \times 10^{b}} = a + b $$ となる」

ユーリ「えーと？　 $10$ を、 $a + b$ 乗したら、 $10^{a} \times 10^{b}$ に等しい……ほんとだ」

僕「だから、積を和に変換したいときには対数がよく出てくる。 指数の部分をメインで扱いたいときにも対数を使う。 僕は《上に乗っている指数を下に落とす》みたいな感覚で式変形しているなあ」

テトラ「あああああっ！　そういうことなんですねっ！」

僕「どうしたの、テトラちゃん急に」

テトラ「さっきあっちで見たパネルの意味がわかったからですっ！　セントという単位が出てきます」

セント

僕「なるほどね。《音は波》で、音の高さの違いは周波数の違い。 音の高さの違いを調べるときには、 $2$ 倍とか $3$ 倍とか $1/2$ 倍といった積に注目する。 だから、周波数 $x$ Hzと $y$ Hzの違いとして $y/x$ を調べたくなるのはわかる」

ユーリ「それじゃだめなの？割り算すればいいんでしょ？」