![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png)
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕：数学が好きな高校生。
ユーリ：僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕はユーリといっしょに、双倉図書館で開催されている《音楽と数学》というイベントに来ている（第283回参照）。
いまは《ピタゴラスの響き》コーナーで《ピタゴラス音階》を調べているところ。
音 $C$ から始めて、周波数を変えて音を作っていくのだが……
五個目の音 $E$
音 $A$ の周波数を $3/2$ 倍してできる音の周波数は、 音 $C$ の周波数を何倍すればいいでしょうか（第283回参照）。 その答えは、 $$ 27/16 \times 3/2 = 3^4/2^5 = 81/32 = 2.53125 $$ という計算で得られますが、 $81/32 > 2$ なので、 $1$ オクターブ下げるためにさらに $2$ で割ります。
音 $C$ の周波数を $81/64$ 倍した新しい音ができました。
$$ 81/64 = 1.265625 $$
新しくできた音を $E$ と呼びます。
$C$ と $G$ の組、 $G$ と $D$ の組、 $D$ と $A$ の組、 $A$ と $E$ の組は協和します。
私たちはこれで、 $C$ と $D$ と $E$ と $G$ と $A$ の五音を手に入れました。
ユーリ「五個の音だけでも、曲って作れるんだね（第283回参照）」
僕「そうだね。ここまでで $3/2$ 倍を繰り返して五音が出来たから、 同じことを続けていくんだろうけど……ユーリはそろそろ飽きてきたかな？」
ユーリ「やだなーおにいちゃんたらユーリはそんなにあきっぽくないしー」
僕「棒読みやめい……これが六個目の音だね」
僕とユーリは掲げられたパネルを見上げる。
六個目の音 $B$
音 $E$ の周波数を $3/2$ 倍してできる音の周波数は、 音 $C$ の周波数を何倍すればいいでしょうか。 その答えは、 $$ 81/64 \times 3/2 = 3^5/2^7 = 243/128 = 1.8984375 $$ という計算で得られます。
$243/128 = 1.8984375 < 2$ なので、初めの $C$ 音から $1$ オクターブの範囲に入っています。 ですからさらに $2$ で割る必要はありません。
音 $C$ の周波数を $243/128$ 倍した新しい音ができました。
新しくできた音を $B$ と呼びます。
$C$ と $G$ の組、 $G$ と $D$ の組、 $D$ と $A$ の組、 $A$ と $E$ の組、 $E$ と $B$ の組は協和します。
私たちはこれで、 $C$ と $D$ と $E$ と $G$ と $A$ と $B$ の六音を手に入れました。
ユーリ「飽きてこないけど、パターン見えてくるよね」
僕「パターンとは」
ユーリ「$3/2$ 倍して、 $2$ より大きくなったら $2$ で割る。その繰り返し。パターンじゃん？」
僕「そうだね。規則的に繰り返して音を作っていく。《ピタゴラス音階》を作っていく」
ユーリ「次のパネルはこれ？」
七個目の音 $F\#$
音 $B$ の周波数を $3/2$ 倍してできる音の周波数は、 音 $C$ の周波数を何倍すればいいでしょうか。 その答えは、 $$ 243/128 \times 3/2 = 3^6/2^8 = 729/256 = 2.84765625 $$ という計算で得られます。
$729/256 = 2.84765625 > 2$ なので、初めの $C$ 音から $1$ オクターブ上より高い音になります。 ですからさらに $2$ で割ります。
$$ 729/256 \times 1/2 = 3^6/2^9 = 729/512 = 1.423828125 $$
音 $C$ の周波数を $729/512$ 倍した新しい音ができました。
新しくできた音を $F\#$（エフシャープ）と呼びます。
$C$ と $G$ の組、 $G$ と $D$ の組、 $D$ と $A$ の組、 $A$ と $E$ の組、 $E$ と $B$ の組、 $B$ と $F\#$ の組は協和します。
私たちはこれで、 $C$ と $D$ と $E$ と $F\#$ と $G$ と $A$ と $B$ の七音を手に入れました。
僕「これで七音」
ユーリ「ねーねー、ユーリ発見したかも。パターン！」
僕「お？」
ユーリ「パネルにしつこく『私たちはこれで……を手に入れました』って書いてあるじゃん？ 作った順番が綺麗なパターンになってるよ！」
僕「どんなパターンだろう」
ユーリ「こんなの！ 見て見て！」
作られていく音の順番（ユーリの視点）
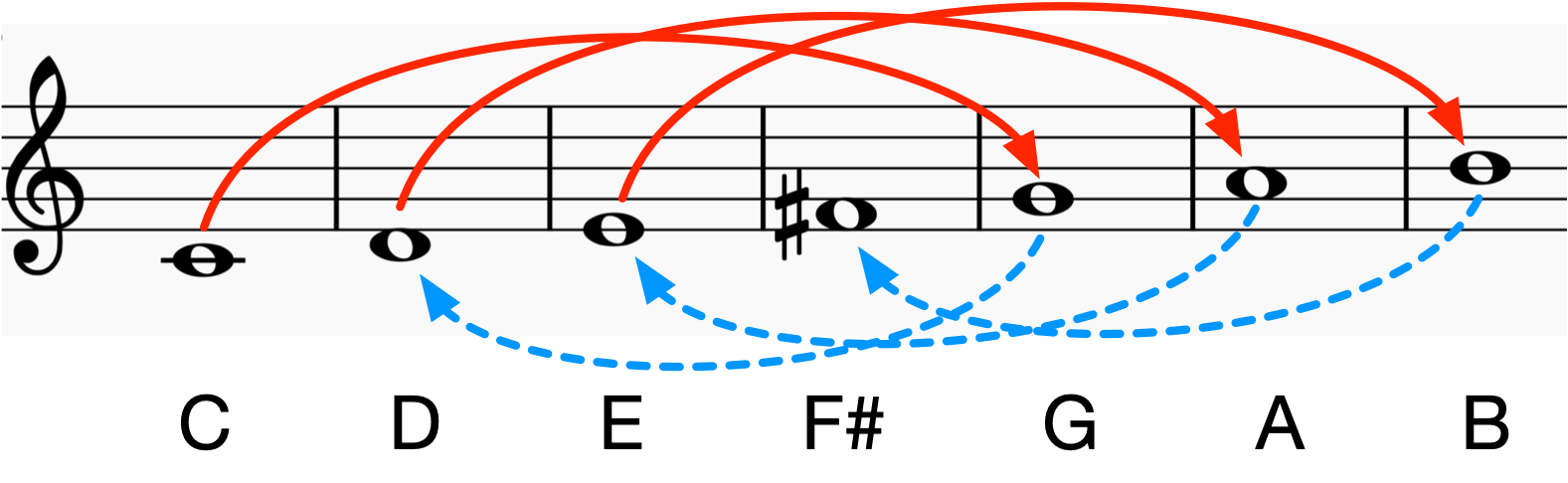
ユーリ「ね？ ね？ 下から順番に作られるんじゃなくて、上がって下がるのを繰り返すんだよ。何てゆーの……ぐるぐる？」
僕「ああ、ほんとだね。こんな風に行ったり来たりにも見える。ええと、それはなぜかというと……」
作られていく音の順番（僕の視点）
ユーリ「次のパネル行こ！ いよいよ八音目、到着だね！」
僕「おおい！」
八個目の音 $C\#$
音 $F\#$ の周波数を $3/2$ 倍してできる音の周波数は、 音 $C$ の周波数を何倍すればいいでしょうか。 その答えは、 $$ 729/256 \times 3/2 = 3^7/2^{10} = 2187/1024 = 2.1357421875 $$ という計算で得られます。
$2187/1024 = 2.1357421875 > 2$ なので、初めの $C$ 音から $1$ オクターブ上より高い音になります。 ですからさらに $2$ で割ります。
$$ 2087/1024 \times 1/2 = 3^7/2^{11} = 2187/2048 = 1.06787109375 $$
音 $C$ の周波数を $2187/2048$ 倍した新しい音ができました。
新しくできた音を $C\#$ と呼びます。
$C$ と $G$ の組、 $G$ と $D$ の組、 $D$ と $A$ の組、 $A$ と $E$ の組、 $E$ と $B$ の組、 $B$ と $F\#$ の組、 $F\#$ と $C\#$ の組は協和します。
私たちはこれで、 $C$ と $C\#$ と $D$ と $E$ と $F\#$ と $G$ と $A$ と $B$ の八音を手に入れました。
ユーリ「ありり？」
ユーリは、けげんな顔をして指を折り始めた。
僕「どんどん次のパネルに行くんじゃないの？」
ユーリ「これおかしくない？ $1$ オクターブって $8$ 音だよね？ ド・レ・ミ・ファ・ソ・ラ・シ・ド……ほら $8$ 音」
僕「そうだね。オクターブの名前の通り」
ユーリ「名前の通りって？」
テトラ「オクターブ（octave）の "oct-" というのは $8$ を意味するからですよね、先輩！」
僕「うわびっくりした！」
ユーリ「テトラさん！」
登場人物紹介（追加）
テトラちゃん：僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
僕「まるでミルカさんみたいに突然登場したね！」
テトラ「違いますよう！ さっき二人を見つけて追いかけていたんですけど、 急に走り出したりするので、なかなか追いつけなかっただけです。 人がいっぱいで……ところで、オクターブがどうしたんですか？」
ユーリ「あのね、 $1$ オクターブって $8$ 音だから、八個目の音を作ったら $1$ オクターブの音がぜんぶできると思ったの。でも、 $C\#$ になっちゃった」
僕「ああ、それで数を数えてたんだ……テトラちゃんはもう《ピタゴラス音階》のパネルはぜんぶ見たの？」
テトラ「あっ、はい。そうです。なのでネタバレにならないように黙っていますねっ！」
テトラちゃんはそう言って『口にチャック』のジェスチャをする。
ユーリ「テトラさん黙っちゃった……えーっと、 八個目で $C$ にならないってことは、もっと進まないと $1$ オクターブ上には行けないんだね。 $8$ 音よりも多くなるんだ」
僕「$F\#$ や $C\#$ も出てきたからね……ああ、そうだよ。 だって、ピアノの鍵盤を見ればわかる。 $1$ オクターブにあるキーは、 $8$ 個じゃなくて $12$ 個だ。黒鍵があるから」
ユーリ「あー、そだね。そんじゃ、 $3/2$ 倍を $12$ 回繰り返せばいーんだ！」
テトラ「あっ、それはっ……（チャック）」
僕「うん？ いや、おかしいよ、ユーリ。それは違うはずだ」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 440本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方／すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加（2020年2月14日）
![[icon]](https://img.hyuki.net/20220619121014-abd58cfc2ab436f4.png)