![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
ミルカさん:数学が好きな高校生。 僕のクラスメート。長い黒髪の《饒舌才媛》。
ミルカ「正 $6$ 面体群」
ミルカさんはそういって人差し指を立てる。
テトラ「正 $6$ 面体群……」
僕「名前があるんだ。そりゃそうか」
ミルカ「君とユーリが話していたのは、 正 $6$ 面体群の構造研究といえる。 ユーリは位数(いすう)を手がかりに《正 $6$ 面体群》と《$4$ 次の対称群 $S_4$》が同型であることを推測した……と、いえなくもない」
テトラ「正 $6$ 面体群に、位数に、 $4$ 次の対称群に……」
テトラちゃんは大急ぎでノートにキーワードをメモしている。
ミルカ「テトラは、以前学んだ群の定義を覚えている?」
テトラ「え、ええと……何となくは。単位元があって逆元がある計算ですよね」
僕「結合法則も必要だよ、テトラちゃん」
テトラ「あっ、そうでしたね。交換法則は……あったりなかったり」
ミルカ「心許ない。復習しよう」
ミルカ「いまから群の定義を復習する。群の定義に必要な用語を定義していこう」
ミルカさんはそう言って、 まるで手術を始める外科医のように、 手のひらを自分に向け肩の高さまで両手を上げた。
テトラ「はい」
ミルカ「まず、集合 $G$ を用意する。これは後ほど台集合と呼ばれることになる」
テトラ「質問です!」
ミルカさんが一言いった直後にテトラちゃんが質問の手を挙げた。早いな。
ミルカ「何?」
テトラ「できましたら、正 $6$ 面体群……ですよね。 その場合の例と合わせてお話しいただけますか。 そうすると、具体的に考えやすいので」
ミルカ「ふむ、なるほど」
ミルカさんは一瞬、目を閉じて考える。
ミルカ「正 $6$ 面体群ではサイコロのイメージが邪魔になるから、 もっと小さな例にしよう」
テトラ「あっ、いえっ、具体的なイメージがわかりやすい方がいいんですが」
ミルカ「いまから、例を出して具体的に話す。 しかし、サイコロのイメージがあると、群の定義を考えるにはイメージがむしろ邪魔になるという意味。 もっと抽象的な例の方がいい」
テトラ「抽象的な例……」
ミルカ「集合 $G$ としてこれを例に使おう」
集合 $G$ の例
$$ G = \SET{\AX,\BB,\CC,\DD} $$
テトラ「トランプのスートですね」
ミルカ「その $4$ 個が集合 $G$ の要素になる。集合 $G$ の元(げん)ともいう」
僕「$G$ を台集合と呼ぶのは、きっとこの集合 $G$ が群を作るときの土台となるものだからだよね」
テトラ「あっ、それ、次に質問しようと思っていましたっ!」
ミルカ「群に限らず、集合に構造を入れるときにその集合のことを台集合と呼ぶようだ」
テトラ「ここまで、理解しました。集合 $G$ を用意しました!」
ミルカ「次に二項演算(にこうえんざん)を用意する。 《集合 $G$ の要素二つの組》に対して、《集合 $G$ の要素一つ》を対応付ける。 名前がないと不便なのでその二項演算を $\MUL$ で表すことにしよう」
僕「集合 $G$ の要素 $a$ と $b$ の組に対して、 $$ a \MUL b $$ がまた集合 $G$ の要素になっている。積 $\MUL$ だね」
ミルカ「そういうこと。そのことを、 $$ \MUL : G \times G \to G $$ と表すこともある。 $\MUL$ は集合 $G \times G$ から集合 $G$ への写像だ」
テトラ「いまおっしゃっていた $a$ や $b$ は、たとえば $\AX$ や $\BB$ のことですね? では $\AX \MUL \BB$ というのは何でしょうか」
僕「$\AX \MUL \BB$ は、 $\AX$ と $\BB$ の組 $(\AX,\BB)$ に対して対応付けられた $G$ の要素を表しているんだよ、テトラちゃん」
テトラ「ですから、それは、いったい何でしょうか。 $\CC$ ですか、 $\DD$ ですか」
ミルカ「$\AX \MUL \BB$ が何に等しいかを定めているのが $\MUL$ という二項演算だ」
テトラ「イメージがわきにくいんですが、具体的には……」
僕「$\AX \MUL \BB = \CC$ かもしれないし、 $\AX \MUL \BB = \DD$ かもしれないし、 $\AX \MUL \BB = \AX$ かもしれないよ」
ミルカ「抽象的な例で、具体的に話そう。 演算表を提示すれば、二項演算が具体的に定まる」
演算表の例

僕「……」
テトラ「……」
僕「なるほど、そういうことか」
テトラ「えっ! これで何かわかるんですか?」
僕「この演算表の意味がわかったけど、 でも黙っていた方がいいよね。《知らないふりゲーム》だから」
テトラ「え……」
ミルカ「それはすごいな」
僕「(どうして棒読みなんだろう)」
ミルカ「ともかくこれで、二項演算 $\MUL$ が定義された。 テトラ、演算表の読み方は?」
テトラ「大丈夫……だと思います。たとえば、 この演算表を見ると、 $$ \AX \MUL \BB = \BB $$ だとわかります」
演算表から $\AX \MUL \BB = \BB$ がわかる
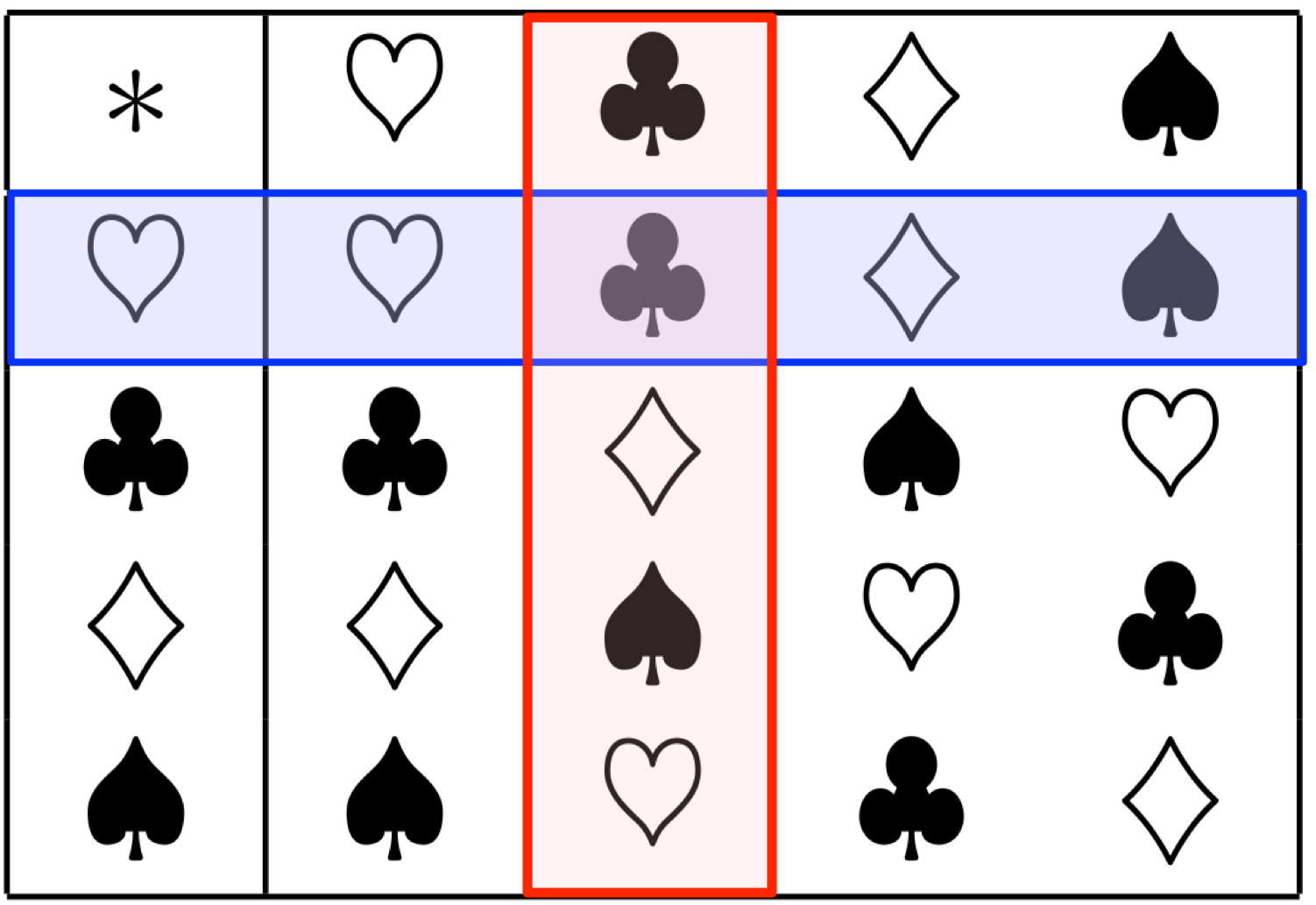
テトラ「他にはたとえば、 $$ \BB \MUL \BB = \CC $$ というのもわかります」
演算表から $\BB \MUL \BB = \CC$ がわかる

ミルカ「この演算表によって二項演算 $\MUL$ が定義されたとしよう。 二項演算 $\MUL$ は、 $$ \MUL: G\times G \to G $$ という写像と考えてもいい」
テトラ「さきほどもおっしゃっていましたが、 $G \times G \to G$ というのは何でしょうか」
ミルカ「$X$ と $Y$ が集合のとき、 $X \times Y$ を集合の直積という。 これは $X$ の要素 $x$ と $Y$ の要素 $y$ を組にした $(x,y)$ 全体の集合のこと」
集合の直積 $X \times Y$ $$ X \times Y = \SET{(x,y)\SETM x \in X, y \in Y} $$
ミルカ「$G \times G$ ならば、こうだ」
集合の直積 $G \times G$ $$ G \times G = \SET{(x,y)\SETM x \in G, y \in G} $$
テトラ「……」
僕「具体的に書くとこうだね」
集合の直積 $G \times G$

テトラ「わかりました。ダブルでわかりましたよ」
僕「ダブルって?」
テトラ「$G \times G$ という集合が何であるかがはっきりとわかりましたし、 ミルカさんが先ほどおっしゃっていた抽象的な例という意味もわかりました。 抽象的でも小さければ具体的に考えられるんですね」
ミルカ「彼が書いてくれたこの $G \times G$ は、 ちょうど演算表に対応させた書き方になっている。 ところで、 $$ \MUL: G\times G \to G $$ というのは、 《$\MUL$ は写像であり、 $G \times G$ の要素を一つ決めると、 $\MUL$ によって $G$ の要素が一つ決まる》 ということを表している」
テトラ「具体的にいえば、 $\MUL: (\AX,\BB) \to \BB$ のように対応がつくということですね」
ミルカ「そうなのだが、要素について具体的に述べるときには $\to$ という矢印ではなく $\mapsto$ という矢印を使うことが多い。 つまり、 $$ \MUL: (\AX, \BB) \mapsto \BB $$ のように書くということ」
テトラ「確認なんですが、それは、 $$ \AX \MUL \BB = \BB $$ と同じことをいってるんですよね?」
ミルカ「そうなる。 $\AX \MUL \BB = \BB$ という書き方は、 $\MUL$ を二項演算を行う演算子として見ていて、 $\MUL: (\AX, \BB) \mapsto \BB$ という書き方は、 $\MUL$ を写像として見ている。 さらにいうなら、 $\MUL(\AX, \BB) = \BB$ などと書いても意味はわかる。 しかし、表記が違うだけで主張していることは同じだ」
テトラ「理解しました! 抽象的な例というのはわかりやすいですね」
僕「そう?」
テトラ「そうです。今回、よくわかりました。 群のお話をお聞きするとき、あたしはいつもイメージで引っかかるんです。 この $\MUL$ というのは何だろうって」
ミルカ「二項演算」
僕「積だよね」
テトラ「その《積》という言葉もそうです。 つい数の掛け算と比べてしまうんです。 積というと、掛け算が持っているイメージがあって、 増えていくとか、面積になるとか……」
僕「積という言葉には意味はないと思うよ。 それこそ二項演算の代表として積という用語を使うだけで。 実際、交換法則が使える群のときには和と呼んだりするし」
テトラ「そうなんですよね……でも、 今回の $G = \SET{\AX, \BB, \CC, \DD}$ のように抽象的な、 計算とはまったく関係のない集合を考えますと、 イメージを抱きようがないので、かえって混乱しません」
ミルカ「テトラがいう《イメージ》とは《解釈》ともいえる。 集合の要素二つの組から、集合の要素一つを得る操作 $\MUL$ をどのように解釈したらいいかで悩むのだろう」
テトラ「解釈……確かに、そうかもしれません」
ミルカ「群の定義に戻ろう」
テトラ「はい……あっ、一点だけ。 先ほどの演算表は、あくまで例ですよね。これのことです」
演算表の例

ミルカ「その確認の意図を知りたい」
テトラ「他のように決めても構わないですよね。 この演算表ですと、 $$ \AX \MUL \BB = \BB $$ になりますけれど、 $\BB$ にならなくても、何か一つが決まれば《いい》んですよね。たとえば、 $$ \AX \MUL \BB = \CC $$ だとしてもかまわないですよね?」
僕「それは《まずい》んじゃないかな。それだと回転しすぎるし」
テトラ「回転?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2018年8月31日)