![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕とユーリはサイコロの置き方についておしゃべりをしている。
面を東西南北に向ける《サイコロの置き方が $24$ 通りあること》と、 《$4$ 個のものを並べる順列が $24$ 通りあること》の関係を調べているところ(第231回参照)。
サイコロの回転軸を工夫することでいったん納得した(第232回参照)。でも……
ユーリ「いやー、うまく行くもんだねー。回転を考えると $24 = 4 \times 3 \times 2 \times 1$ が出てきてすっきりした!」
$3$ 種類の回転軸

僕「うん、それはユーリが《わからない》と言い続けてくれたからだよ。 だから、すっきりした説明を探すことができたんだ。ただ……気になることがある」
ユーリ「へ? まだ?」
僕「うん。頂点の名前の付け方が気になっている」
ユーリ「$A,B,C,D,A',B',C',D'$ でしょ?」
僕「そうなんだけどね。僕たちは、立方体の置き方が $24$ 通りあるということを調べている。 ユーリは $24 = 4 \times 3 \times 2 \times 1 = 4!$ になるということに気付いた。 だから、《サイコロの置き方》を《$A,B,C,D$ という $4$ 個のものの順列》で表現できないかと考えていた」
ユーリ「だから、それ、確かめたじゃん。お兄ちゃんが言ったんだよ。机の上に接する頂点 $4$ 個の並び替えだと思えばいいって」
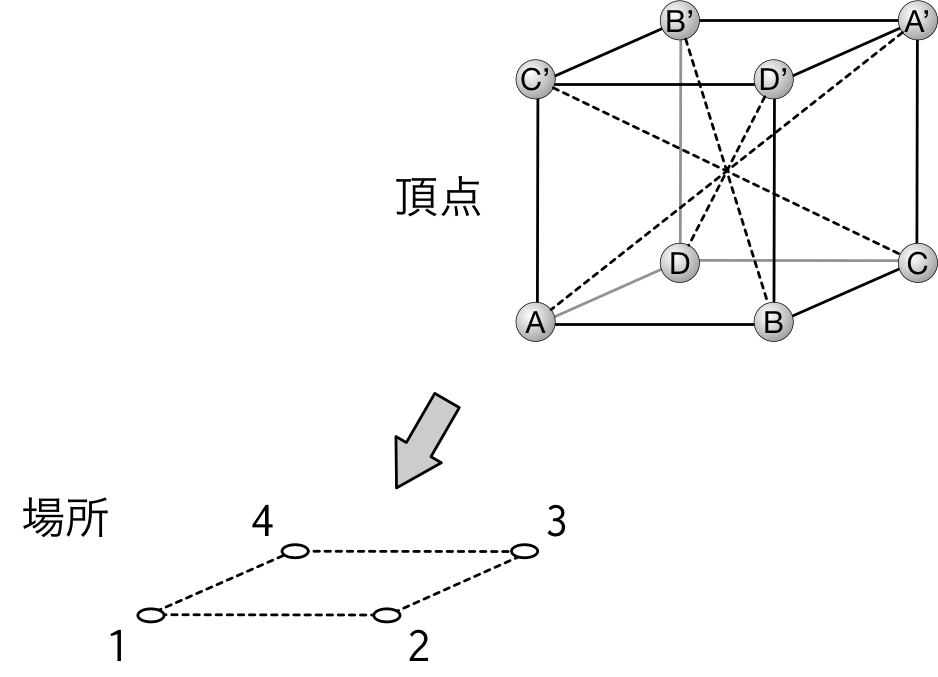
僕「ちょうど対角線の位置にある点の組を $A$ と $A'$ のように名前を付けたけど、 それがどうも気になるんだよ。ご都合主義っぽくて」
ユーリ「……」
僕「……」
ユーリ「うーん……お兄ちゃんは何を気にしてるの?」
僕「もっと、もっと明確に《$4$ 個のものの順列》を確かめたいということ」
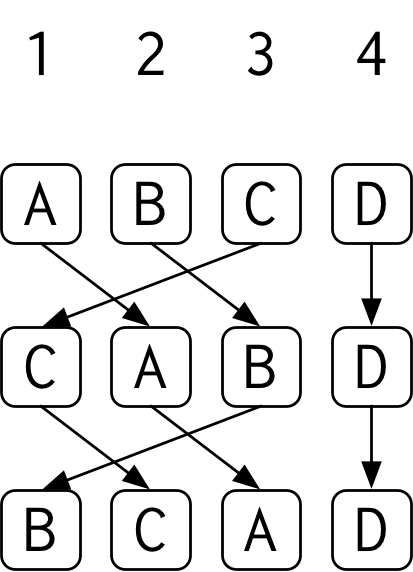
ユーリ「机の上に $1,2,3,4$ という $4$ つの場所があって、そこに $A,B,C,D$ という $4$ 個のものを並べて置くだけじゃなく?」
僕「そういうこと」
ユーリ「$4$ つの場所に $4$ 個のものを置けばいいんだよね?」
僕「その通り! お、ユーリは何かいいアイディアがあるの?」
ユーリ「ない」
僕「なんだ」
ユーリ「でもさー、立方体なんだから、面か、辺か、頂点しかないじゃん?」
僕「……いや、ちょっと待った」
ユーリ「さっきから待ってんだけど」
僕「対角線を並べ替えるというのはどうだろうか。 そうだよ!最初からわかってたことじゃないか。 $A$ と $A'$ という対角線の位置にある二つの頂点を同一視するって!」
ユーリ「対角線を並べ替える……って意味わかんない」
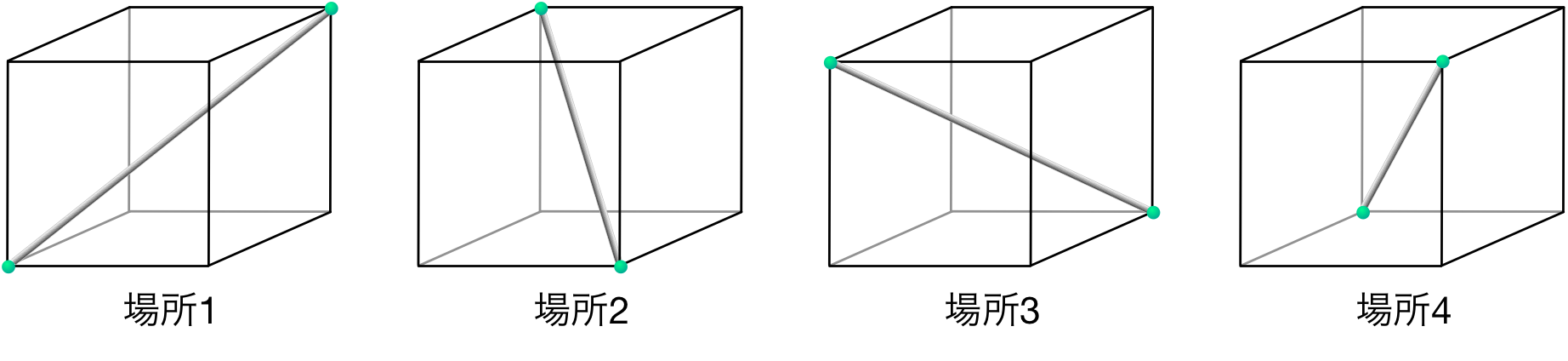
僕「立方体の対角線は全部で $4$ 本あるよね。ここでは、立方体の中央を通る対角線のことだよ。 立方体の置き方をどう変えても、 $4$ 本の対角線が来る場所はいつも決まっている。 だから、そこを《対角線が来る $4$ つの場所》として $1,2,3,4$ と番号を付ける」
対角線が来る $4$ つの場所 $1,2,3,4$
ユーリ「おー……」
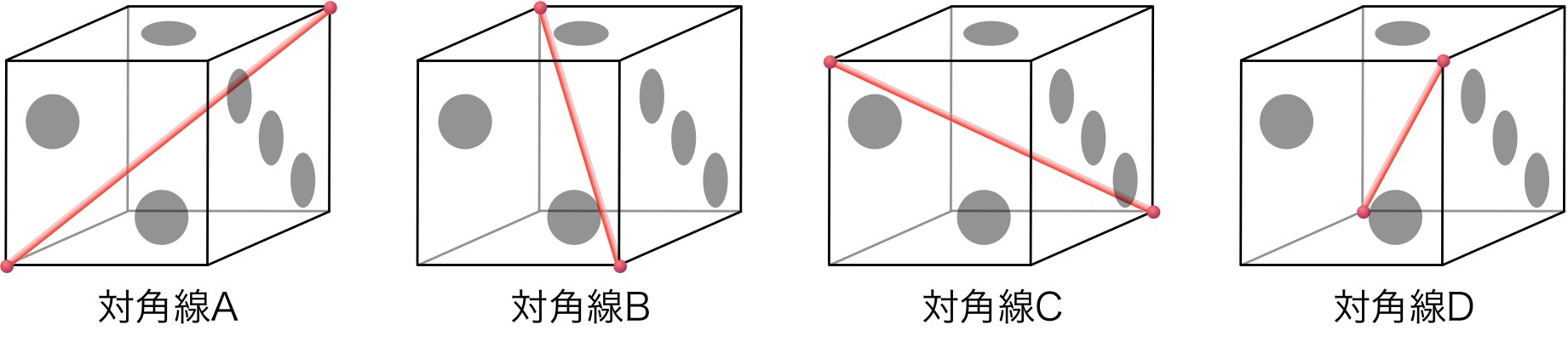
僕「そして、具体的なサイコロの $4$ 本の対角線に $A,B,C,D$ と名前を付ける。 うん、これでうまくいく!対角線上にある二つの頂点 $A,A'$ を結ぶ線分を考えることは、うまいこと同一視してることになるんだ!」
$4$ 本の対角線 $A,B,C,D$
ユーリ「えーと?」
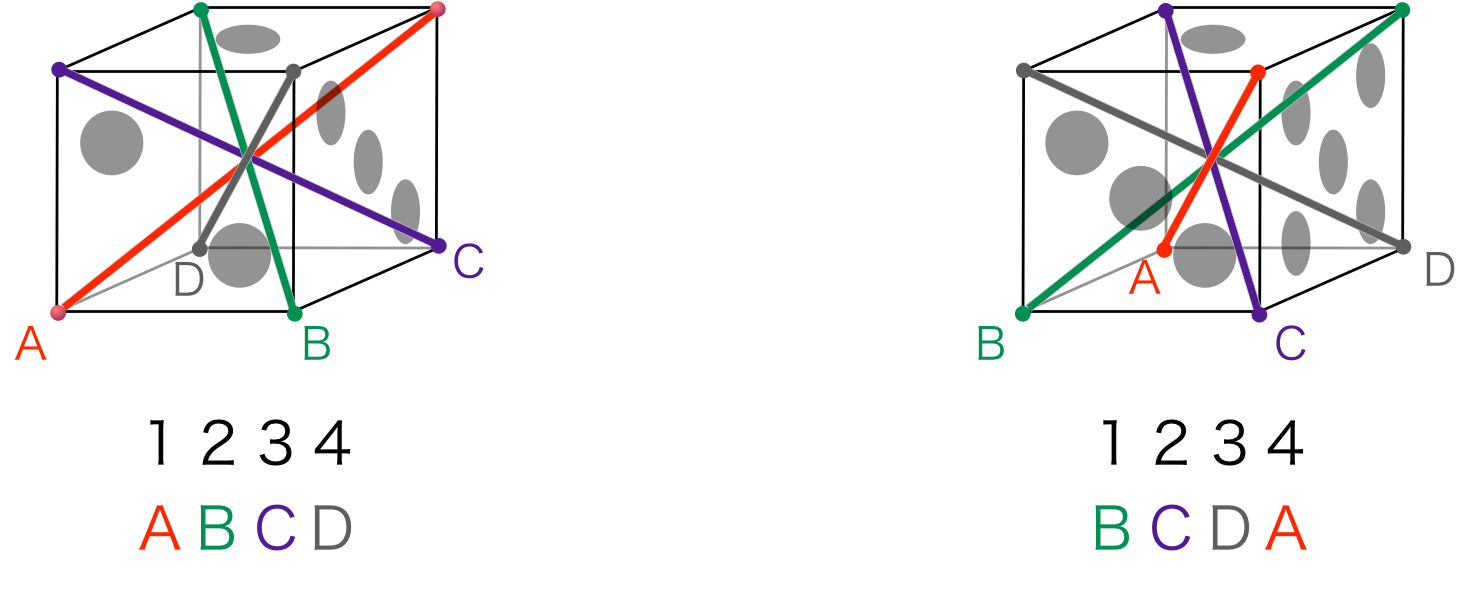
僕「場所 $1,2,3,4$ のそれぞれに、対角線 $A,B,C,D$ のどれが来るかを考えるということだよ。 たとえば、 $1,2,3,4$ に $A,B,C,D$ が来る置き方を $ABCD$ と呼ぶし、 $1,2,3,4$ に $B,C,D,A$ が来る置き方を $BCDA$ と呼ぶことにしよう」
$ABCD$ の置き方と、 $BCDA$ の置き方
僕「うん、これで心置きなく、 $\prime$ の記号を取り除くことができる。 $4$ つの場所 $1,2,3,4$ に対して、 $4$ 本の対角線 $A,B,C,D$ のどれがやって来るかを考える。 サイコロの $24$ 通りの置き方には、 $A,B,C,D$ の順列によって名前を付けることができるんだ!」
サイコロの置き方 $24$ 通りと、対角線の並べ方の名前付けの対応表
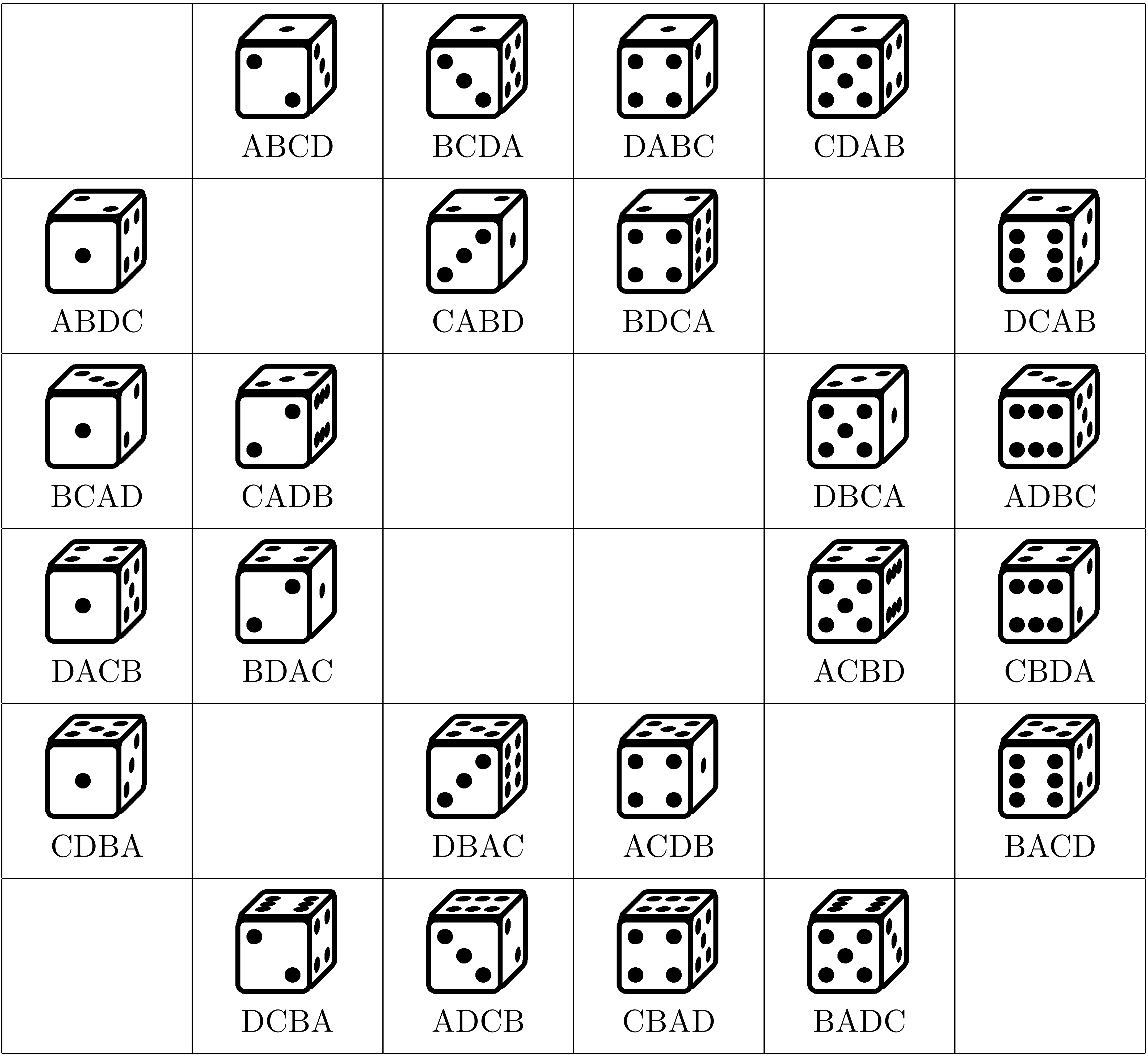
ユーリ「あたりまえだけど……不思議だにゃあ。 回転の軸のことを考えるとうまいこと $24$ 通りになるのはあたりまえだけど、 この表を見てると不思議。うまいこと、ぴったり、はまる。それが不思議」
僕「そうだねえ」
ユーリ「はっ!! ねねね、お兄ちゃん。回したらどーなるの?」
僕「何を回すって?」
ユーリ「サイコロを回転軸で回すと、この対応表でジャンプするわけじゃん? 回転軸が変わるとジャンプ先が変わるよね。どんな形がでてくる?」
僕「なるほど、それはおもしろそうだな。たとえば、 $ABCD$ をひとつの対角線でまわすと、 $$ ABCD \to CABD \to BCAD \to ABCD \to CABD \to BCAD \to \cdots $$ とジャンプするね。 $ABCD,CABD,BCAD$ を結ぶ三角形だ」
ユーリ「え、どれどれ? ちゃんと表に描いてよー」
僕「こういう三角形になるということ」
$ABCD,CABD,BCAD$ を結ぶ三角形
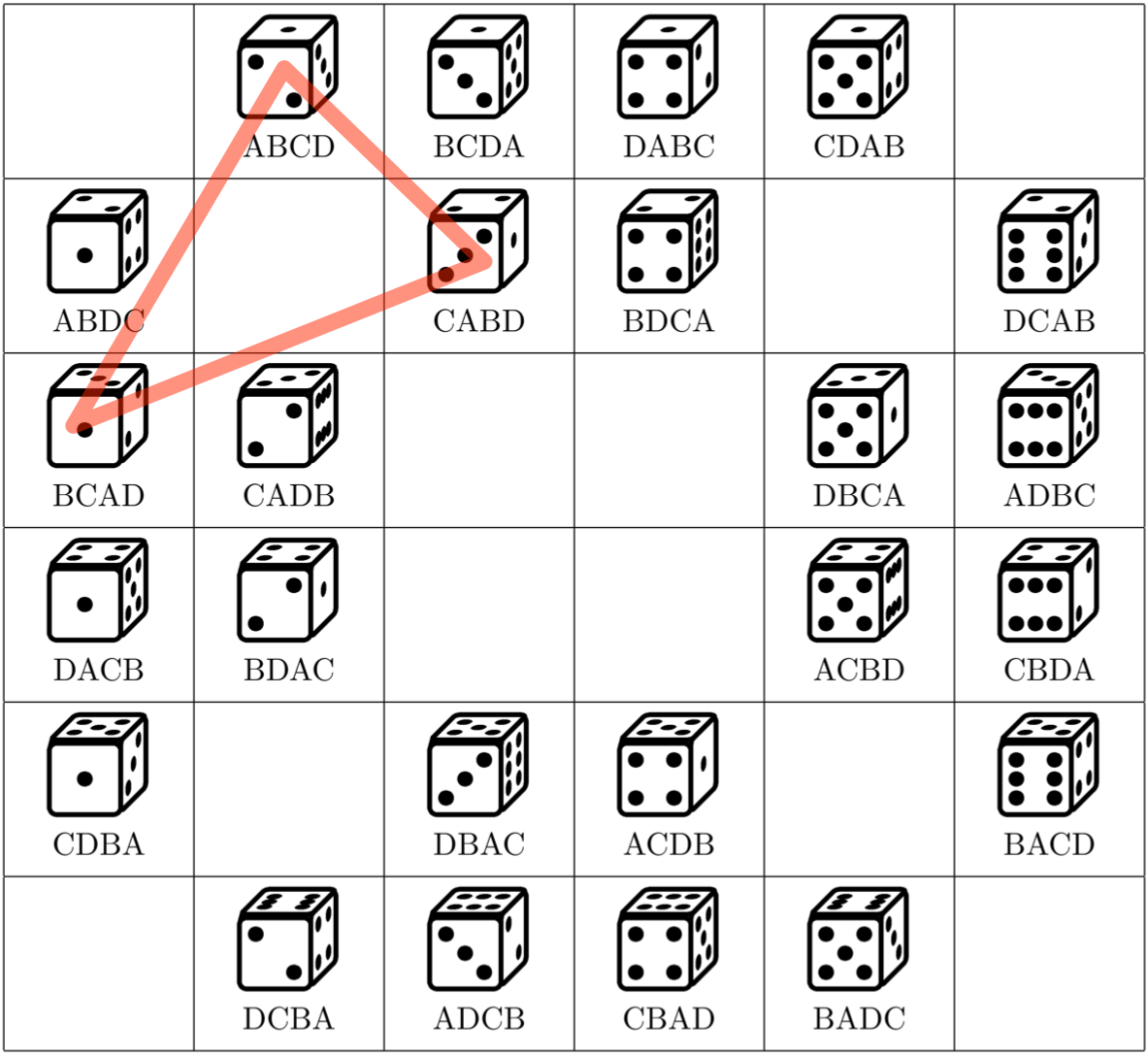
ユーリ「ほほー……これって、対角線 $D$ を回転軸にした場合だね?」
僕「そうだね。対角線 $D$ を回転軸にしたともいえるし、場所 $4$ にある対角線を回転軸にしたともいえる。 うん、回転軸になっている $D$ は場所 $4$ から動かない。 $D$ は動かないで、 $A,B,C$ が順にズレていってる」
$$ \UL{ABC}D \to \UL{CAB}D \to \UL{BCA}D \to \cdots $$
ユーリ「ふんふん。 $ABCD$ から始めたからこーゆー三角形だけど、隣の $BCDA$ から始めて、場所 $4$ にある対角線 $A$ で同じことやったら、 別の三角形になるよね」
僕「そうだね!今度は $A$ が場所 $4$ から動かないで、 $B,C,D$ が順にズレていくはず」
$$ \UL{BCD}A \to \UL{CDB}A \to \UL{DBC}A \to \cdots $$$BCDA,CDBA,DBCA$ を結ぶ三角形

ユーリ「そして次は……」
こんなふうにして僕たちは場所 $4$ にある対角線を回転させたようすを対応表に描いていった……
僕「できたできた……」
場所 $4$ の対角線で回転
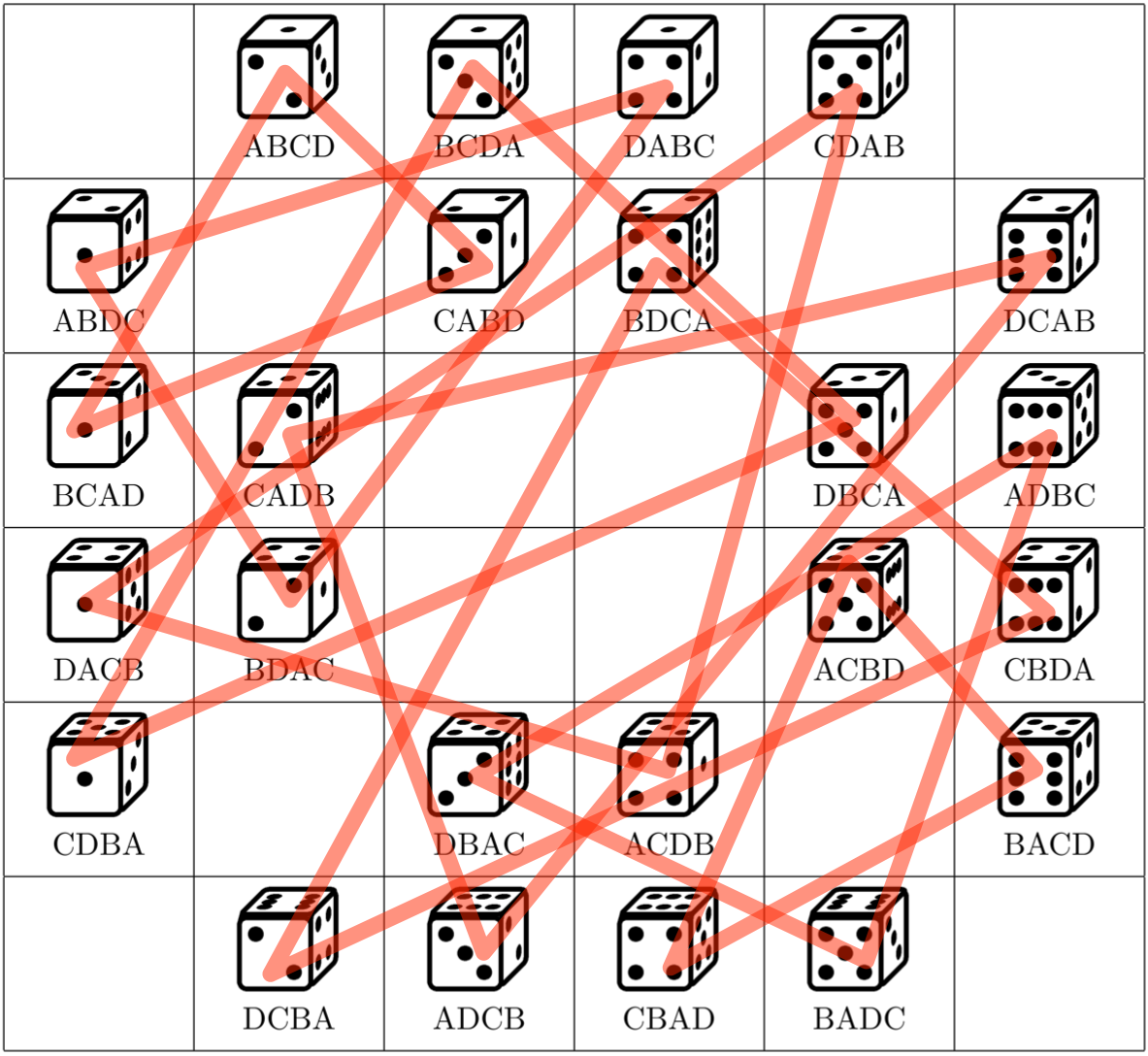
ユーリ「できたけど……図に描けばわかりやすくなるわけでもないね!ごちゃごちゃしただけじゃん! こないだテレビでやってた『シン・ゴジラ』にこういう図出てこなかったっけ」
僕「ゴジラの構造解析図だね!……おほん、時事ネタ自重。確かにごちゃごちゃしてるけど、対称性はあるね」
ユーリ「対称性って?」
僕「つまりね、でたらめに線が引かれているわけじゃないってこと。たとえば、 $$ \UL{ABC}D \to \UL{CAB}D \to \UL{BCA}D $$ の三角形とちょうど線対称の位置に、 $$ \UL{BAC}D \to \UL{ACB}D \to \UL{CBA}D $$ という三角形が描かれている。どちらも対角線 $D$ が動かない三角形だね」
対角線 $D$ が場所 $4$ から動かない三角形二つ

ユーリ「ほんとだ……」
僕「他の三角形たちも、ペアがいるよ」
対角線 $A$ が場所 $4$ から動かない三角形二つ

対角線 $C$ が場所 $4$ から動かない三角形二つ
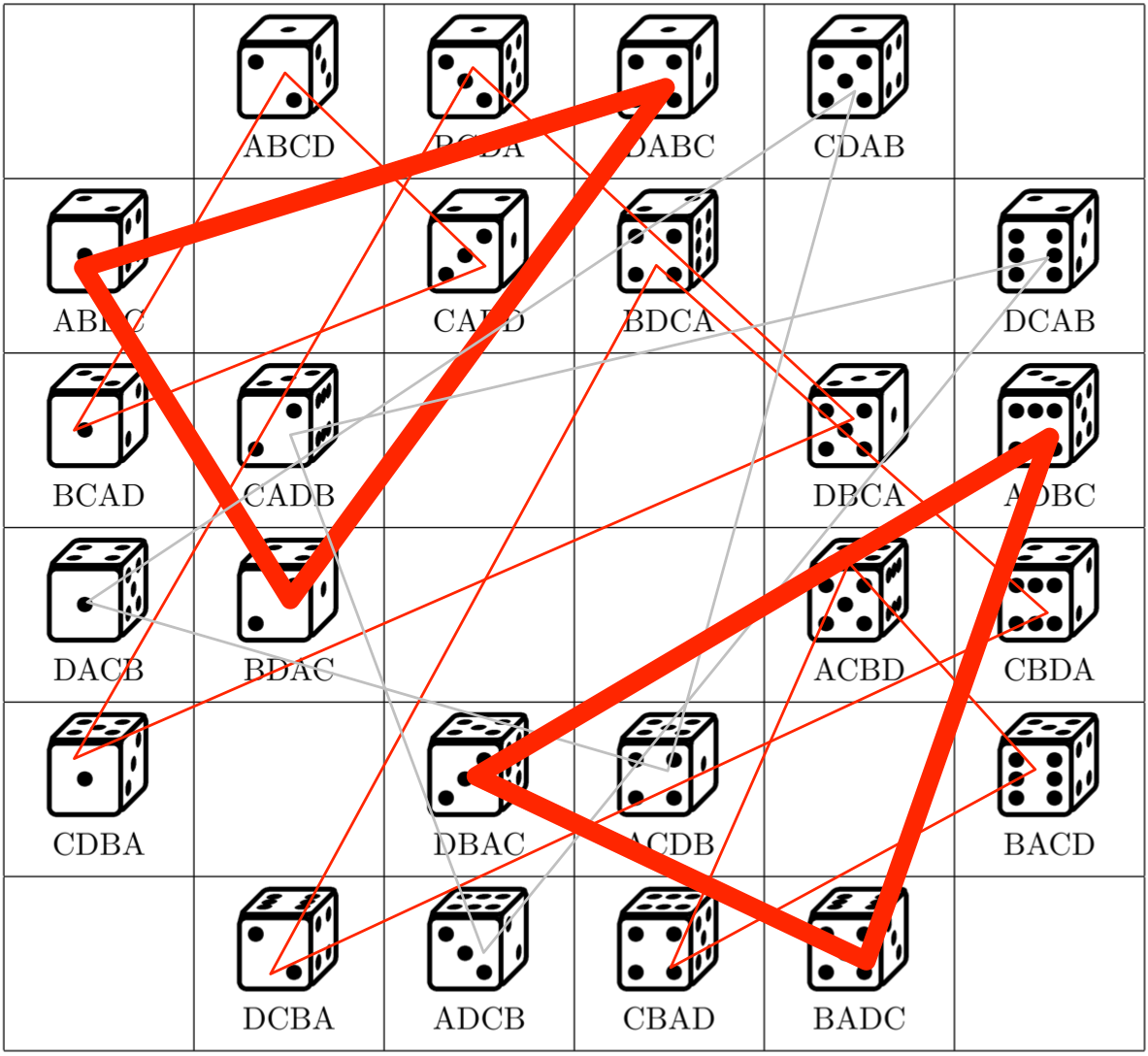
対角線 $B$ が場所 $4$ から動かない三角形二つ

ユーリ「あっ、これって《左手の世界》と《右手の世界》だね(第232回参照)。 この二つの三角形は、サイコロをこっちから見るか、むこうから見るかの違い?」
僕「そういうことだねえ。あ、じゃあクイズ。 この二つの三角形を行き来するにはどういう回転をしたらいい?」
ユーリ「行き来するって意味がわかんない」
僕「そうか。もっと正確にいうと、 $ABCD$ という置き方から、 $BACD$ という置き方にジャンプするにはどういう回転になる?」
クイズ
$ABCD$ という置き方から、 $BACD$ という置き方にジャンプするには、サイコロをどう回転すればいいか。
$$ ABCD \to BACD $$
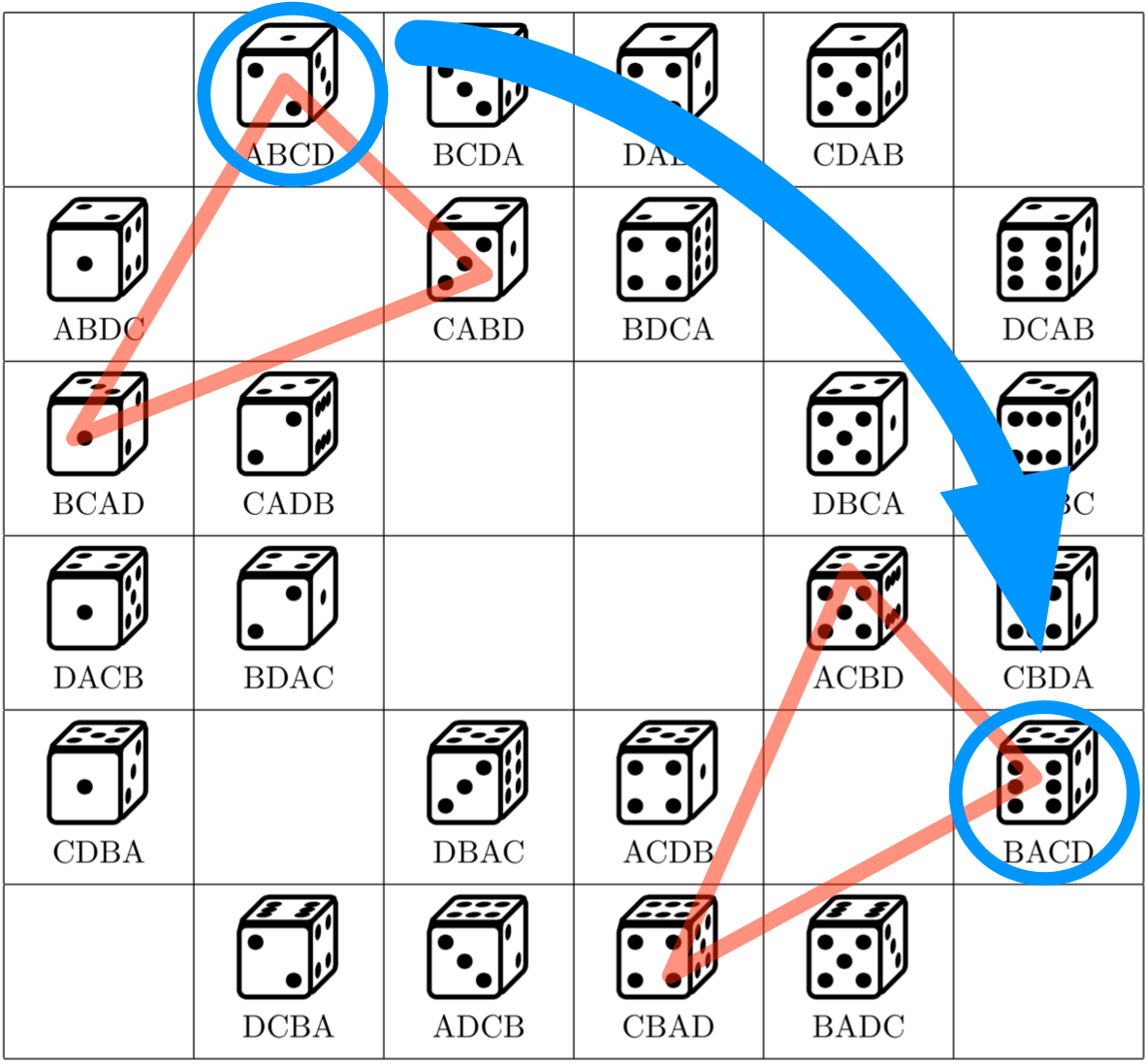
ユーリ「むむむ……」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2018年8月17日)