第225回 シーズン23 エピソード5

最小上界を求めて（前編）

僕「ちょうどいま、ロルの定理の証明が終わったところなんだよ（第224回参照）」

テトラ「証明の流れがおもしろかったです」

• 平均値の定理を、ロルの定理に帰着させます。
• ロルの定理のうち、定数関数についてはすぐに証明できます。
• ロルの定理のうち、最大値を取らない関数については上下反転させることで最大値を取る関数に帰着して証明できます。
• 残っているのは、最大値を使ってロルの定理を証明することです。
• 最大値であるという性質と微分係数の存在を使って証明ができました。

ミルカ「ふうん……これはこれで楽しいけれど、もう一歩踏み込もう」

僕「もう一歩って？」

ミルカ「ここまでで証明できたことは、 もし $g(x)$ が $a < x < b$ で最大値を取るならば、 ロルの定理が成り立つということだ」

テトラ「最大値を取らない関数については上下反転させて考えることにしたんですが……」

ミルカ「そういう話ではない」

僕「どういう話なんだろう」

ミルカ「こういう話」

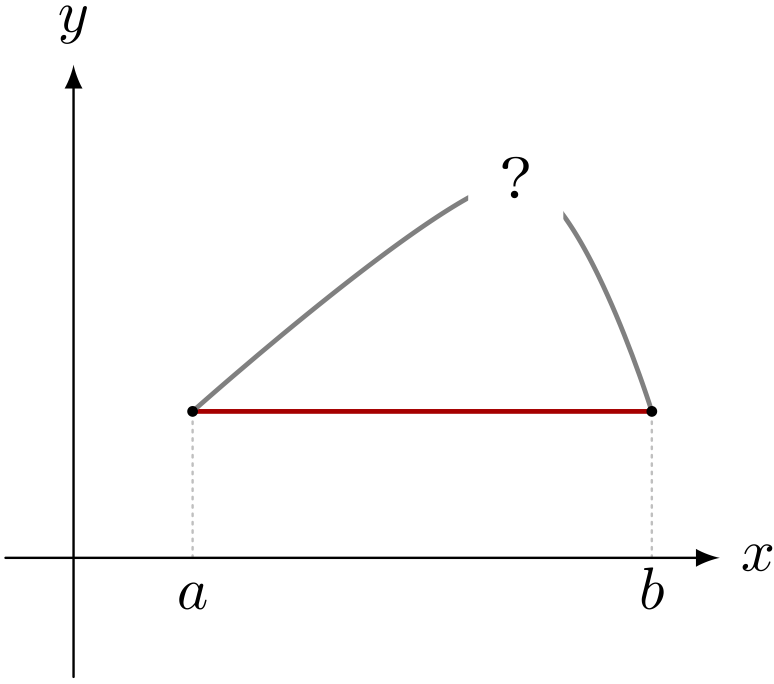
ミルカ「君が関数 $g(x)$ についてロルの定理を証明するときに、 $a < x < b$ で最小値か最大値を取るということを暗黙のうちに使っている。 だとしたら、残るピースはこれだ」

僕「これは……あたりまえじゃないんだろうか」

テトラ「あたりまえに見えるものを証明するって……難しいです」

ミルカ「ロルの定理から出発したからごちゃごちゃと条件をつけたけれど、言いたいことはずっと単純化できる。 閉区間 $[a,b]$ から実数全体の集合への連続な関数 $f(x)$ はこのような性質を持つという主張だ」

テトラ「閉区間……」

ミルカ「閉区間 $[a,b]$ とは、 $a \LEQ x \LEQ b$ を満たす実数 $x$ 全体の集合のこと」

僕「これがポイントだというのはわかるよ。 $x = a$ と $x = b$ で関数の値が等しいという条件は平均値の定理をロルの定理に帰着させるためにつけた条件だし」

テトラ「先輩方、ちょっとお待ちください。 閉区間 $[a,b]$ で連続な関数 $f(x)$ が最大値および最小値を取るという主張の意味を確かめたいんですが、 たとえば $y = f(x)$ のグラフを描くと、 必ず最大値 $\max$ と最小値 $\min$ があるということですよね？」

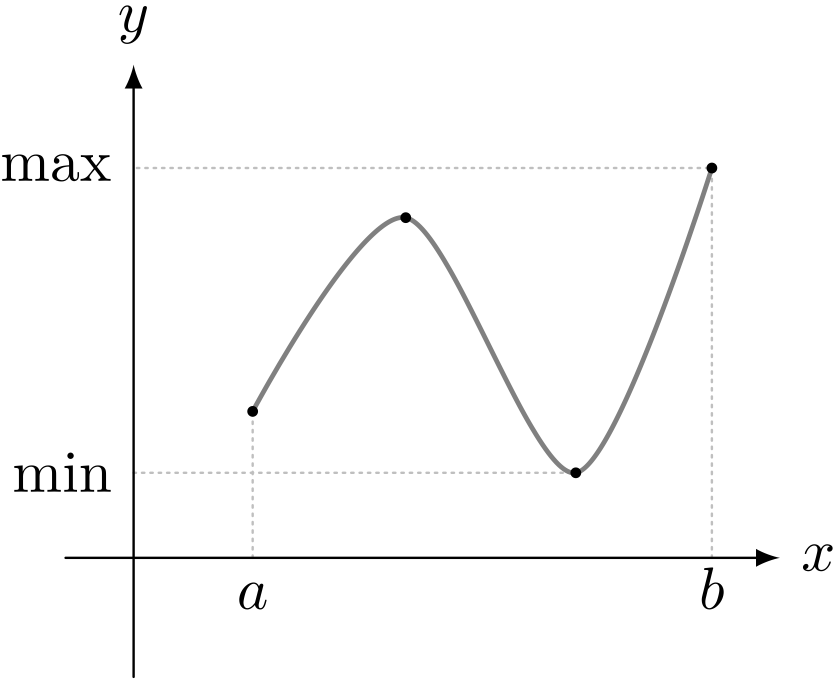
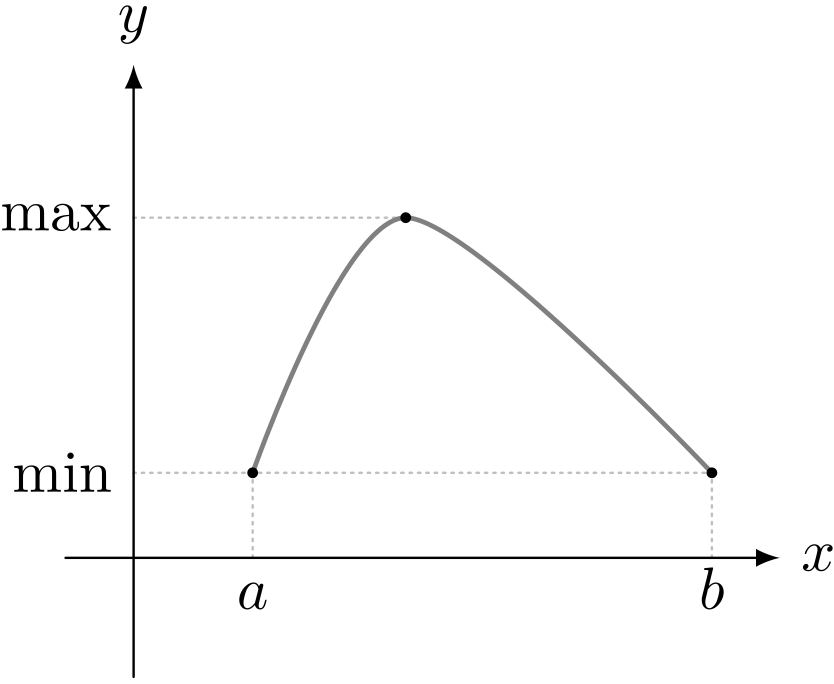
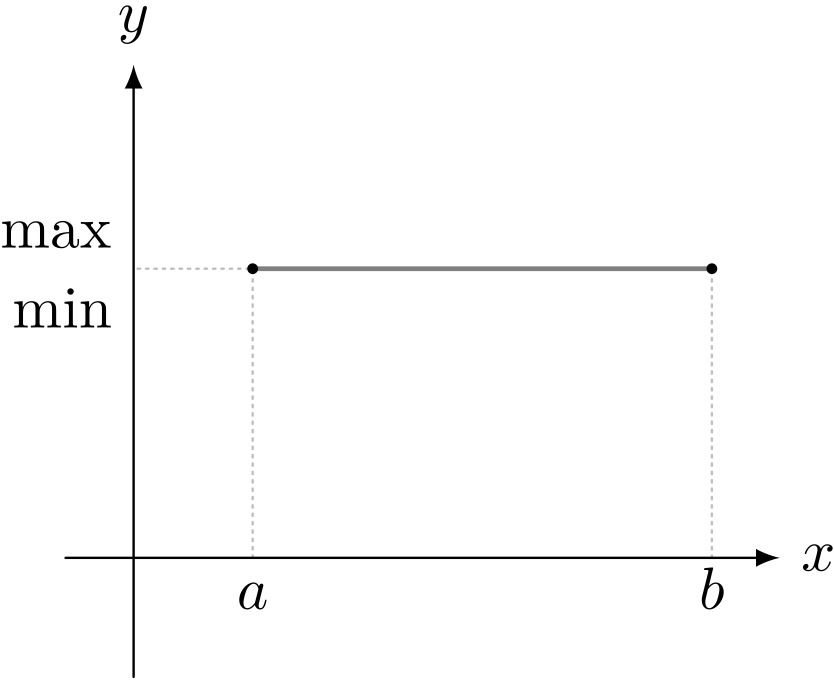
僕「そうだね」

テトラ「だとしたら……やっぱり《あたりまえ》だと思うんです。だって、 $f(x) = \infty$ というのはありえないですよね。 だって、 $\infty$ は数じゃありませんから。グラフで上の方……無限までどおおんと吹き抜けることはできないです。 だったら、必ず最大値があるはずじゃないでしょうか。グラフで考えれば《あたりまえ》です」

ミルカ「グラフで考えるのは大事だが、いま問題にしようとしているのはそこに隠れている条件のことだ」

テトラ「グラフに何か隠れているんですか？」

ミルカ「たとえば、このようなグラフを考えよう」

テトラ「はい。この場合は最大値は $1$ で、最小値は $0$ になります。 最大値を取るのは $x = \SQRT{2}$ のときで、 最小値を取るのは $x = a$ または $x = b$ のときになります」

ミルカ「もちろん、テトラのその答えで正しい。 だがもし仮に、関数 $f(x)$ の定義域が $a \LEQ x \LEQ b$ を満たす有理数全体の集合だとしたらどうだろうか」

僕「なるほど。 $x$ の取り得る値を、実数じゃなくて有理数に制限するということ？」

テトラ「有理数に制限……それは、 $x = \SQRT{2}$ にはならないということですね？」

ミルカ「その場合、 $f(x)$ の最大値は $1$ であるとはいえなくなる。 なぜなら、 $x = \SQRT{2}$ にはならないからだ」

テトラ「ええと、でも、その場合は $f(x)$ の最大値は何になるんでしょうか」

ミルカ「最大値は存在しない」

テトラ「最大値は存在しない！　……で、でも、 $f(x)$ は $1$ より大きくはならないですよ？　それはグラフで考えればわかります」

ミルカ「最大値の定義は？　 $a \LEQ x \LEQ b$ における $f(x)$ の最大値とは何か」

テトラ「最大値は、一番大きな値ですよね。 ですから、 $a \LEQ x \LEQ b$ の $x$ に対して、 $f(x) \LEQ M$ になる実数 $M$ のことです……よね？」

ミルカ「違う」

テトラ「違う？！」

ミルカ「テトラがいま言った実数 $M$ は $f(x)$ が取り得る値の最大値ではなく、 $f(x)$ が取り得る値の上界（じょうかい）というものになる」

テトラ「上界……」

僕「$f(x)$ の値が $M$ 以下になるというだけじゃなくて、 $f(x) = M$ になるような $x$ が存在しなくちゃ最大値とはいえないからだよ、テトラちゃん。

テトラ「ああ……」

ミルカ「こういうときこそ、論理式が役に立つ。私たちがふだん使っている言葉では細かい差違が明確にならないとき」

テトラ「……なるほどです。あたしは頭の中では最大値のことを考えながら、上界の定義を話していたことになりますね」

ミルカ「上界は一つとは限らないことに注意」

テトラ「あ、はい、わかります。 $M$ 以上の数はぜんぶ上界になるからですね？」

僕「そうだね」

テトラ「でも、最大値は一つですよね？」

ミルカ「最大値は、存在すれば一つに限る。証明はすぐできる」