第224回 シーズン23 エピソード4

平均値の定理（後編）

平均値の定理をどうやって証明する？

テトラ「でも、条件って……これだけですよね？」

• 二つの実数 $a,b$ は、 $a < b$ を満たす。
• 関数 $f(x)$ は、 $a \LEQ x \LEQ b$ で連続である。
• 関数 $f(x)$ は、 $a < x < b$ で微分可能である。

僕「そうだね。これだけ。これだけで証明できる。 これだけといっても、連続や微分可能というのはとても強い条件だよ」

テトラ「どんな証明になるのか、まったく想像が付きません……先輩は証明をご存じなんですよね？」

僕「うん、うろ覚えだけど以前やったことがあるよ」

テトラ「平均値の定理の証明、教えてください。よろしくお願いします、先輩！」

僕「こんなふうにして、僕たちの旅が始まった。 このときには、未来にどんな困難が待ち受けているのか二人とも想像できなかったのだ……」

テトラ「はい？」

僕「いやいや独り言。証明を少しずつ思い出すから、ゆっくりいっしょに行こう」

テトラ「はいっ！」

僕「平均値の定理の証明は、まず最初に関数 $f(x)$ を単純化するところから始めよう。 《両端の関数値が等しい》という条件を付けてやるんだよ。つまり、 $f(a) = f(b)$ という条件で考えることにする。 そうすると、 $f(b) - f(a) = 0$ になるから、証明すべきことがシンプルにできる。 $f'(c) = 0$ になる $c$ を見つければいいということだから」

テトラ「えっ？　そんな勝手な条件をつけてもいいんでしょうか。 そのようなことをしたら、平均値とは違う定理を証明したことになってしまいますよね」

僕「そうなっちゃうね。 関数 $f(x)$ に条件を付けた平均値の定理は、ロルの定理っていうんだ。 だから、平均値の定理とロルの定理のあいだはちゃんとつないでやる必要がある」

テトラ「つなぐ？」

僕「うん、ちゃんと順序を追って説明するよ。混乱しないようにロルの定理で証明する関数の方は $g(x)$ という別の名前をつけておくね」

テトラ「なるほど……意味はわかります。 平均値の定理で証明すべきことは、両端点を結んだ線分と平行な接線が引けるということでした。 ロルの定理で証明すべきことは、水平な接線が引けるということですね？ $g'(c) = 0$ は接線が水平ということですから」

僕「そういうこと。 $g(a) = g(b)$ のとき両端点 $(a,g(a))$ と $(b,g(b))$ を結んだ線分は水平だから、 水平な接線が引けるなら、線分と接線は平行になってることになる。 つまりロルの定理は、平均値の定理の特別な場合ということだね」

テトラ「でも、 $f(x)$ と $g(x)$ は違うものですよね」

僕「うん、そうだね。平均値の定理とロルの定理は別の定理。 でも、ロルの定理が証明できれば、そこからすぐに、平均値の定理も証明できるんだ」

テトラ「へ、へえ……そうなんですか。そういう感覚は想像が付きません」

僕「だって、平均値の定理に出てくる $f(x)$ が与えられたなら、 そこから $g(a) = g(b)$ を満たすような $g(x)$ はすぐに作れるよ」

テトラ「$g(x)$ を……作る？」

僕「だって、 $$ y = f(x) $$ のグラフを、 $$ y = \frac{f(b) - f(a)}{b - a}(x - a) $$ のグラフの分だけ下げてやるだけでいいからね。 引き算して、こんな $g(x)$ を作ればいいんだ」

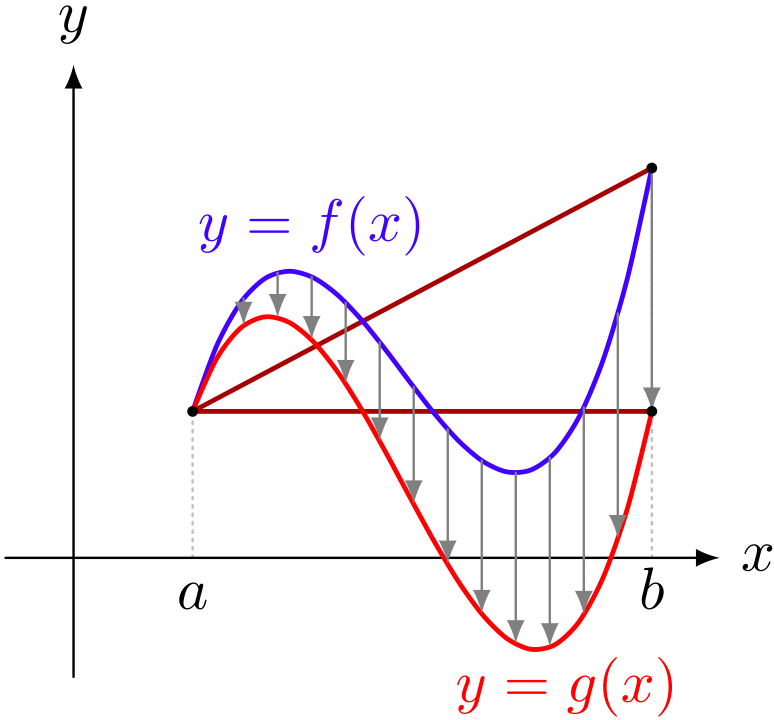
テトラ「ははあ……」

僕「こんなふうに $g(x)$ を作れば、 $g(a) = g(b)$ という式になっていて、 しかも $f(x)$ の連続性や微分可能性が、そのまま $g(x)$ にも引き継がれる。 平均値の定理で与えられている条件を持つ $f(x)$ があったとしたら、 その $f(x)$ から $g(x)$ を作る。 そしてその $g(x)$ についてロルの定理を証明する。 そのときに存在が証明された $c$ を使って、 $f(x)$ について平均値の定理が証明できたことになる」

テトラ「そう……なりますか？」

僕「なるよ。だって、 $$ g(x) = f(x) - \frac{f(b) - f(a)}{b - a}(x - a) $$ を $x$ で微分してみよう。そうすると、 $$ g'(x) = f'(x) - \frac{f(b) - f(a)}{b - a} $$ になるよね。 $g'(x)$ の $x$ に $c$ を代入すると、 $$ g'(c) = f'(c) - \frac{f(b) - f(a)}{b - a} $$ になる。 もしもこの $c$ が、ロルの定理で $g'(c) = 0$ が成り立つような $c$ だとしたら、右辺も $0$ に等しくなる。 つまり、 $$ f'(c) - \frac{f(b) - f(a)}{b - a} = 0 $$ が成り立つということ。 こういう $c$ が存在するといえるなら、 $$ f'(c) = \frac{f(b) - f(a)}{b - a} $$ が成り立つ $c$ が存在するといえる。そしてそれが平均値の定理の証明で言いたかったこと」

テトラ「な、なるほどです！」

僕「だから、ロルの定理を証明しさえすれば、平均値の定理が証明できたことになる」

テトラ「そんなふうに $f(x)$ から $g(x)$ を作ればいいなんて、あたしはとうてい思いつきそうもありません……」

僕「僕だってそうだよ。平均値の定理を証明するときに、いきなりこんなこと思いつかない。 ロルの定理については本を読んで覚えていただけだよ」

テトラ「覚えてるというのがすごいです」

僕「細かいところまで暗記しているって意味じゃないよ。 こんなふうにして証明するんだなあ……という方針を理解したっていうこと。 ともかくこれで、僕たちが証明すべきことは、平均値の定理からロルの定理に移ったことになるね」

テトラ「ドミノ倒しのように、ロルの定理が平均値の定理を倒してくれるんですね！」

僕「ロルの定理を倒すのは、僕たちだけどね」

テトラ「そうですね……」

ロルの定理

僕「ということで、僕たちの目標はロルの定理を証明すること」

テトラ「ここでもやはり $g(x)$ は何だかわからないんですよね？　連続性と微分可能性と $g(a) = g(b)$ という条件はありますが、 ほかには何もわかっていない関数……何をどうすればいいのか、さっぱりわかりません。 手の付け所がない問題って、いったいどうしたらいいんでしょう」

僕「ポリヤの問いかけには、 《問題の一部分をとくことができるか》や、 《もっと特殊な問題はとくことができるか》 というものがあるね」

テトラ「平均値の定理を証明する代わりにロルの定理を証明するのは、もっと特殊な問題を解くことですね」

僕「そうだね。ロルの定理でも、関数 $g(x)$ が特殊な場合を考えてみることができるよ。 たとえば関数 $g(x)$ が、 $a \LEQ x \LEQ b$ の範囲で、 $$ g(x) = A $$ という定数関数だったらどうなると思う？　 $A$ は $g(a)$ に等しい定数として」

テトラ「$g(x)$ がずっと $A$ ということですね。それなら $y = g(x)$ のグラフは水平線ですから、 ロルの定理は成り立つと思います。 $a$ と $b$ のあいだのどの点をとっても、接線は水平になりますから。 接線というのも何だか変な感じがしますけれど」

僕「$y = g(x)$ のグラフは $y = A$ という水平線になるから、接線というイメージだと変に感じるかもね。 でも、ともかく $g(x)$ が定数関数だったら、 $g'(c) = 0$ という実数 $c$ は存在するのは確か。 $a < c < b$ を満たすどんな実数 $c$ でも $g'(c) = 0$ になってくれる」

テトラ「でも、それは特殊な $g(x)$ ですから、ロルの定理を証明したことにはなりませんよね？」

僕「ならないね。でも、ここから僕たちは、 $$ g(x) \neq A $$ を満たす $x$ が $a < x < b$ に存在するときの関数 $g(x)$ に限って考えればいいわけだ」

テトラ「それは、 $y = g(x)$ のグラフでいうと、上に出たり下に出たりする部分があるというイメージでいいですよね。 水平線じゃないグラフ」

僕「うん、それでいいよ」

テトラ「ちょっとお待ちください。 たとえば $y = g(x)$ のグラフはこのような形になって、 見つけたいのは、 $g'(c) = 0$ となる $c$ ですよね。接線が水平になるときの接点の $x$ 座標」

僕「そうだね。たとえば」

テトラ「だったら、 $g(c)$ というのは $y = g(x)$ の最大値ということじゃないでしょうか！　だって最大値を取るところでは、 接線は水平になりますから！」

僕「すごい！　それは、ほとんど正解。ただ、注意点が一つあるんだ」

テトラ「注意点……と、いいますと？」