![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。好奇心旺盛で根気強い《元気少女》。
ある日の放課後、僕が図書室に行くと、テトラちゃんが《カード》を眺めていた。
僕「テトラちゃん、それは村木先生の《カード》?」
村木先生は数学教師。 僕たちにときどき《カード》をくれる。 そこには数学の問題が書かれていたり、数式が一つ書かれていたり、 クイズのように謎めいた言葉が書かれていたりする。
僕たちはその《カード》をきっかけに自由に考え、話し合う。 気が向いたらレポートにまとめることもある。 そんな活動は授業とは関係がないし、もちろん成績とも関係がない。 村木先生の《カード》に取り組むことは、僕たちの純粋な楽しみなのだ。
テトラ「あっ、先輩。そうですそうです。今日は、こんな《カード》が……」
テトラちゃんがもらった《カード》

僕「ああ、なるほど。これは《いつものあれ》だね?」
テトラ「はい、そうですね。《いつものあれ》です」
僕とテトラちゃんは、タイミングを合わせて声をあげる。せーの……
「「線型性!」」
そして、僕たちは微笑み合う。息はぴったりあっている。
僕「これは、関数 $f$ が線型性(せんけいせい)を持っているときの式だね。 といっても、村木先生は文字については何も書いていないから、 適当に言葉を補って書いてみようか。こうかな」
$f$ は、定義域と終域のどちらも実数全体の集合である関数とする。
そして、この関数 $f$ は、 任意の実数 $a,v,v_1,v_2$ に対して、 以下の二つの等式を満たすものとする。
$$ \left\{\begin{array}{llll} f(v_1 + v_2) &= f(v_1) + f(v_2) \\ f(av) &= af(v) \\ \end{array}\right. $$
このとき、関数 $f$ は線型性を持つという。
僕「といっても、もちろん、 定義域や終域を実数に限る必要は何もないんだけど」
テトラ「はい、わかります」
僕「線型性のキャッチフレーズは、 《和のナントカは、ナントカの和》 になるよね」
テトラ「はい、そうですね。 $v_1 + v_2$ という和を関数 $f$ に与えると、 $f(v_1) + f(v_2)$ という和になるということですね」
僕「そうそう」
テトラ「もうひとつは、 《定数倍のナントカは、ナントカの定数倍》で、 それは、 $av$ のように、 $a$ 倍した $v$ を関数 $f$ に与えると、 $a$ 倍した $f(v)$ に等しくなる……と」
僕「その通り!」
テトラ「このパターンの式は何度も見たことがありますので、 もう《お友達》です。といっても、あたしは、 $$ f(ax + by) = af(x) + bf(y) $$ という一つの式で覚えていますけど」
僕「そうだね。それで表現することもよくある」
テトラ「線型性が、いろんなところに出てくるということも知ってます!」
僕「うん、そうだね」
テトラ「あたし、最初は不思議でした。 どうして線型性のことをいつも気にするのかというところが気になったんです。 でも、先輩から教えていただいて納得でした」
僕「何だっけ?」
テトラ「たとえば、《和の積分は、積分の和》です。 《和》の形になった関数を積分するとき『和の形になっている』ということを見抜ければ、 和をばらばらにほぐして、 それぞれを積分してから和を求めればいいということがわかるからです。 《式の形》を見抜くことができれば、 やさしくて基本的なものに分けて考えることができるんです」
和の積分は、積分の和
$$ \underbrace{\int \bigl(\, \overbrace{f(x) + g(x)}^{\textrm{和}} \,\bigr) \,dx}_{\textrm{積分}} = \underbrace{ \overbrace{\int\!f(x) \,dx}^{\textrm{積分}} + \overbrace{\int\!g(x) \,dx}^{\textrm{積分}} }_{\textrm{和}} $$
僕「ああ、そういう話をしたことあったね(『数学ガールの秘密ノート/積分を見つめて』参照)」
テトラ「はい、それで《線型性》というものを考える理由がよくわかったんです。 複雑なものを簡単なものに分けて考える。個別撃破に納得です!」
僕「個別撃破……そういえば、 線型性についてリサちゃんが《演算装置の交換》と表現してたよ。 それもまた線型性を考える意味といえるかもね」
テトラ「すみません。 《演算装置の交換》ってどういうことでしたでしょうか。 交換法則のこと……?」
僕「交換法則とは違うけど……ええと、あれは確か、 行列を使った一次変換のときだと思うよ。 座標平面上の点を、行列を使って移動させる話だね。 行列にベクトルを掛けるという計算が線型性を持つ」
テトラ「……」
僕「ほらほら、式で書くとこういう話」
行列による一次変換の線型性

テトラ「ははあ……そういえば、そういうものもありましたね」
僕「そのときに、リサちゃんがこんな図を描いてたよ」
行列による一次変換の線型性を演算装置の交換で表現
《和》
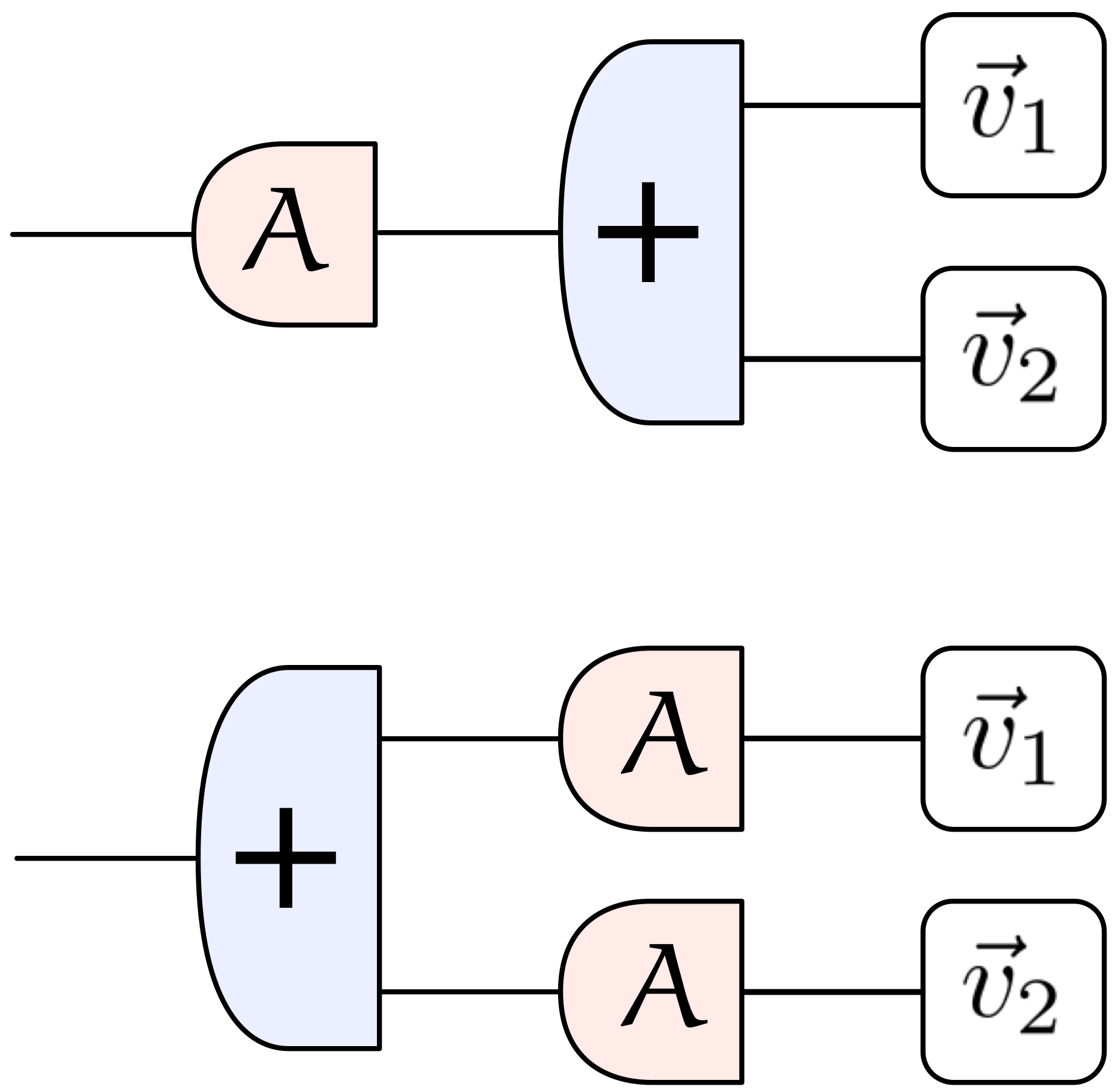
《定数倍》

テトラ「……これは、何と何を交換していることになるんでしょうか?」
僕「そうだね。図をよく見て考えればわかるけど、 たとえば《和》の方の図では、《ベクトルの和を取ってから行列で一次変換したベクトルは、 行列でそれぞれ一次変換してから和を取っても同じだよ》といってるわけだね」
テトラ「《和をとる》という計算と、《一次変換する》という計算の二つを交換している……?」
僕「うん、そういうこと。 それから、《定数倍》の方の図では、《定数倍する》と《一次変換する》の二つを交換している。 交換して何が起きるかという話じゃなくて、 《一次変換する》という演算は、そのように《和》や《定数倍》と交換できる性質を持っているんだよという話」
テトラ「なるほど……線型性というのは、 二つの計算を入れ換えられることだと?」
僕「そうそう、そういうふうに見なすことができるという意味だね。おもしろい」
テトラ「おもしろいですけれど……ちょっと頭がぐるぐるしてきました! ところで、言葉の使い方で質問があります」
僕「言葉の使い方?」
テトラ「あのですね、似ているような違うような言葉がたくさん出てきます。 関数、写像、計算、演算、それから変換……これって同じものなんでしょうか?」
僕「ああ、なるほど。確かに似てるよね。 《関数》の定義はいいよね。 《写像》は関数を少し一般化している。 《関数》は、定義域や終域が数の集合のことが多いけど、 《写像》は、数の集合でなくても使うよ」
テトラ「はい。その二つは大丈夫です」
僕「それから、《計算》や《演算》はもっと具体的なニュアンスが強いかも。 《計算》や《演算》は数を使って別の数を作ることになるかなあ……いや、 でも、真偽値を扱う場合も《計算》や《演算》と呼ぶし、 数に限った話でもないし……しっかりした定義は僕にはできないな」
テトラ「《関数》や《写像》の方は《対応そのもの》に注目していますが、 《計算》や《演算》は、そのような対応を実際にどうやって作り出すかに注目しているように感じます」
僕「確かにそういうニュアンスはありそうなんだけど、 たとえば、 $+$ や $=$ や $<$ のような記号のことを《演算子》というけど、 それは必ずしもどうやってその計算を行うかまで注目しているわけじゃないよね」
テトラ「なるほどです。 関数は英語だとfunctionですよね。写像はmappingで、演算子はなんでしょう」
僕「operatorだね」
テトラ「operator……操作するもの……?」
僕「《関数》や《写像》という言い方だと、対応させるだけだからいいけど、 《計算》って難しいね。 たとえば円周率 $\pi$ を自然対数の底 $e$ 倍した数 $\pi e$ は実数になるけど、 これは《計算》っていえるのかな。 $\pi$ も $e$ も、 十進法で表したら無限に続く数字が続いてしまう……」
テトラ「難しいですね」
テトラ「ところで、先ほど先輩は、 行列による一次変換には線型性があるというお話をなさいました」
僕「そうだね」
テトラ「あたしは、なるほど! と一瞬思ってしまったんですが、 確認させていただいてもいいですか?」
僕「確認というと?」
テトラ「あのですね、 実際に書いてみるということです」
僕「実際に……ああ、成分を使って表すということ?」
テトラ「そうです、そうです。 《成分を使って表す》といえばよかったんですね。 たとえば、行列 $A$ を、 $$ A = \left(\begin{array}{cc} p & q \\ r & s \end{array} \right) $$ だとすると、一次変換の線型性というのはこういうことですよね?」
行列による一次変換の線型性
《和の一次変換は、一次変換の和》
$$ \begin{align*} \left(\begin{array}{cc} p & q \\ r & s \end{array} \right)\left\{\VECV{x_1}{y_1} + \VECV{x_2}{y_2}\right\} &= \left(\begin{array}{cc} p & q \\ r & s \end{array} \right)\VECV{x_1}{y_1} + \left(\begin{array}{cc} p & q \\ r & s \end{array} \right)\VECV{x_2}{y_2} \\ \end{align*} $$
《定数倍の一次変換は、一次変換の定数倍》
$$ \begin{align*} \left(\begin{array}{cc} p & q \\ r & s \end{array} \right)\left\{a\VECV{x}{y}\right\} &= a \left(\begin{array}{cc} p & q \\ r & s \end{array} \right)\VECV{x}{y} \\ \end{align*} $$
僕「そうそう、その通りだね。 そして、テトラちゃんのことだからこれを具体的に計算して確かめる……」
テトラ「あ、いえいえ。それは以前何度か書いて確かめたので、 もう納得しているんです」
僕「そうなんだ」
テトラ「実はあたし、 先ほど《似て非なるもの》について思いついたんですよ」
僕「似て非なるものって?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2017年9月15日)