第168回 シーズン17 エピソード8

組み立てペンタゴン（後編）

放課後の図書室

テトラ「先輩！　先日は正 $5$ 角形、楽しかったですねっ！」

僕「そうだね」

テトラ「実はですね、あれからいろんなことが気になって、 家で計算していたんですよ。テトラの話、聞いていただけますか？」

僕「もちろん、いいよ。どんな計算？」

テトラ「単位円に内接する正 $5$ 角形の頂点を考えるとき、 先輩は単位円の円周上にある点を $(\cos\theta,\sin\theta)$ と置きました」

僕「そうだね。それはすごく自然なことだと思うけど。 $\cos$ と $\sin$ の定義から」

テトラ「はい。あたしはそこからすぐに、 頂点に対応する $5$ 個の角度が $\frac{2\pi}{5}$ ずつ増えていることがわかりましたし。 だってひとまわり $2\pi$ を $5$ 等分するんですから。ですよね」

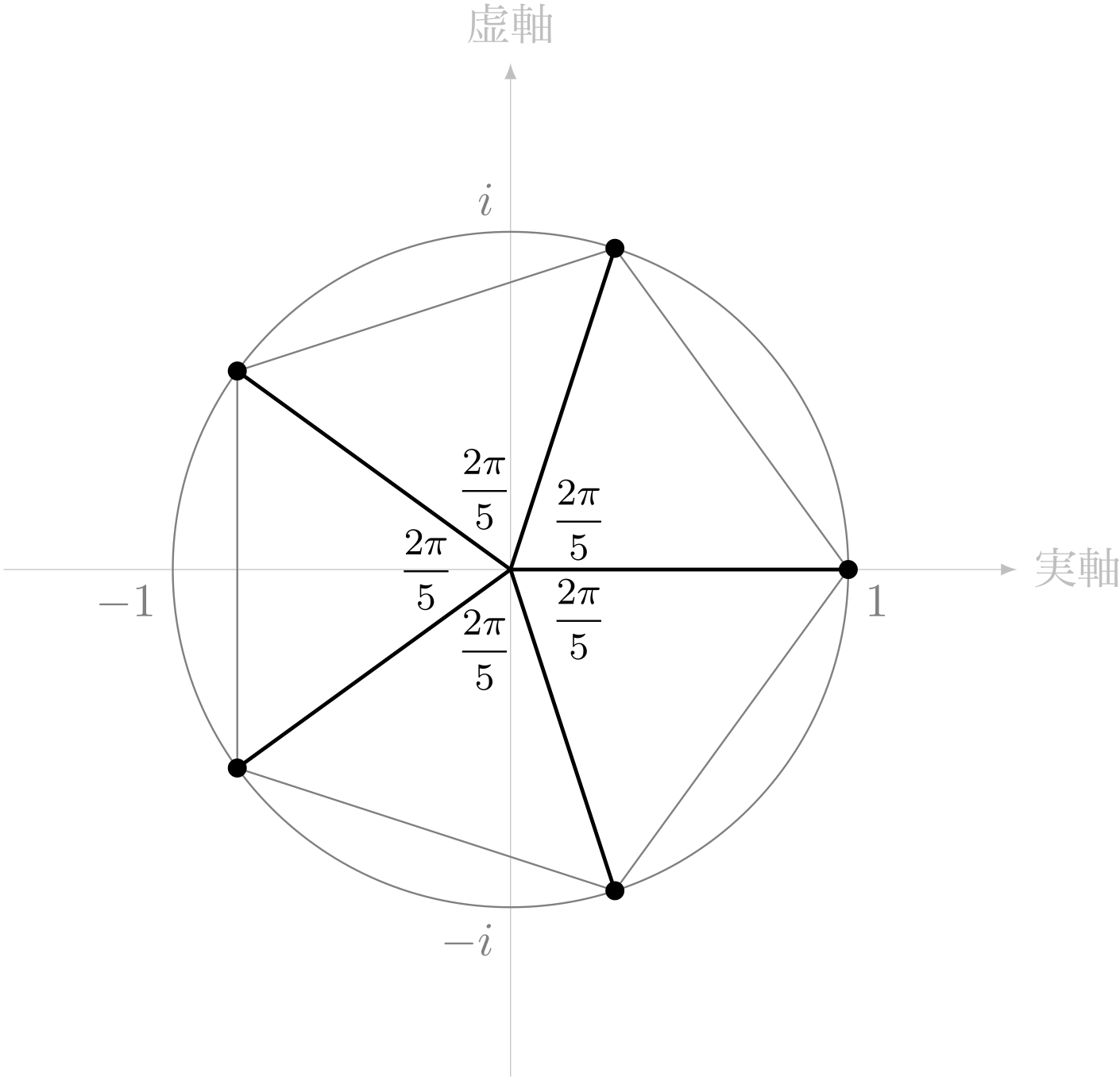
僕「うん。偏角だよね。複素数は一般に $r(\cos\theta + i\sin\theta)$ と表せるけど、このときの $\theta$ が偏角。 単位円の円周上なら、 $r = 1$ だけどね……で、そこから何か計算したの？」

テトラ「はい。先輩が話してくださった《正 $5$ 角形の頂点と $z^5 = 1$ の関係》のことをずっと考えていたんです。 この正 $5$ 角形の頂点を想像しながら……そこであたし、気付きました。 複素平面で頂点に対応している複素数が $z^5 = 1$ の解ということは、 $\cos\frac{2\pi}{5}+i\sin\frac{2\pi}{5}$ を $5$ 乗したら $1$ になるということですよね？」

僕「え？　ああ、もちろん、その通りだよ。その話、しなかったっけ」

テトラ「すみません、違うんです。そのお話は聞いていました。 でも、あたしの中ではどうも納得していなかったようなんです。 家で、 $\zeta_0,\zeta_1,\zeta_2,\zeta_3,\zeta_4$ のことを考えていたら……」

僕「うん」

テトラ「……そうしたら《$5$ 乗したら $1$ に等しくなる $5$ 個の式》がぱああっ！と浮かんで来て、はわわっ！となって……」

僕「なるほど」

テトラ「それから、この $5$ 個の式も、確かにこれが成り立つ……とわかったんです」

僕「ああ、それは《腑に落ちた》ってやつだね！　その気持ち、 よくわかるよ。前から見たことがある式のはずなのに『そういうことだったんだ！』 って突然気付くこと、あるから」

テトラ「あ、先輩もそうなんですか？」

僕「すごく基本的なところでは、 数式の《因数分解》と《展開》が逆の計算なんだ！と気付いたときとかね」

$$ \begin{array}{rcl} a^2 + 2ab + b^2 &\stackrel{\REMTEXT{因数分解}}{\longrightarrow}& (a+b)^2 \\ &\updownarrow& \\ a^2 + 2ab + b^2 &\stackrel{\REMTEXT{展開}}{\longleftarrow}& (a+b)^2 \\ \end{array} $$

テトラ「なるほど」

僕「それから $2$ 次方程式の《解と係数の関係》をはじめて習ったときもね。 《解と係数の関係》って、意味がぜんぜんわからなかったのを覚えてるよ。 式の変形は追えるんだけど意味がわからない。 でも、《解の公式》と《解と係数の関係》が似ていることをやってるって、気付いたときは感動したなあ」

• 《解の公式》は、係数で《解》を表す。
• 《解と係数の関係》は、係数で《解の和と積》を表す。

テトラ「な、なるほど……」

僕「さっきのテトラちゃんの $5$ 個の式はもちろん正しいけど、 $\theta = \frac{2\pi}{5}$ と置くとこうなるね」

テトラ「ああ、そうですね」

僕「ド・モアブルの公式を使って書き直すとこうなるかな」

僕「そして、ここまでくればあたりまえ。だって、 $\theta = \frac{2\pi}{5}$ を $5$ 倍したら $2\pi$ になる。 $2\pi$ の整数倍だと $\cos$ は $1$ で、 $\sin$ は $0$ になるから、こうなるよね}

テトラ「あ、はい……そ、それでですね。あの……あたしが考えていたことに戻るんですが」

僕「あ、そうだ。ごめんごめん。テトラ先生が話していたんだった。どうぞどうぞ」

テトラ「単位円に内接する正 $5$ 角形の頂点 $\zeta_0,\zeta_1,\zeta_2,\zeta_3,\zeta_4$ は どれも $5$ 乗すると $1$ になるんですから、 $5$ 回分ジャンプすると、ぜんぶ $1$ にたどり着くんですよ！　 たとえば、 $\zeta_1$ の場合は、反時計回りにぐるっと回って $1$ にたどり着きます」

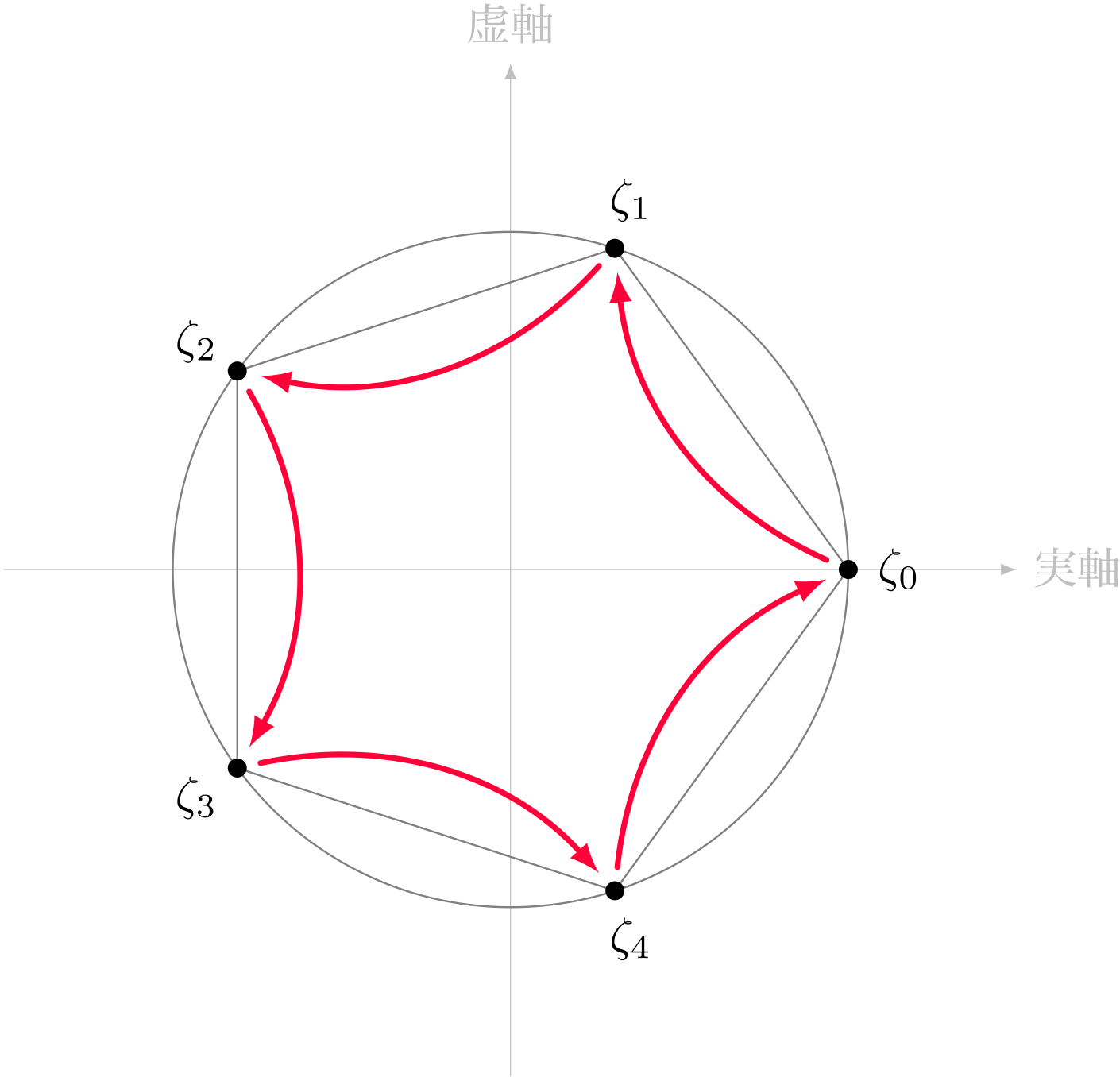
僕「なるほどね。ええと、 $\zeta_1$ を $5$ 回分ジャンプするというのは、 $\zeta_1^1,\zeta_1^2,\zeta_1^3,\zeta_1^4,\zeta_1^5$ を複素平面でたどるという意味かな。 ちゃんというと、 $\zeta_0 = 1$ から始めて、 $\zeta_1$ を繰り返し掛けていくと…… $$ \begin{align*} \zeta_0\zeta_1 &= \zeta_1 \\ \zeta_1\zeta_1 &= \zeta_2 \\ \zeta_2\zeta_1 &= \zeta_3 \\ \zeta_3\zeta_1 &= \zeta_4 \\ \zeta_4\zeta_1 &= \zeta_0 \\ \end{align*} $$ ……のようになるということだよね」

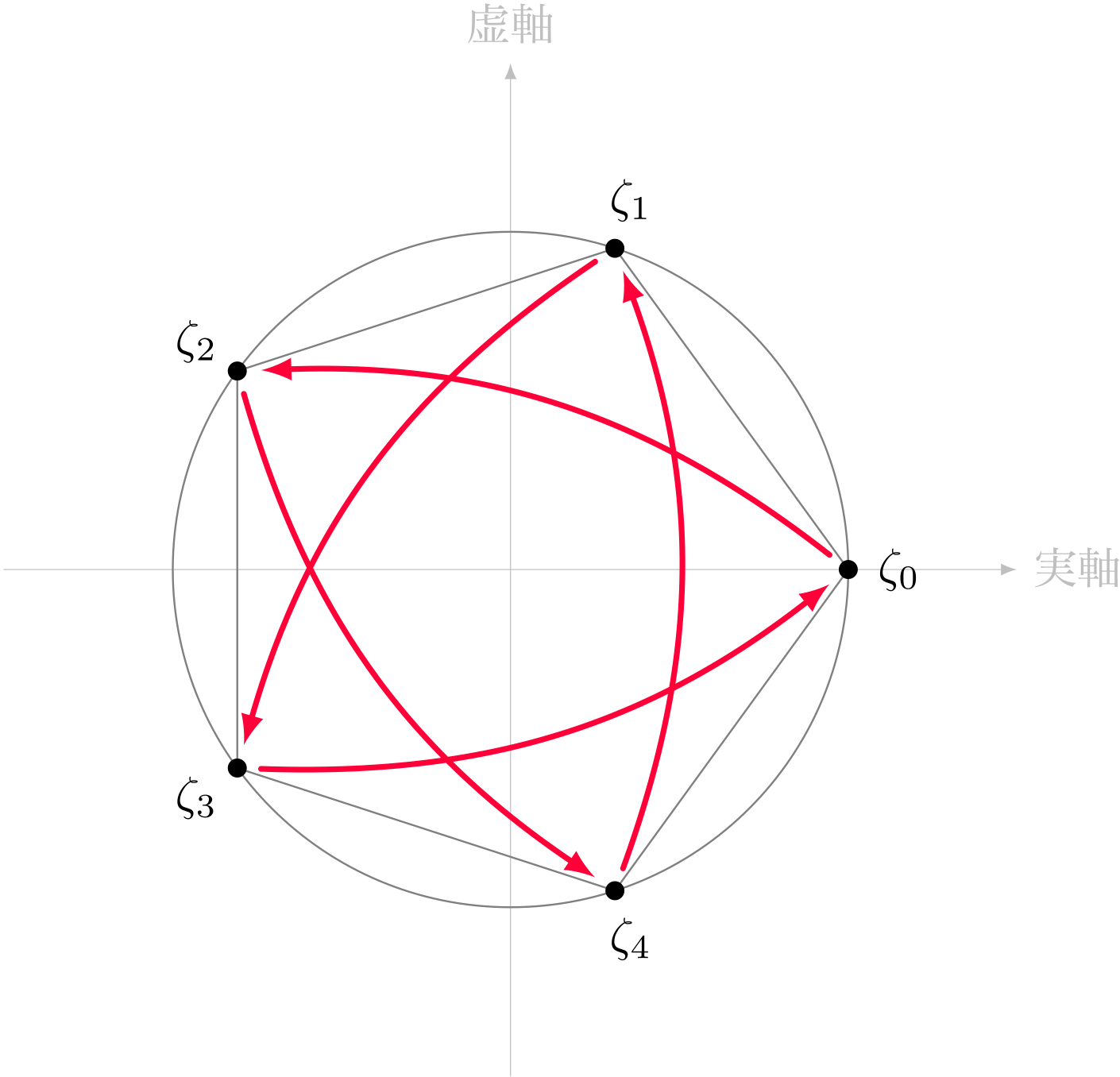
テトラ「はい。そして、 $\zeta_2$ も同じように $5$ 回ジャンプで $1$ に着きます」

$$ \begin{align*} \zeta_0\zeta_2 &= \zeta_2 \\ \zeta_2\zeta_2 &= \zeta_4 \\ \zeta_4\zeta_2 &= \zeta_1 \\ \zeta_1\zeta_2 &= \zeta_3 \\ \zeta_3\zeta_2 &= \zeta_0 \\ \end{align*} $$

僕「……」

テトラ「$\zeta_3$ も同じように $5$ 回ジャンプで $1$ に着くんですが、これは $\zeta_2$ の逆回りで……」