第165回 シーズン17 エピソード5

水面に映る星の影（前編）

図書室にて

テトラ「さて、これは……」

僕「テトラちゃん、何を考えているの？　それは村木先生の《カード》？」

テトラ「あ、先輩！　はい、そうです。村木先生からいただいたんですが、 これ、何も書いていないんですよ」

僕「正 $5$ 角形だ」

テトラ「正 $5$ 角形です」

僕「何も書いてない」

テトラ「何も書いてないです」

僕「今度は正 $5$ 角形の天使？」

テトラ「え？」

僕「いやいや、こっちの話（第139回参照）」

テトラ「正 $5$ 角形について考えよ、ということでしょうか。 この形を使って何かおもしろいことを……」

僕「まあ、もともと、 村木先生が僕たちにくれる《カード》は問題になってないこともよくあるからね。 図形といえば、先日ユーリに複素平面の話をしたなあ」

テトラ「複素平面！　ユーリちゃんはいつもすごいですね。 何でもできちゃいます」

僕「複素数とベクトルの話をしたんだよ。 $a+bi$ という複素数を座標平面上の点 $(a,b)$ だと思えば、 複素数を使って図形を描けるよね。 《図形》を《点の集合》だと見なして」

テトラ「はい、そうですね」

僕「といっても簡単な話だけしかできなかったけどね。 たとえば共役複素数（きょうやくふくそすう）の話はしなかったし」

テトラ「共役複素数……といえば《水面に映る星の影》ですね！」

僕「みなもにうつるほしのかげ？」

テトラ「はい、そうです。 $$ a+bi $$ と $$ a-bi $$ のことですよね、共役複素数って」

僕「そうだね。 複素数 $a+bi$ の共役複素数は $a-bi$ だし、 複素数 $a-bi$ の共役複素数は $a+bi$ になるね。 $a+bi$ と $a-bi$ は複素共役（ふくそきょうやく）であるという言い方もするよ」

• 複素数 $a+bi$ の共役複素数は、 $a-bi$ である。
• 複素数 $a-bi$ の共役複素数は、 $a+bi$ である。
• $a+bi$ と $a-bi$ は複素共役である。

テトラ「はい、その $2$ つの複素数……つまり、 $a+bi$ と $a-bi$ を複素平面に描くと $2$ 個の点になりますよね。 それがちょうど、実軸を水平線として《水面に映る星の影》みたいだなあ、 と思ったんですよ（『数学ガール／ガロア理論』参照）」

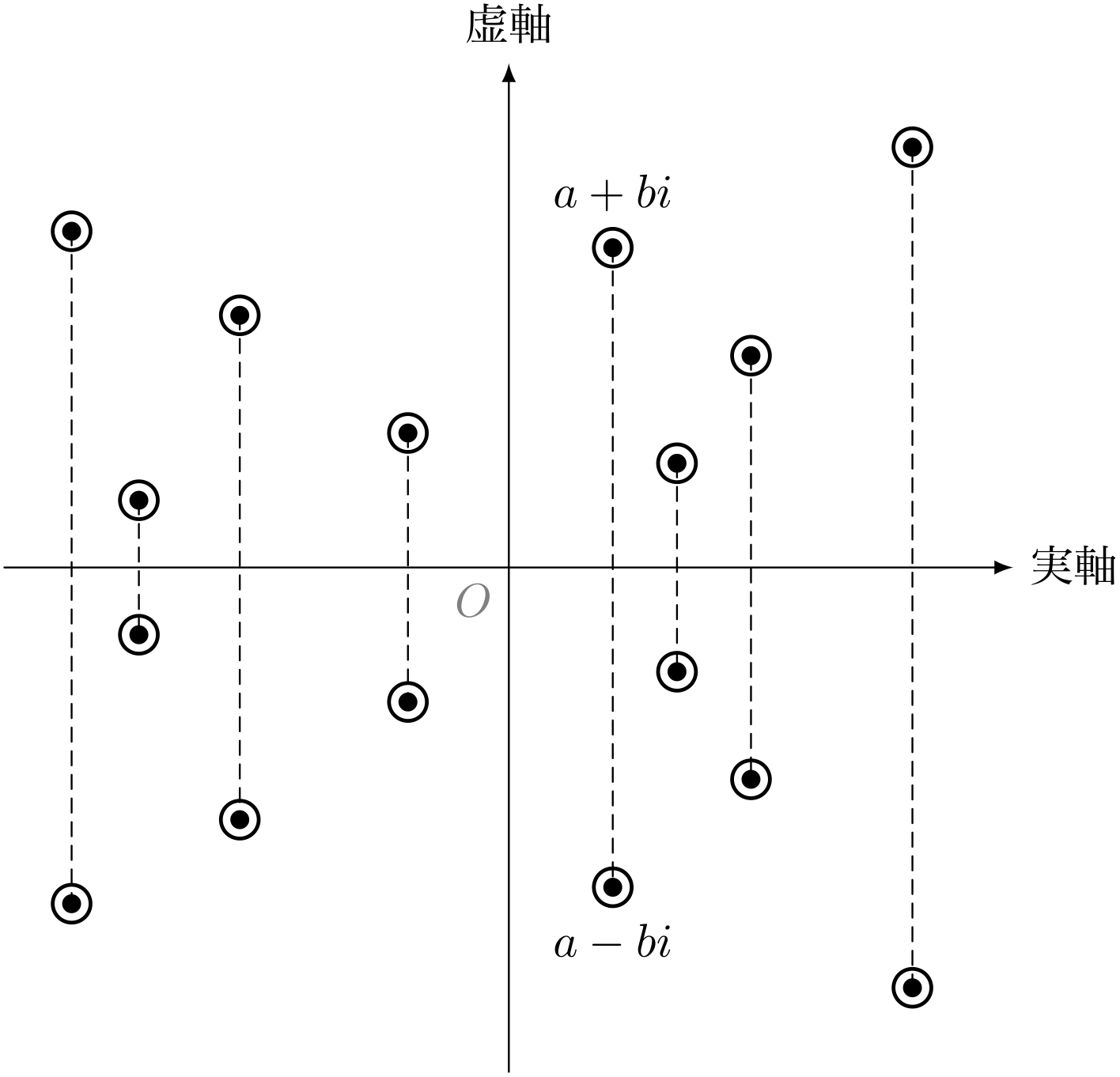
僕「ああ、確かに。 実軸を対称軸として、 $a+bi$ と $a-bi$ が対称の位置にあるからだね」

テトラ「共役複素数って、よくでてきますよね」

僕「うん。 $2$ 次方程式の解の公式にも出てくる」

テトラ「なるほど、そうですね。 $A + Bi$ の共役複素数は $A - Bi$ と……」

僕「そうそう。共役複素数はとてもおもしろくて、足しても掛けても必ず実数になるよね」

テトラ「ええと？　これはあたしでも確かめられそうです。 計算すればいいんですよね？」

$$ \begin{align*} (a+bi) + (a-bi) &= a + bi + a - bi \\ & = 2a \\ (a+bi)(a-bi) &= aa - abi + bia - bbii \\ &= a^2 - abi + abi - b^2i^2 \\ &= a^2 - (-b^2) \\ &= a^2 + b^2 \\ \end{align*} $$

僕「そうだね。和は $2a$ になって、積は $a^2+b^2$ になる。だから……」

テトラ「はい、だから、 $2a$ も $a^2+b^2$ も実数なので、和も積も実数になっていることが確かめられました」

僕「そういうこと。特に積がおもしろいんだよ！」

テトラ「積というと $(a+bi)(a-bi)=a^2+b^2$ ですが？」

僕「それだよ。だってほら、複素数の絶対値の二乗に等しくなってる」

$$ (a+bi)(a-bi) = a^2 + b^2 = \sqrt{a^2+b^2}^2 = \ABS{a+bi}^2 $$ $$ (a+bi)(a-bi) = a^2 + b^2 = \sqrt{a^2+b^2}^2 = \ABS{a-bi}^2 $$

テトラ「ははあ……確かにそうですが」

僕「納得いかない？」

テトラ「いえいえ！　そんなことはありません」

僕「ただ？」

テトラ「ただ……あの、すみません。いつもあたしは《でも、 これは何なんだろう》って思ってしまうんです」

僕「そうだね。テトラちゃんがよくいう、So what? （だから何？）かな」

テトラ「それです！　先輩がいろんな式を次々に見せてくださったり、 こんな関係もあるよと教えてくださいます。 それはおもしろいですし、なるほど！と思うこともよくあるんですが、 胸の中に《もやもや》が残るんです。『この式は何なんでしょうか』や 『そういう関係が導けるから何？』……という《もやもや》です」

僕「うん、よくわかるよ。 テトラちゃんとはよく話してる長い付き合いだし。 よくそういうこと、あるよね」

テトラ「す、すみません。何だか素直じゃなくて」

僕「そんなことないよ。言われたことをそのまま鵜呑みにするだけが素直じゃないし。 それにね、テトラちゃんは自分の《わかってない気持ち》に対して、いつも素直なんだよ」

テトラ「あっ、そういっていただけると……ありがとうございます」

僕「ところで共役複素数の話なんだけど、 『積も和も実数になる』とか『積が絶対値の $2$ 乗になる』とかいうことは……それだけじゃ《だから何？》に答えられないかも。 僕は数式をいじるのが好きなんだけど、それはそれ自体が楽しいからだし」

テトラ「そうなんですね。あたしはそういう境地にはなれそうにないです」

僕「あっ、でもね。別に数式をいじってるだけがすべてでもないんだよ。 計算しているとね、ときどき何かに《つながる》ことがあるんだ。 授業のときや、テスト中でも『あれ、前に似たような計算をしたことがあったぞ』って思うんだ。 ふだんから、自分で手を動かして計算していると、気付くことがたくさんあるんだよ」

テトラ「そうなんですね」

僕「そうだよ。そうそう、数式とも長い付き合いだと、 だんだん《こういうこと、よくあるなあ》というのが集まってくるんだね、経験として。 テトラちゃんもよく言うよね。概念と《お友達になる》って。 数式を使って計算しているというのは、 友達とのおしゃべりと似ているかも。 友達と話すとき、いちいち『いまの話は何の役に立つか！どんな意味を持つか！』なんて考えないよね」

テトラ「それは……そうですね。 でも、お話が終わった後になってから、 《あのときの、あの人の、あの言葉は、どういう意味を持っていたの？》 と思うことは……ええと……よくあります」

僕「うん。それは数式をいじっているときと同じだ！」

テトラ「なるほど……なるほどです、はい」

特殊な値

僕「テトラちゃんは『文字がたくさん出てくるとパニックになる』ってよく言うよね」

テトラ「あ、そうですね。《あわあわ》しちゃいます。 で、でも、最近はかなり持ちこたえていますよ……」

僕「うん、それでね。数式で遊ぶときには《文字の導入による一般化》をして、一般的に考えることもあるけれど、逆もあるんだ。 《変数への代入による特殊化》で楽しむことがあるよ」

テトラ「はあ……」

僕「たとえばさっきの複素数の積 $(a+bi)(a-bi) = a^2 + b^2$ というのは ごちゃごちゃした式に見えるかもしれないけど、 ここで特殊な場合を考えてみる。僕が好きなのは単位円だね。 つまり、 $$ a^2 + b^2 = 1 $$ を満たすような状況を考える。これは、 $$ \ABS{a+bi} = 1 $$ そして、 $$ \ABS{a-bi} = 1 $$ という状況のこと」

テトラ「単位円というと半径が $1$ の？」

僕「そうそう。複素平面でいうと、原点を中心に、 半径を $1$ にした単位円。その円周上の点が $a^2 + b^2 = 1$ を満たしてる」

テトラ「これが……特殊化になるんですか」

僕「そうだよ。 $a,b$ がどんな実数でもかまわないとすると、 $a+bi$ はどんな複素数でも表せる。これは一般的な話。 でも、 $a,b$ は実数だけど、 $a^2 + b^2 = 1$ という条件を満たさなきゃいけないという制約をかける。 このとき $a+bi$ という複素数にも制約がかかるわけだね」

テトラ「はあ……す、すみません。またつい心の中で『So what?』という声が……」

僕「だよね。それで、僕はこんなふうに式変形したくなる。 $a^2 + b^2 = 1$ のとき……」

テトラ「……」

僕「つまり、 $a^2 + b^2 = 1$ という条件があると、 《共役複素数を求める》ことが《逆数を求める》ことと同じだとわかったことになるね！ 僕はこういうのが大好きだな」

テトラ「共役複素数で逆数が求まる？」

僕「そうだね。絶対値が $1$ のとき、 共役複素数で逆数が求まるし、逆数で共役複素数が求まる。 《$a+bi$ から $a-bi$ を求める》というのは、 ふつうに考えると《$bi$ という虚数部分の符号を反転させる》というやりかたになるよね」

テトラ「はい、そうですね」

僕「でも、 $a^2 + b^2 = 1$ という条件があれば、 《$a+bi$ から $a-bi$ を求める》というのは、 《$a+bi$ から逆数の $\frac{1}{a+bi}$ を求める》というのと同じ計算になるんだよ。 だって、 $a-bi = \frac{1}{a+bi}$ なんだからね」

テトラ「ああ、はいはいはい」

僕「《共役複素数》と《逆数》のように、ちょっと見ただけだと関係なさそうなものが、急に関係が見えてくるっていうのは楽しくない？」

テトラ「なるほどです！　少し、おもしろさがわかってきました。 あたしが《共役複素数》というと《水面に映る星の影》 だと感じるのに似ています。違う姿が見えるんですね？」

僕「ああ、そうかも！　そうだ、言葉大好きテトラちゃんだったら、 こういうプレゼントがあると喜ぶかな」

テトラ「プ、プレゼント？　喜びますっ！」