![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/数を作ろう』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだけれど飽きっぽい。
ユーリ「お兄ちゃん。ちょっと、これ見て!」
ユーリはそういって一枚の紙を出した。
ユーリの紙
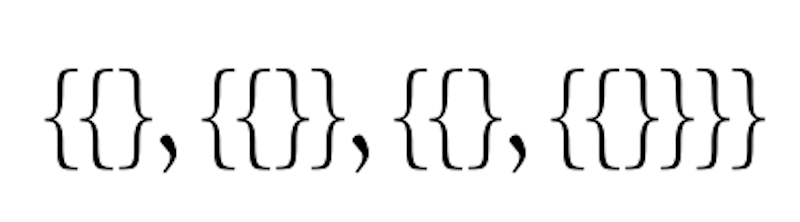
ユーリは僕のいとこ。近所に住んでいる中学生だ。
休みの日になるといつも僕の家に遊びにやってくる。
僕「うん?……ああ、なるほど。知ってる知ってる。これはね」
ユーリ「ちょーっと待ったー!」
僕「え?」
ユーリ「《知ってる知ってる》は、知らない人が言う言葉って、 お兄ちゃんいつも言ってるじゃん! そんなに安直に《知ってる知ってる》なんて言っていいの?」
僕「いや、そんな格言みたいなこと言った覚えはないけど……この数式がどうしたの?」
ユーリの紙
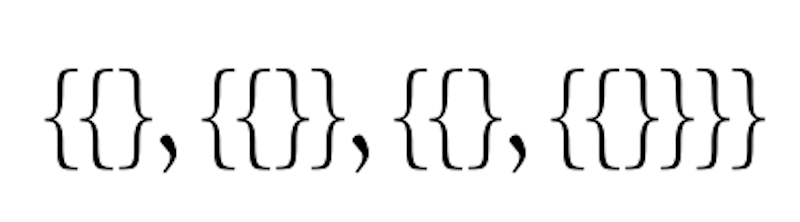
ユーリ「あ、やっぱり数式なんだ。あのね、これはとあるルートから入手した秘密文書なんだよ」
僕「そういうのはいいから。どうせまた、ユーリの《友達》から出されたクイズだろ?」
ユーリには、いつも《数学対決》しているボーイフレンドがいるのだ。
《数学対決》って何だよ……
ユーリ「ま、確かに、クイズみたいな感じだけどさ。ともかく、問題は《この数式は何か》って話。 お兄ちゃんは関心あるかもにゃあ? と思って持ってきたんだよん」
僕「とか何とかいって、こっちに考えさせたいんだろ? ともかく、これは有名な話だよ」
ユーリ「有名な話ってことは、《知ってるかどうかの問題》てゆーこと? 《考えてわかる問題》じゃなくて」
僕「うーん、何も知らないのにこの紙だけ見せられて意味が分かる人というのは、 ほとんどいないと思うよ。いや、どうかな……いずれにしろ、 このままだと読みにくいから、少し書き換えて、読みやすくしてみようか」
ユーリ「そしたら、謎が解ける?」
僕「どうかな」
ユーリ「この数式を書き直すって、どーすんの?」
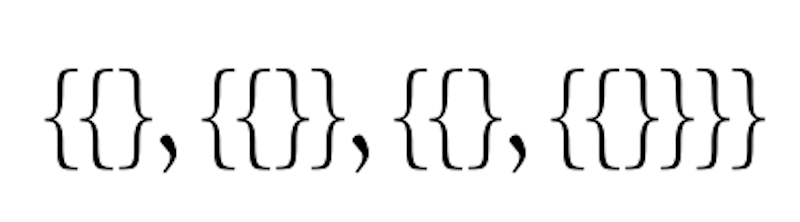
僕「うん、カッコの大きさが全部同じだと、 すごくごちゃごちゃして見える。 だから、こんなふうに大きさを変えてみよう」
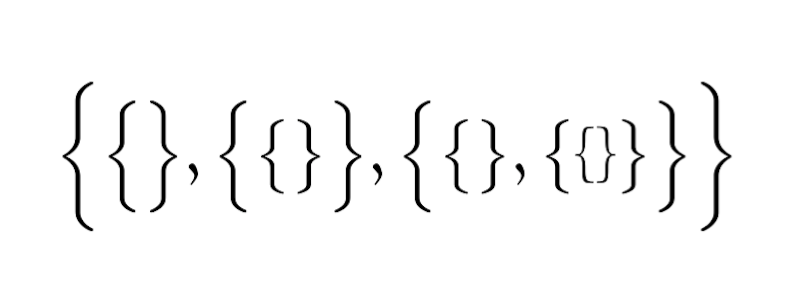
ユーリ「おー なるほど これは とっても みやすくなったなー」
僕「なぜ棒読み」
ユーリ「だって、たいして変わらないもん」
僕「そんなことないよ。よく見てごらん。一番外側の $\{\quad\}$ の中には、 $3$ 個の要素が入っていることがわかるだろ? コンマで区切られて」
$3$ 個の要素
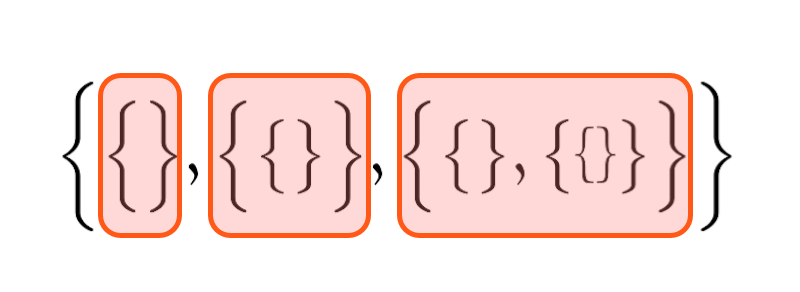
ユーリ「ははーん、うん、これならわかるよ。確かに $3$ 個」
僕「この数式は、 $3$ 個の要素を持っている集合を表しているんだよ。 ユーリは集合のことはもう知ってるよね。 数学的なものをコンマで区切って並べて、 それを $\{ \quad \}$ でくくってひとまとめにして表す」
ユーリ「うん、お兄ちゃん、よく話してくれるよね。集合のこと」
CM
ユーリ「『数学ガールの秘密ノート/場合の数』や、 『数学ガール/ゲーデルの不完全性定理』でも、 ていねいに教えてくれたよね、お兄ちゃん!」
僕「なにこの強引なコマーシャル」
ユーリ「気にしない、気にしない」
僕「ともかく、集合は、数学でとっても大切なものだからね。 ものの集まりを《集合》と呼んで、 集まった個々のもののことを《要素》と呼ぶ」
ユーリ「覚えてるよん。偶数の集合は $\{ 0, 2, 4, 6, \ldots \}$ とか」
僕「そうそう。それは《$0$ 以上の偶数全体の集合》といえるね。 $0$ や $2$ などはその集合の《要素》になる。 それと同じように考えると、ユーリの持ってきた数式は、 $1$ 個の集合を表していて、その集合には $3$ 個の要素が属しているといえる」

ユーリ「そーだけど……これって、要素も集合で、集合が要素? あれ?」
僕「うんうん、そこがややこしいところだよね」
$3$ 個の要素はそれぞれがまた集合になっている
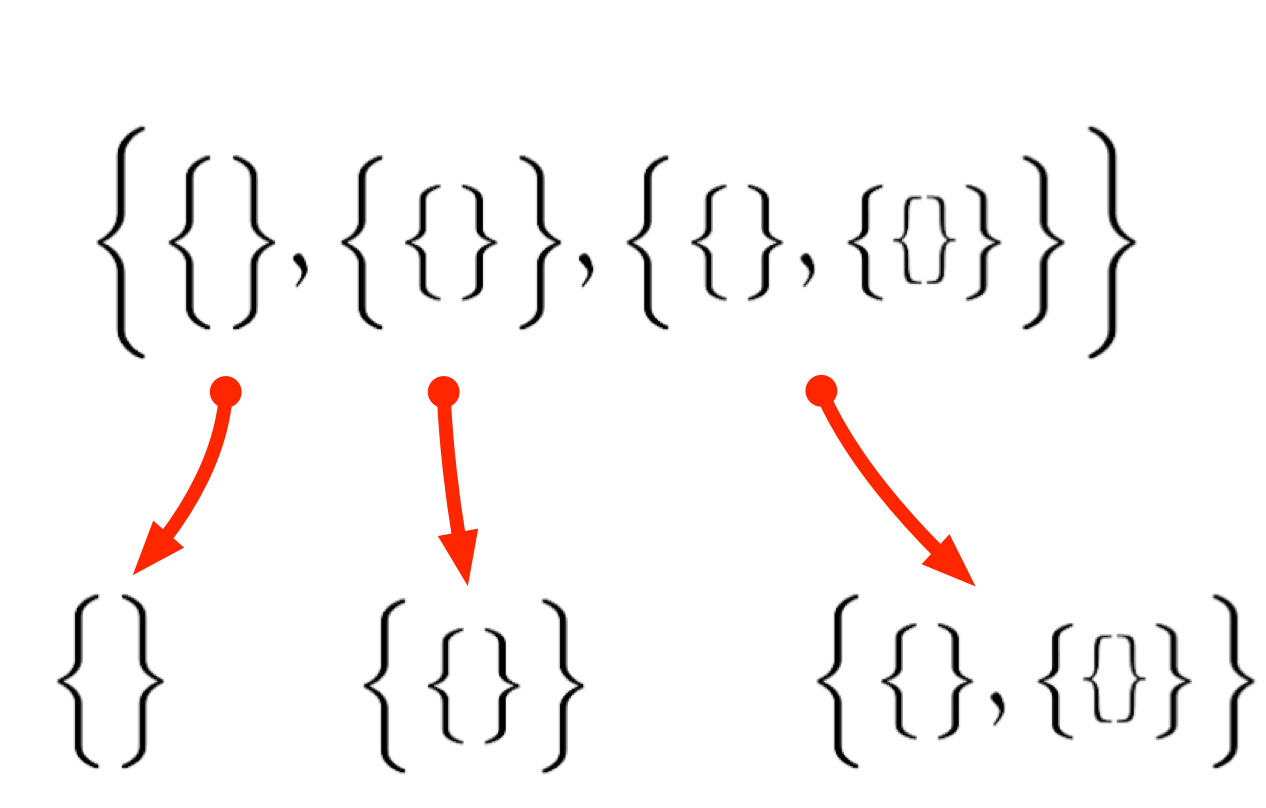
ユーリ「ふんふん。にゃるほど?」
僕「それで、この数式の意味なんだけど」
ユーリ「そんなことより、お兄ちゃん。ユーリ思ったんだけど、 いまバラバラにした $3$ 個の要素って、それぞれがまた集合なんでしょ?」
僕「そうだよ」
ユーリ「でね、もしかして、それぞれの集合の要素もまた集合になってない?」
僕「そうだね!」
ユーリ「こんな感じでもっとバラバラにできる!」
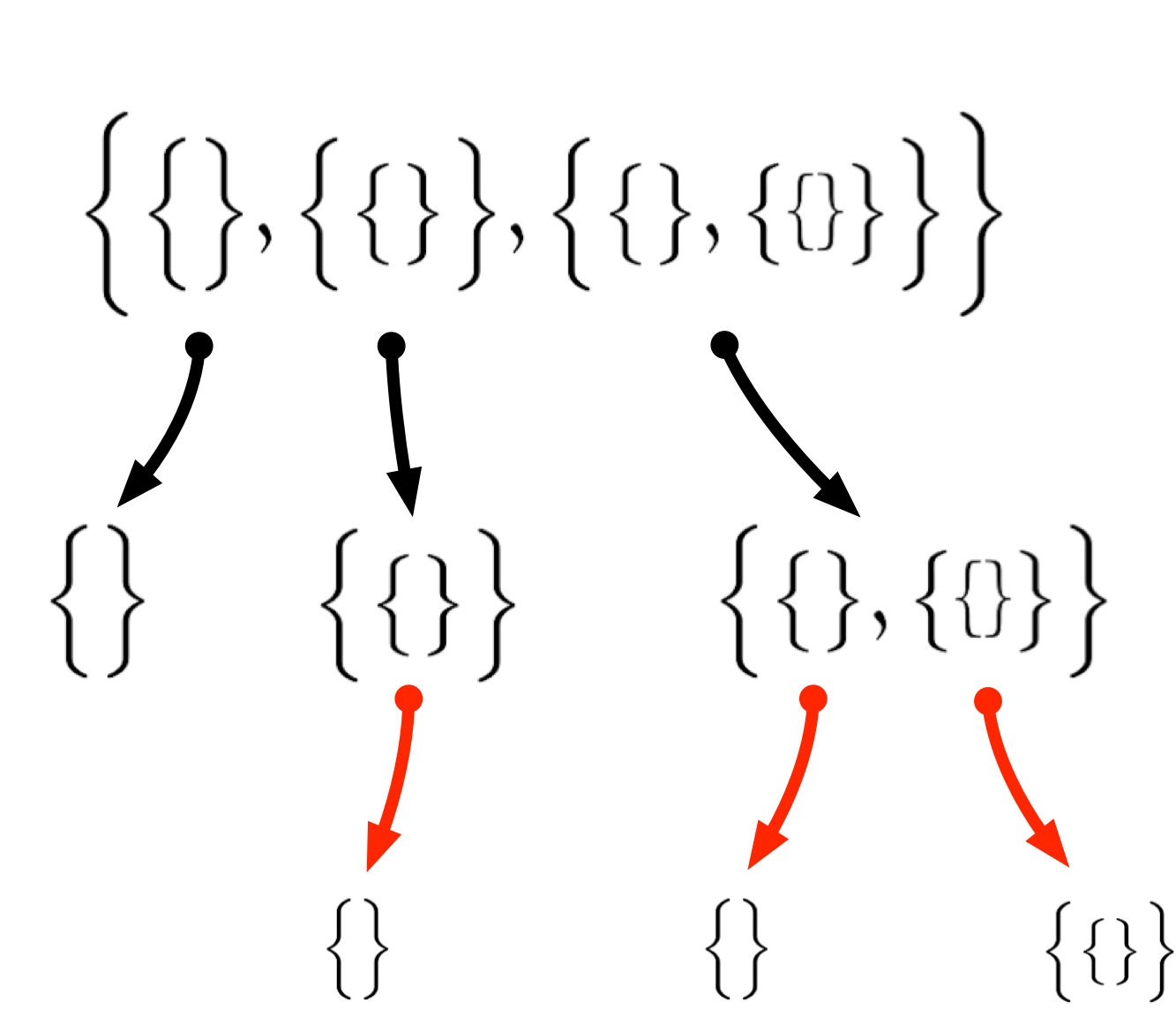
僕「おお、いいねえ……」
ユーリ「あ! もっかいバラバラにできるよ!」
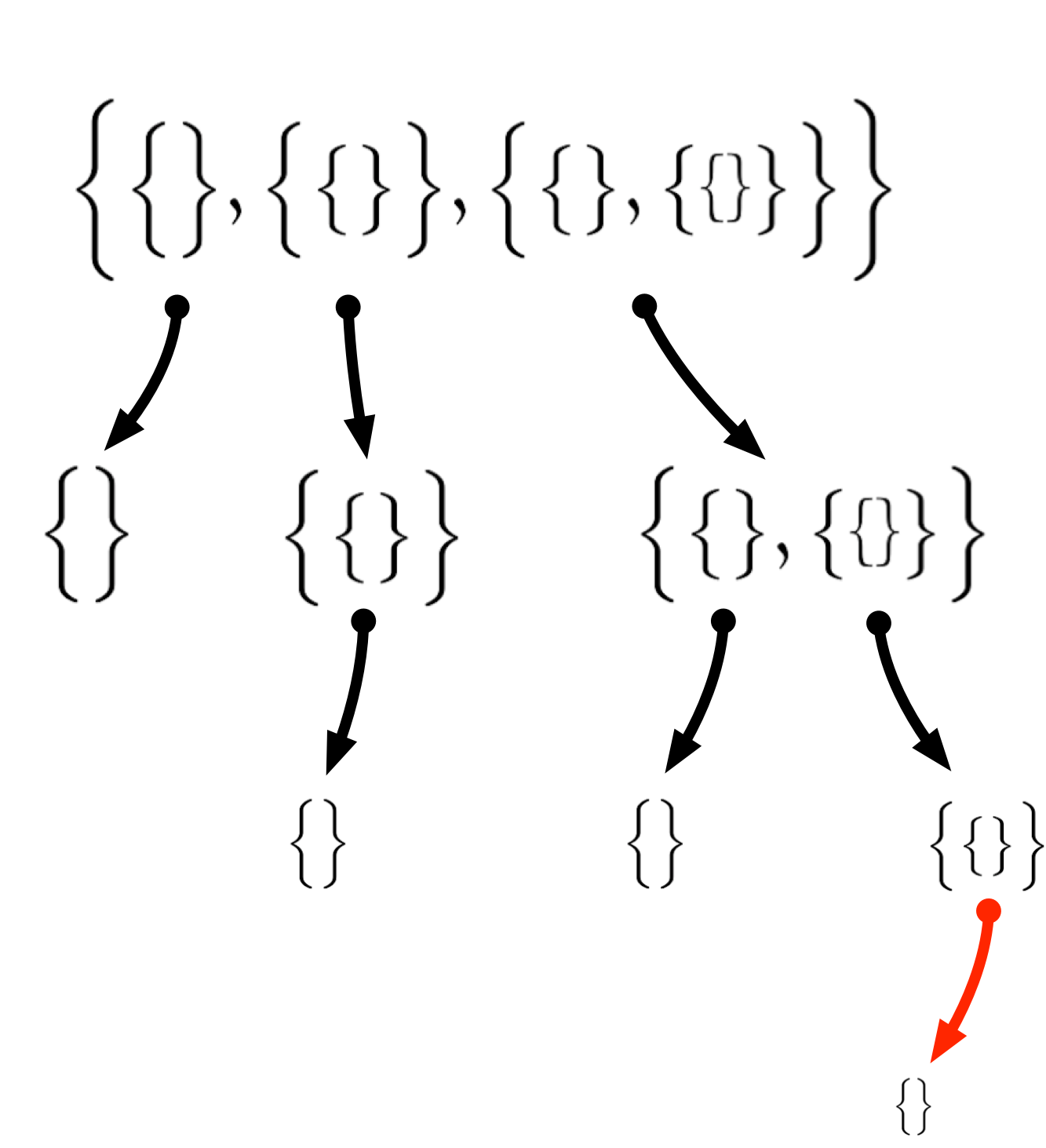
僕「そうだね。ユーリの発見はすごいな!」
ユーリ「あー……でも、これ以上はバラバラにできにゃい。要素、もう、なくなっちゃったから」
僕「うん。 $\{\,\}$ は要素が $1$ 個もない集合を表しているからね。空集合(くうしゅうごう)だ」
ユーリ「くうしゅうごう……これもお兄ちゃんよく話してくれるね」
僕「うん、じゃあ、話を戻して、この数式の意味を考えてみよう」
この数式の意味?
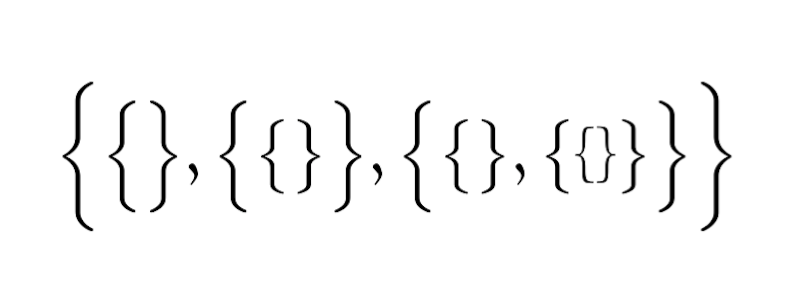
ユーリ「数式の意味って?」
僕「この数式は、そもそも何を表しているんだろうか、ってこと。ユーリはどう思う?」
ユーリ「何を表しているかって……空集合を集めて、集合を作ったものじゃないの?」
僕「実はね、ユーリが持ってきたこの数式は《空集合からスタートして、数を作ろうとしている数式》なんだよ!」
ユーリ「数を作る?! 数って作れんの?」
僕「うん、できるんだよ。集合を使って数を作ることができる。 《数》といっても、まずは $0$ 以上の整数だけどね。 つまり、 $$ 0, 1, 2, 3, \ldots $$ という数を、集合だけを使って作ってみよう!というんだよ。これは、フォン・ノイマンという人が考えたやり方なんだ。 いわば《ノイマンの方法》だね」
ユーリ「それ、すんごく、おもしろそー!……おもしろそーな気がするんだけど、 でも、何がなんだかわかんないね」
僕「難しい話じゃないよ。ユーリなら絶対わかるから」
ユーリ「へー!」
僕「《ノイマンの方法》では、まず《空集合》つまり $\ZERO$ のことを $0$ と見なす」
《空集合を $0$ と見なす》
$$ \ZERO \LOOKSLIKE 0 $$
ユーリ「は? はあ……」
僕「それから《空集合だけを要素に持つ集合》つまり $\ONE$ のことを $1$ と見なす」
《空集合だけを要素に持つ集合を $1$ と見なす》
$$ \ONE \LOOKSLIKE 1 $$
ユーリ「……それで?」
僕「うん、それで今度は、 《ここまで出てきた集合すべてを要素に持つ集合》 を考える。 言い換えると《$\ZERO$ と $\ONE$ を要素に持つ集合》のことだね。これを $2$ と見なす」
《ここまで出てきた集合すべてを要素に持つ集合を $2$ と見なす》
$$ \TWO \LOOKSLIKE 2 $$
ユーリ「うーん……」
僕「え? そんなに難しくないだろ?」
ユーリ「いや、むずかしーとかじゃなくて、何だかつまんない」
僕「つまらないって、どうして?」
ユーリ「だって、リクツがわかんないから。 $0$ と $1$ は、 まー、何となくわかる気もするけど、 $2$ はわかんない。 何かテキトーに作ってるみたいだから、つまんない」
僕「こういうふうにして数を作っていく理由はあるよ。 ほらほら、その集合に属している《要素の個数》を考えてみればいい。 それがちょうど、その集合が表している数と一致することになる!」
《要素の個数》と《数》が一致
$$ \begin{align*} \ZERO & \LOOKSLIKE 0 \qquad \REMTEXT{要素の個数は$0$個} \\ \ONE & \LOOKSLIKE 1 \qquad \REMTEXT{要素の個数は$1$個} \\ \TWO & \LOOKSLIKE 2 \qquad \REMTEXT{要素の個数は$2$個} \\ \end{align*} $$
ユーリ「いやいやいや、それはリクツとして弱いっちや」
僕「突然の零崎軋識……零だけに」
ユーリ「だって、 集合の《要素の個数》を使って数を表したいんだったら、 $0,1,2$ は、このほうがカンタンじゃん!」
《要素の個数》で数を表したいんだったら……このほうが簡単?
$$ \begin{align*} \ZERO & \LOOKSLIKE 0 \qquad \REMTEXT{要素の個数は$0$個} \\ \bigl\{\,\{\,\}\,\bigr\} & \LOOKSLIKE 1 \qquad \REMTEXT{要素の個数は$1$個} \\ \bigl\{\,\{\,\},\,\{\,\}\,\bigr\} & \LOOKSLIKE 2 \qquad \REMTEXT{要素の個数は$2$個(?)} \\ \end{align*} $$
僕「なるほど。ユーリは賢いなあ! でも、それはまずいんだよ。 ユーリは、 $$ \bigl\{\,\{\,\},\,\{\,\}\,\bigr\} $$ という集合は要素が $2$ 個あると考えたんだけど、そうじゃないから」
ユーリ「だって、 $\{ \qquad \}$ の中に $2$ 個の要素入れたよ。 $2$ 個の空集合を要素にしたんじゃ、だめなの?」
僕「うん。それじゃだめだね。集合を考えるとき、ひとつの集合に等しい要素が何個入っていても $1$ 個として考えるルールになってるから。 もう少し正確にいうと、集合では《何かがその集合に属しているかどうか》だけに注目することになっていて、 等しい要素が何個入っているかは気にしない」
ユーリ「ふーん。個数が問題にならないって、すんごく不自然だけど、ルールならしょうがない?」
僕「それほど不自然でもないんだよ。たとえば、ユーリの同級生の中で《チョコが好きな人の集合》と、 《クッキーが好きな人の集合》を考えるとするよね。両方の集合を合わせた和集合を考えたとき、 両方の人数をそのまま足しちゃだめだよね。 《チョコかクッキーのどちらでもいいから好きな人の集合》を考える場合」
ユーリ「そりゃそーだね。だって、両方好きな人がいるかもしんないから」
僕「そうそう。両方の人数をそのまま足すんじゃなくて、 両方の集合の要素をまとめた上で《ほんとうのところは何人いるか》を考えたくなる。 《だぶり》に注意するわけだ。 それっていうのは、等しい要素は何個入っていても $1$ 個だと考えてることになる。 要素になっているかどうかは気にする。等しい要素は何個入っていても $1$ 個として考えてる」
ユーリ「確かに! そーゆー意味では不自然ではない?」
僕「うん。 だから、何かがその集合に属しているかどうかだけに注目しましょうというルールは、 それほど不自然な話じゃあないんだ」
ユーリ「ふむふむ。ちょっと納得」
僕「それで、話を戻そう。《ノイマンの方法》の話をしてたんだった。 集合を使って $0,1,2$ をこんなふうに表してみた。集合で数を作ってみたといってもいい」
集合で数を作る
$$ \begin{align*} \ZERO & \LOOKSLIKE 0 \\ \ONE & \LOOKSLIKE 1 \\ \TWO & \LOOKSLIKE 2 \\ \end{align*} $$
ユーリ「ふーん……」
僕「そして、ユーリは $2$ の作り方にひっかかっていた。 ユーリが提案した $$ \bigl\{\,\{\,\},\,\{\,\}\,\bigr\} $$ という集合だと、要素の個数は $2$ にならない」
ユーリ「うーん、そっか……空集合しか要素がないってことは、要素が $1$ 個?」
僕「そういうこと。さて、ここでユーリにクイズです」
ユーリ「クイズ!」
僕「《ノイマンの方法》では、どんな集合が $3$ になるだろうか。これがクイズ」
《ノイマンの方法》では、どんな集合が $3$ になるか?
$$ \begin{align*} \ZERO & \LOOKSLIKE 0 \\ \ONE & \LOOKSLIKE 1 \\ \TWO & \LOOKSLIKE 2 \\ \REMTEXT{???} & \LOOKSLIKE 3 \\ \end{align*} $$
ユーリ「にゃるほど? $3$ を作ろう!ってことだにゃ?」

ユーリは急速思考モードに入り、
栗色のポニーテールが金色に輝く。
ややあって、ユーリは満足げに顔を上げる。
僕「できた?」
ユーリ「できたよ! 要素数が $3$ 個になる集合を、空集合をもとにして作ればいーんでしょ? カンタン!」
ユーリの答え
$$ \begin{align*} \ZERO & \LOOKSLIKE 0 \\ \ONE & \LOOKSLIKE 1 \\ \TWO & \LOOKSLIKE 2 \\ \THREEYURI & \LOOKSLIKE 3 \qquad \REMTEXT{(?)}\\ \end{align*} $$
僕「おっと! うーむ、そうきたか……」
ユーリ「これでいーんでしょ?」
僕「うーん、これはお兄ちゃんのクイズの出し方がよくなかったかもしれない。 そもそも、《ノイマンの方法》をちゃんと説明してないしね。 確かにユーリが作った集合は要素の個数が $3$ になっている。 でも、残念ながらユーリの答えは、《ノイマンの方法》にはなってないんだ」
ユーリ「えー! じゃ、正解は?」
僕「ユーリが持ってきた、その紙に書いてある通り」
ユーリ「へ? これ? これが $3$ なの?」
《ノイマンの方法》により、集合で作った $3$
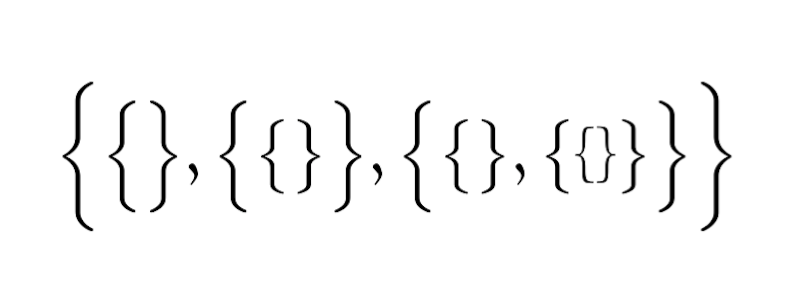
僕「そうだね」
クイズの答え(ノイマンの方法で $0,1,2,3$ を作った)
$$ \begin{align*} \ZERO & \LOOKSLIKE 0 \\ \ONE & \LOOKSLIKE 1 \\ \TWO & \LOOKSLIKE 2 \\ \THREE & \LOOKSLIKE 3 \\ \end{align*} $$
ユーリ「えー! 何かナットクいかなーい」
僕「《ノイマンの方法》をちゃんと説明しないお兄ちゃんが悪かったよ。 さっきチラッと言ったんだけどね。《ノイマンの方法》っていうのは、 《ここまで集合で作ってきた数のすべてを要素に持つ集合》を次の数と見なす、というやり方なんだよ」
ユーリ「……よくわかんない」
僕「うん。順番に話すよ。 最初に $0$ という数を作ろう。 最初に $0$ を作ろうとするとき、まだ数は $1$ 個も作っていない。 だから《要素を $1$ 個も持たない集合》を $0$ と見なすわけだ」
ユーリ「うん、まー、それは何となくわかる。要素を $1$ 個も持たない集合って、空集合でしょ?」
僕「そうそう。それで、次に $1$ という数を作ろう。 ここまで集合で作ってきた数は $0$ しかない。 だから《$0$ だけを要素に持つ集合》を $1$ と見なそう」
ユーリ「ちょっと待って。だったら $1$ は $\bigl\{ 0 \bigr\}$ ってことじゃん」
僕「そうそう! もしも $0$ が $\{\,\}$ だとしたら、 $\bigl\{ 0 \bigr\}$ は $\ONE$ になるよね?」
ユーリ「おぅふ……そんな《ものすごいこと》やっていーの? だって、数を集合にすり替えてるじゃん! $\bigl\{ 0 \bigr\}$ の $0$ のところを $\{\}$ に変えたってことでしょ?」
僕「そうそう、そういうこと。 いまは集合を使って数を作ろうとしているわけだから。 そういう《ものすごいこと》をやってもいいことにしちゃえ!」
ユーリ「へー、そーゆーの、アリなんだ!」
僕「$0$ っていうのを、 $\{\,\}$ で書いた数式に貼り付けたシールだと思ってもいいよ」
ユーリ「ペタって?」
僕「そうだね。名前付けをしてるだけ。 $\{\,\}$ の代わりに、 $0$ と名前を付けましたよってね」
ユーリ「おもしろくなってきた。そんなのアリなんだぁ……」
僕「次に $2$ という数を作ろう。これまでに作った数は $0$ と $1$ になる。 だから《$0$ と $1$ を要素に持つ集合》を考えて、これを $2$ と見なそう」
ユーリ「待って待って待って! うわ……ほんとにそーなってるね。 $\bigl\{0,1\bigr\}$ に出てくる $0$ を $\ZERO$ に変えて、 $1$ を $\ONE$ に変えると、 $$ \Bigl\{\, 0,\, 1 \,\Bigr\} $$ は、 $$ \TWO $$ になるんだ! これが $2$ なの?」
僕「そういうこと。 そして、ここまでと同じように《ノイマンの方法》を使って、次の数である $3$ を作ろう。すると……」
ユーリ「これまでに出てきた数は $0,1,2$ で、 それを要素に持つ集合を考えて、それを $3$ にしちゃう……とゆーことは、 $3$ は、 $\bigl\{0,1,2\bigr\}$ になる。そして、 $$ \Bigl\{\, 0,\, 1,\, 2\,\Bigr\} $$ は、 $$ \THREE $$ になる! 確かにこの数式じゃん!」
《ノイマンの方法》により、集合で作った $3$
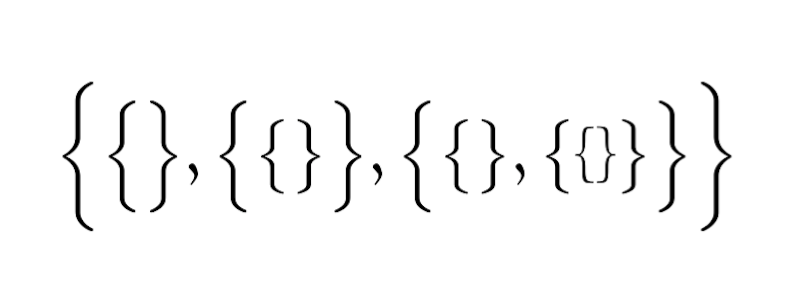
僕「ね? 空集合からスタートして、数を作っていく《ノイマンの方法》はおもしろいだろ?」
$\{0,1,2\}$ で、 $3$ を作る
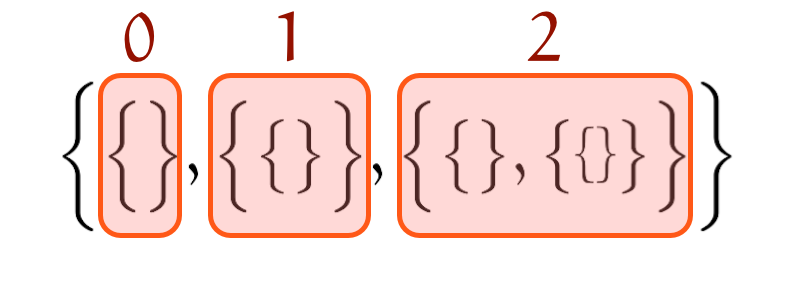
ユーリ「うん、おもしろい! やっとイミわかってきた」
僕「こういうふうにして、空集合から順番に数を作っていく《ノイマンの方法》は、 数学読み物によく出てくる話題なんだよ。 『無から有を生み出す』みたいで、かっこいいよね」
ユーリ「……」
僕「ユーリ、何を考えてるの?」
ユーリ「……ねーお兄ちゃん。さっきお兄ちゃんは、 《ここまで集合で作ってきた数のすべてを要素に持つ集合》を次の数と見なすって言ってたじゃん?」
僕「そうだね。《ノイマンの方法》は、そういうルールで一貫してる」
ユーリ「でも、そのルールでなくちゃいけないってわけじゃないよね?」
僕「うーん……まあ、そうだね」
ユーリ「たまたま、そういうルールを決めた人がいたわけでしょ?」
僕「決めた人って、だからノイマンがそれを考えたんだよ。フォン・ノイマン」
ユーリ「そのノイマンが 『こーやって数を作ってやんよ』ってルールを決めた」
僕「突然の零崎人識」
ユーリ「だったら、ユーリがルール決めてもいいよね? イッカンしてれば」
僕「ほう」
ユーリ「宣言。ユーリは、こんなふーにして、 $0$ 以上の整数を空集合から作りまーす! 《ユーリの方法》だっ!」
ユーリの方法
$$ \begin{align*} \YZERO & \LOOKSLIKE 0 \\ \YONE & \LOOKSLIKE 1 \\ \YTWO & \LOOKSLIKE 2 \\ \YTHREE & \LOOKSLIKE 3 \\ & \vdots \\ \end{align*} $$
僕「なるほど……」
ユーリ「ひらめいたのさっ! 《ユーリの方法》は、 《一つ前に作った数だけを要素に持つ集合を次の数にする》というの。 つまり、 $1$ は $\{ 0 \}$ で作り、 $2$ は $\{ 1 \}$ で作り、 $3$ は $\{ 2 \}$ で作る! ……ね? これでもイッカンしてるっしょ?」
僕「うん。うんうん。うんうんうん。 これはこれで確かに一貫したルールで、空集合から $0$ 以上の整数を作っているといえる。すごいぞユーリ。 ただ……」
ユーリ「ただ?」
僕「《ユーリの方法》では、《要素の個数がそのまま数にもなってる》とはいえない。そこが《ノイマンの方法》より弱いといえば弱いかも」
ユーリ「あ、またそれを持ち出す……うー」
僕「いや、でも、この《ユーリの方法》でも悪いってわけじゃないよ。こういうのを考えられるのはすごいと思う」
ユーリ「うー……わかったっ! バージョンアップする!」
僕「?」
ユーリ「こーすればいい! さっきのは《ユーリの方法》バージョン $1$ ね。こんどは《ユーリの方法》バージョン $2$ 登場!」
《ユーリの方法》(バージョン $2$)
$$ \begin{align*} \ZERO & \LOOKSLIKE 0 \qquad \REMTEXT{要素の個数は$0$個}\\ \ONE & \LOOKSLIKE 1 \qquad \REMTEXT{要素の個数は$1$個}\\ \TWO & \LOOKSLIKE 2 \qquad \REMTEXT{要素の個数は$2$個}\\ \THREEYURI & \LOOKSLIKE 3 \qquad \REMTEXT{要素の個数は$3$個}\\ & \vdots \\ \end{align*} $$
僕「……」
ユーリ「ほーらね! バージョン $2$ なら、 イッカンしたルールで、空集合から順番に作って、しかも要素の個数がちょうどその数になってるっしょ?」
僕「ユーリ……ユーリは、ほんとに賢いなあ!」
ユーリ「へっへー。もっとホメて」
僕「がく。でも、このバージョン $2$ って、さっき出したクイズの《ユーリの答え》と同じだよね」
ユーリ「え? あらほんと」
僕「この方法は確かに、一貫性があって、空集合から順番に作り、要素の個数がちょうどその数になってる。 すごい。ただ……」
ユーリ「ただ?」
僕「《ユーリの方法》バージョン $2$ を見てあらためて気付いたんだけど、《ノイマンの方法》はすごくすぐれている。 《ノイマンの方法》だと、《次の数》を作るときに加えていく要素は必ず《数》なんだ。 だから、いわば、数を集めて次の数を作る形になってる。 でも《ユーリの方法》バージョン $2$ だと……」
ユーリ「同じだよ! 加えていく要素は数を作るのに使った集合だけでしょ?」
僕「いや、違うんだよ。 $3$ を作るときに加えた要素 $\YYADDED$ は、《ユーリの方法》バージョン $2$ では数じゃない。 $0$ でも、 $1$ でも、 $2$ でもないよね?」
ユーリ「え? あっ! ほんとだ……」
母「子供たち、おやつよ!」
僕「おやつにしようか」
ユーリ「する……」
僕とユーリはクッキーを食べながら話を続ける。
僕「ところで、空集合から数を作っていく《ノイマンの方法》だけど、これだとまだ《数》って感じがしないよね」
ユーリ「どゆこと? 一貫したルールで、 $0,1,2,3,\ldots$ を作れるよ?」
《ノイマンの方法》で $0,1,2,3,\ldots$ を作る $$ \begin{align*} \{\,\} & \LOOKSLIKE 0 \\ \{\,0\,\} & \LOOKSLIKE 1 \\ \{\,0,1\,\} & \LOOKSLIKE 2 \\ \{\,0,1,2\,\} & \LOOKSLIKE 3 \\ \{\,0,1,2,3\,\} & \LOOKSLIKE 4 \\ \{\,0,1,2,3,4\,\} & \LOOKSLIKE 5 \\ & \vdots \\ \end{align*} $$
僕「うん。《互いに異なるものを、順番に作り出せる》ことはわかった。 でも、数ってそういうものだっけ?」
ユーリ「数って、どーゆーものだっけ?」
※今回登場した《ユーリの方法》(バージョン $2$ じゃないほう)は、数学者ツェルメロが考えた方法になります。 いわば《ツェルメロの方法》ですね。
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第151回終わり)
(2016年4月8日)
この記事は『数学ガールの秘密ノート/数を作ろう』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!