第150回 シーズン15 エピソード10

波の広がり（後編）

図書室

僕「ともかく、答えをまとめてみるよ」

テトラ「……」

ミルカ「……」

僕「そうだ。具体例に進もうよ！　僕が具体例を持ってる。 先日、ユーリと遊んだときにちらちらと見えていた《波》だ。 この平らな波をフーリエ展開してみよう！」

ミルカ「ふむ、それもいいが、その前にやることがある」

僕「やること？」

ミルカ「この《解答1（？）》の誤りを一つ見つけること。フーリエ展開の可能性という話ではなく、単純な誤りを」

僕「単純な誤りがあるって？」

テトラ「……」

僕「収束条件ではないんだよね？」

ミルカ「フーリエ展開ができる $f(x)$ の条件ではないし、 関数の収束条件でもない。もっと単純で、明白な誤りがある」

テトラ「あ、あのですね……《$n$ の条件》でしょうか？」

ミルカ「テトラはそれを具体的に言う」

テトラ「あたしが計算していた定積分では、 $m$ も $n$ も《$1$ 以上の整数》という条件が付いていました。 でも、先ほどの先輩の解答1（？）では、 $a_n$ や $b_n$ に対する $n$ に何も条件が付いていなかったので……」

僕「ちがうよ、テトラちゃん」

ミルカ「そこだよ、テトラ」

僕「あれ？　確かにさっきの解答では条件を付けなかったけど、 $n$ は $0$ 以上の整数にして構わないはずだよ」

ミルカ「$n=0$ でも？」

僕「大丈夫。だって、 $\cos nx=\cos 0x=1$ だし、 $\sin nx=\sin 0x=0$ になるだけのことだから。 つまり、 $n=0$ のときは自動的に、 $$\{\begin{array}{ll}{a}_0& ={\displaystyle \frac{1}{\pi }}{\int }_0^{2\pi }f(x)\cos 0xdx\\ & ={\displaystyle \frac{1}{\pi }}{\int }_0^{2\pi }f(x)dx\\ b_0& ={\displaystyle \frac{1}{\pi }}{\int }_0^{2\pi }f(x)\sin 0xdx\\ & =0\end{array}$$ になってくれる。つまり $f(x)$ の定数項として、 $a_0$ を作り出すことができるはず。 これは、 $\sum$ と $\int$ の交換や関数の収束を前提とすれば、 証明もできるはずだよ」

ミルカ「どんなふうに？」

僕「こんなふうに……ええと、要するに、 $$f(x)=\sum _{k=0}^{\mathrm{\infty }}(a_k\cos kx+b_k\sin kx)$$ に対して $${\displaystyle \frac{1}{\pi }}{\int }_0^{2\pi }f(x)dx$$ という定積分を実行すればいいんだよ。それでちゃんと $a_0$ が出てくるから」

テトラ「それは先ほどやったような……（第149回参照）」

僕「うん、さっきは一般的にさらっと書いたから、 $n=0$ のときを明示的にやってみればいいだけのこと。この定積分だね」

僕「これで $k=0$ の項だけを外に出して、 $\cos 0x=1$ と $\sin 0x=0$ を使う」

テトラ「……」

僕「次に、積分と和の交換。ここはほんとうはちゃんと証明が要るはずだけど」

ミルカ「……」

僕「この $\sum$ の中は $k$ 回振動する $\cos$ や $\sin$ だから、 $0$ から $2\pi$ まで積分したら結局 $0$ になる。残りは定数の積分だから……」

僕「えっ！？」

テトラ「定積分の結果、 $a_0$ が出てくるはず……ですが？」

僕「$2a_0$ になってしまった……」

ミルカ「だから、そこが誤り。いま君が計算してくれたとおり、 $n=0$ のとき、同じ式ではフーリエ係数は得られない。 同じ式では $2$ 倍になってしまう。だから、フーリエ係数を求める式はこれが正しい。 $a_0$ の分母に注意」

僕「うわ、 $a_0$ だけ違うのか！　これは、意外な落とし穴だなあ……」

テトラ「条件を確認するのは大事なんですね……」

ミルカ「$a_0={\displaystyle \frac{1}{\pi }}{\int }_0^{2\pi }f(x)dx$ のままで行くなら、 $$f(x)=\frac{a_0}{2}+\sum _{k=1}^{\mathrm{\infty }}(a_k\cos kx+b_k\sin kx)$$ のように表す方法もある」

僕「なるほど」

矩形波のフーリエ展開

ミルカ「話が飛んでしまった。君がフーリエ展開したいといってた波があったね」

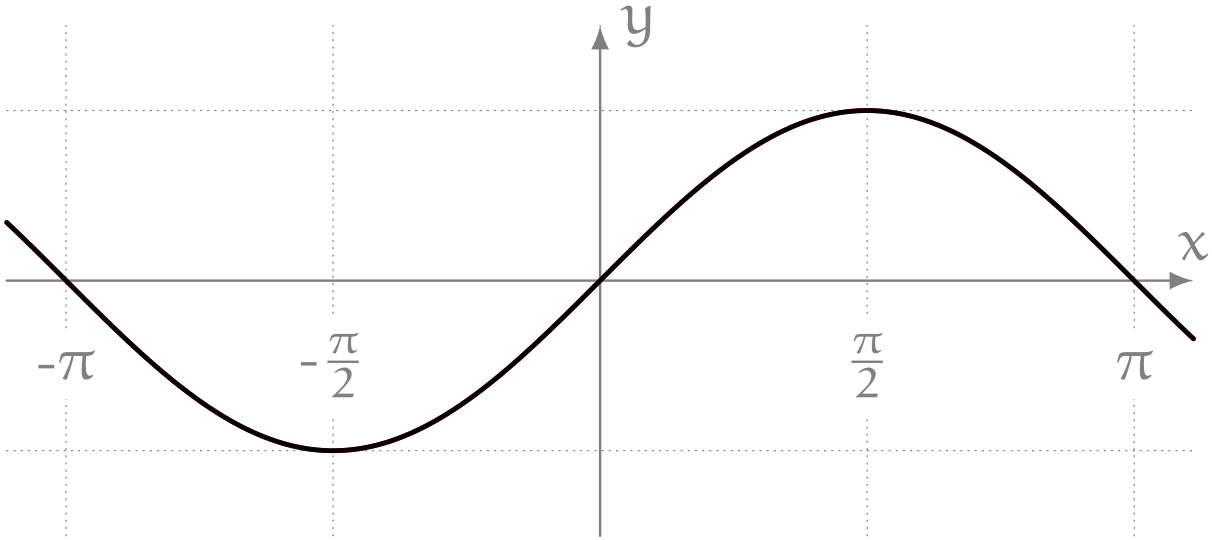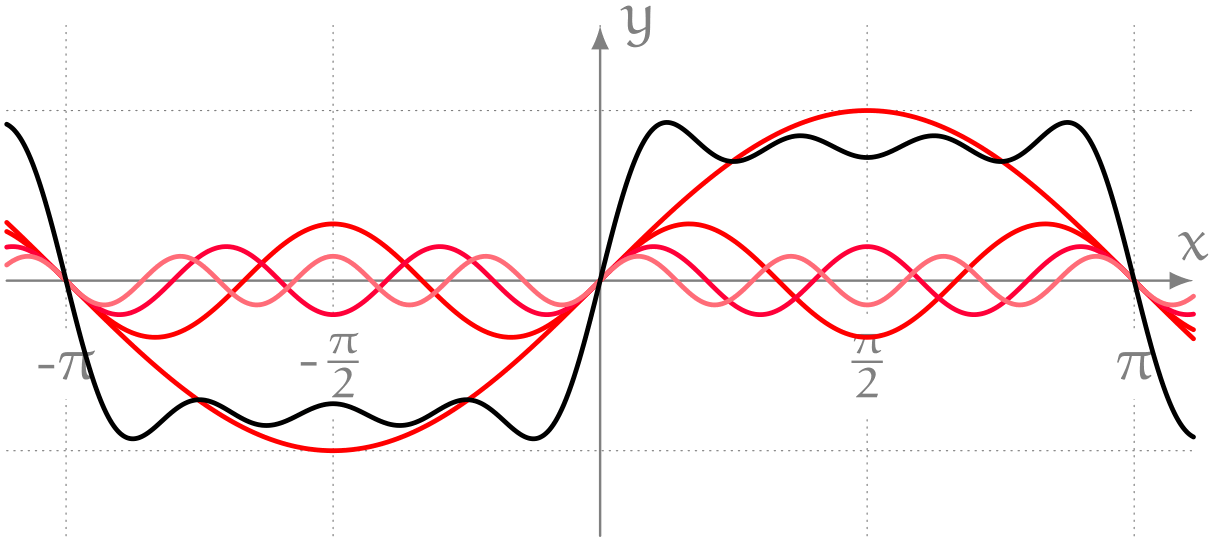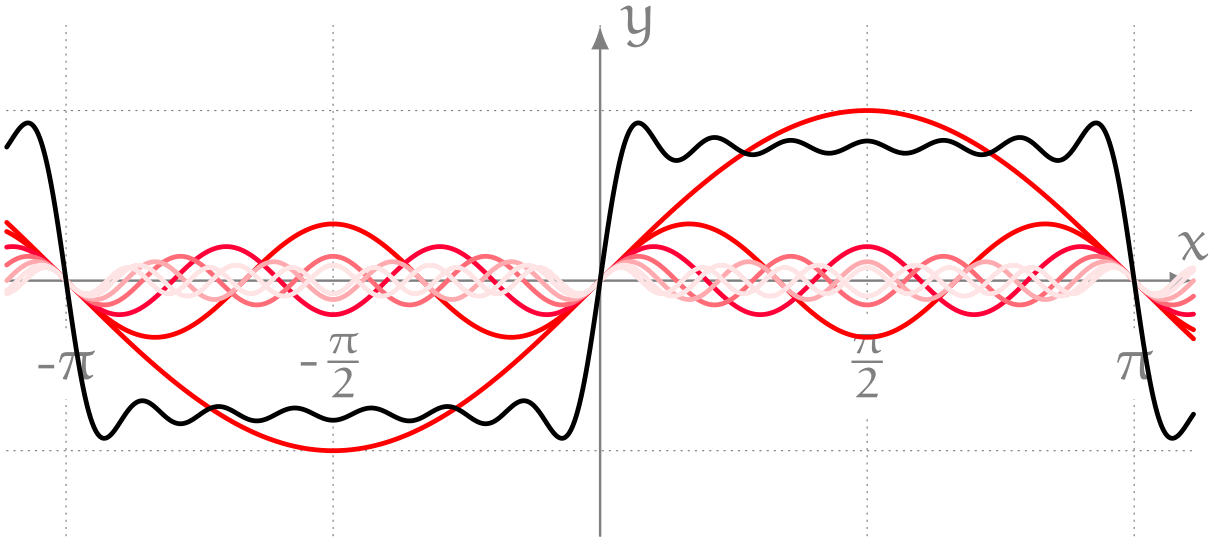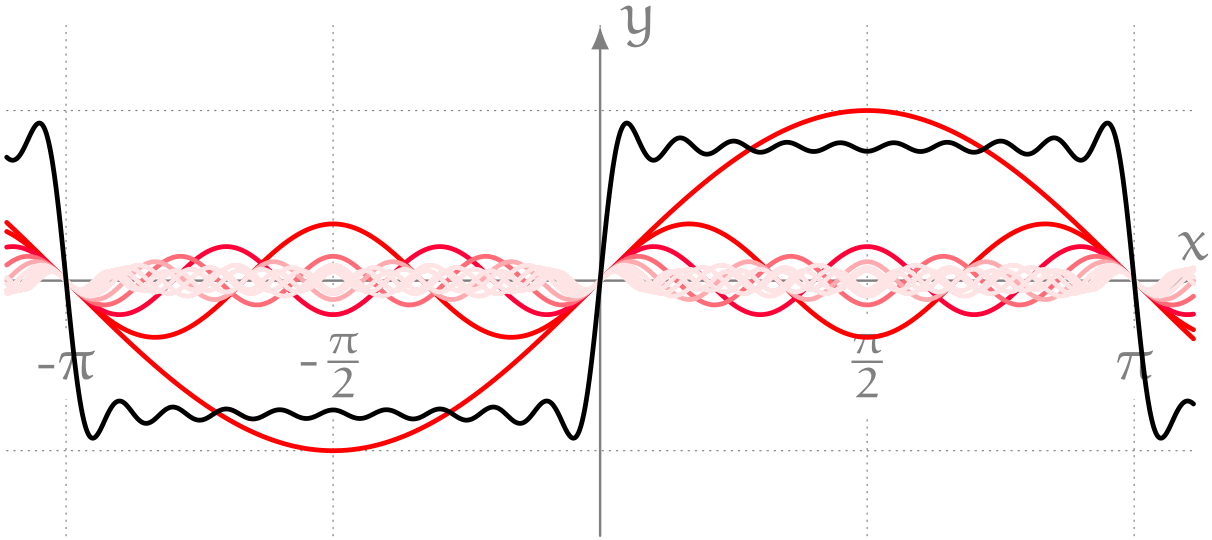
僕「そうそう。これはね、このあいだユーリと遊んでいたときに気になってた波なんだ。 $$\frac{\sin 1x}{1}+\frac{\sin 3x}{3}+\frac{\sin 5x}{5}+\cdots$$ のように奇数 $n$ を使って $\frac{\sin nx}{n}$ の和を作ると、 こんなふうに四角い波っぽくなったんだよ」

ミルカ「ふむ」

僕「だから、こういう平らな波を考えてみたいんだ」

ミルカ「矩形波（くけいは）だね」

僕「矩形波？　うん、だから、その矩形波のグラフを $y=f(x)$ だと考えれば、 フーリエ展開の方法で ${\displaystyle \frac{\sin nx}{n}}$ という形の項が出てくるんじゃないかって……そう思わない？」

ミルカ「それは確かに出てきそうだな」

僕「だよね」

テトラ「せ、先輩方！　ただいま、テトラは置いてけぼりになりかけています！　しばし、お待ちを！　頭を整理させてください」

• あたしたちは波の重ね合わせが作る波のことを考えています。
• 特に、サインカーブを作りだしている $\sin$ と $\cos$ という三角関数の重ね合わせに注目してきました。
• もう少し正確には、 $\sin nx$ と $\cos nx$ という関数です。
• これは、 $x$ が $0$ から $2\pi$ まで動く間、 $n$ 個の波を作る関数です。
• それらを加えていって……ええと？

僕「係数を掛けた上で加えるんだね」

ミルカ「線型結合」

テトラ「あ、そうでした。そうでした」

• $a_0\cos 0x+b_0\sin 0x+a_1\cos 1x+b_1\sin 1x+\cdots$ のように加えていきます。
• 三角関数のそのような和が、波の重ね合わせとなって、ある一つの関数 $f(x)$ になったとします。
• それは、つまり、 $f(x)=\sum _{k=0}^{\mathrm{\infty }}(a_k\cos kx+b_k\sin kx)$ という形です。
• $f(x)$ をこのように表現するのがフーリエ展開です。
• ここで大事になってくるのが $a_0,a_1,a_2,\dots$ と $b_0,b_1,b_2,\dots$ という数列です。
• この数列が $f(x)$ を表すことになるからです。
• それから、ええと、あとは……

僕「数列 $a_n$ と $b_n$ を求める方法だね」

ミルカ「フーリエ係数」

テトラ「ですね！」

• フーリエ係数 $a_n$ と $b_n$ を求めるのに、先ほどの解答1のような定積分を使います。
• （そうでした、そうでした。 $m\ne n$ と $m=n$ のときで $\cos mx\cos nx$ や、 $\sin mx\sin nx$ などの定積分を場合分けしました）

僕「そしてこれから、矩形波を実際に定積分して、ほんとうにフーリエ係数が求まるかを試してみようとしているわけだね」

テトラ「ふう……ようやく先輩方に追いつきましたっ！」

ミルカ「問題を立てると、こうなるな」

テトラ「……先輩、でも、こんなにがたがたになった関数の積分なんてできるんですか？　あたしができる積分というのは、 $x^2$ や $e^x$ や $\sin x$ や $\cos x$ や……ぜんぶ、つながった関数なんですけれど」

僕「うん、そうだね。僕たちがふだん問題で解くのはつながった関数……連続関数のことが多いけど、 これは大丈夫。積分区間で分けて考えればいいんだよ。 ほら、たとえば、 $x$ が $0$ から $\pi$ までの範囲では、 $f(x)$ は $1$ という《定数関数》になるよね？」

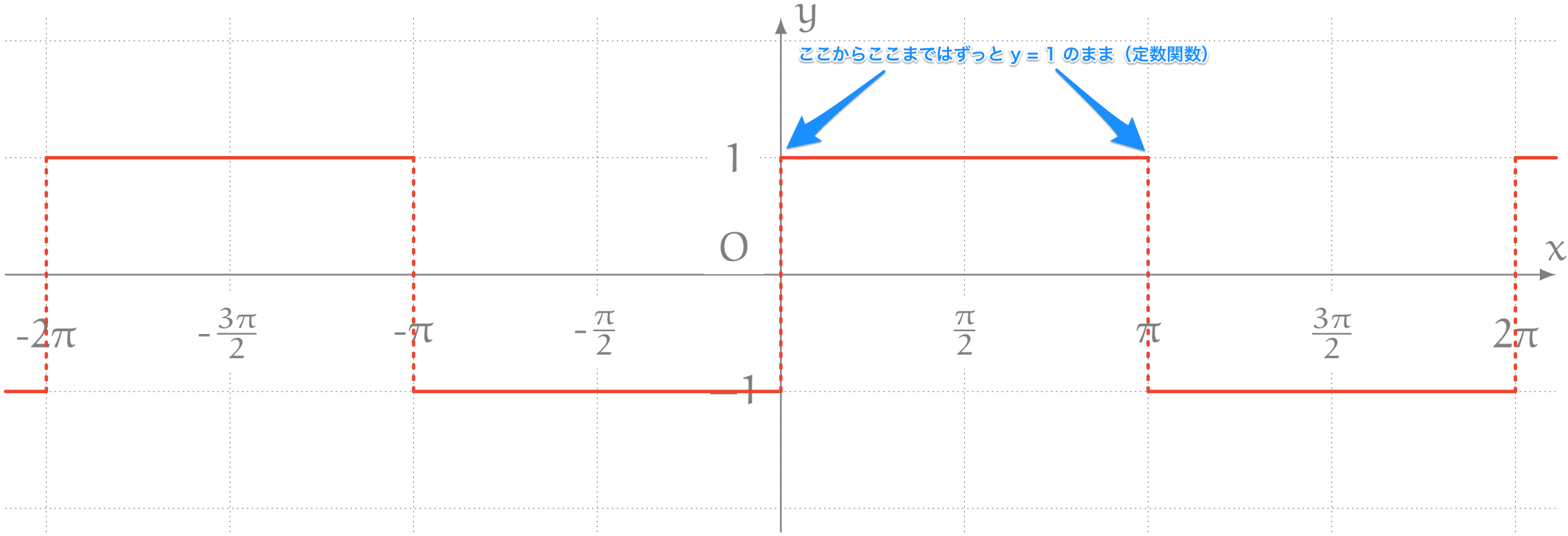
テトラ「……あっ、そうですね。定数関数の積分はあたしもできます！　ははあ……ここにも《場合分け》が出てくるんですね」

僕「積分は結局は和なんだから、積分区間で足せばいいし」

ミルカ「まず、 $f(x)$ を……」

僕「そうだね。まず $f(x)$ を式で表さないと。やみくもに積分積分と言ってもばかりいてもしょうがないから。 グラフから、たとえばこんなふうに書けるね。 $$f(x)=\{\begin{array}{llll}1& & & 2n\pi \leqq x<(2n+1)\pi \\ -1& & & (2n+1)\pi \leqq x<2(n+1)\pi \end{array}$$ ただし、 $n$ は整数」

テトラ「ちょっとお待ちください。 $n=0$ のときは $0\leqq x<\pi$ で $f(x)=1$ で、 $\pi \leqq x<2\pi$ で $f(x)=-1$ ですね……はい、わかりました。 これは《$\pi$ の偶数倍》と《$\pi$ の奇数倍》の範囲をつなぎあわせているんですね」

僕「$a_0$ から行くよ。これは一瞬だね」

ミルカ「ふむ。 $f(x)$ は奇関数だから、 $0$ になるのは予想が付くな」

僕「なるほどね。偶関数である $\cos nx$ の係数は $0$ になるわけだね」

ミルカ「もちろん、いまは計算練習をしているわけだから、それは検算用の考えになるけれど」

テトラ「あ、あの、 $b_0$ も一瞬です！」

ミルカ「$0$ だからな」

僕「$0$ だからね」

テトラ「……です」

僕「じゃ、今度は $n=1,2,3,\dots$ のときの $a_n$ を求めるよ。 基本はさっきと同じように積分区間を分けるんだけど、今度は $\cos nx$ が出てくるわけだよね」

僕「うん、やはり予想通り $0$ になったね」

テトラ「……先輩、この途中の式なんですが」

テトラ「これって、このようにマイナスを前に出すことができますよね？」

僕「うん、そうだね」

テトラ「だったら、同じ $\cos nx$ という関数を積分しているんですから、 ${\int }_0^{\pi }$ と ${\int }_{\pi }^{2\pi }$ という二つの積分区間を一つにまとめて ${\int }_0^{2\pi }$ にしてもいいですよね。 つながっている区間で同じ関数を積分するんですから。 それなら、一気に $0$ だと求められますよ！」

僕「ああなるほど……じゃない、それはだめだよ、テトラちゃん。 そんなことをしたら、二つの関数を別の区間まで伸ばして積分してることになるから」

テトラ「え……？」

ミルカ「それでは伝わらない。テトラの混乱は、一般的に書けばすぐ解ける。 いまテトラがやろうとした積分の操作はこれだ。こんなことはできない」

テトラ「あっ、そうですね。うっかりしました。 $\cos nx$ という同じ顔を見てしまったもので……」

ミルカ「ここまでで $a_0=a_1=a_2=\cdots =0$ が得られた。偶関数の成分はすべて $0$ だ」

僕「いよいよ $b_n$ だね」

テトラ「あ、あたし、計算します！　式の途中までは先ほどと同じですから……」

テトラ「あ、あれれ……？　あたし、計算ミスしてます？」

僕「どうして、そう思ったの？」

テトラ「だって、 $\cos$ が出てしまいました。先輩、先ほど $\frac{\sin nx}{n}$ になるとおっしゃってませんでしたか？　 $\sin$ が出るはずなのに、 $\cos$ が出てきました！」

僕「テトラちゃん、テトラちゃん、落ち着いて。さっき僕がいった $\frac{\sin nx}{n}$ というのは、 和の各項だから、係数には $\sin$ は出てこないよ。 $\sin nx$ の係数は $\frac{1}{n}$ だね」

テトラ「だったら、なおさらです。 $\cos$ が出てきたら……」

ミルカ「テトラは $\cos n\pi$ が三角関数に見えるのか」