![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/積分を見つめて』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。好奇心旺盛で根気強い《元気少女》。
僕とテトラちゃんは図書室でおしゃべりをしている。 区分求積法を使って簡単なグラフが作る形の面積を計算した話だ。
僕「……そんな計算をしたんだよ(第134回参照)。ちょっとややこしいけれど、 ちゃんと面積が求まるのがおもしろいんだ」
テトラ「ユーリちゃんってすごいですね。何でも理解できちゃうんですから。 区分求積法から極限まで!」
僕「区分求積法は、名前は難しそうに見えるけど、直観的にもわかりやすいしね。 ほら、短冊のように長方形が見えて《はさみうち》するからね」
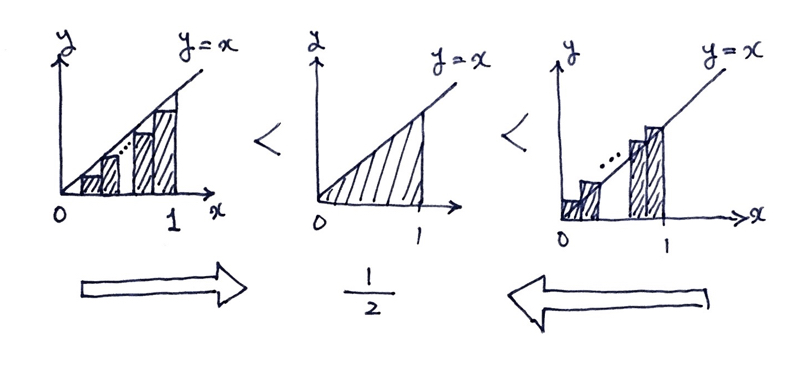
テトラ「そういう方法で三角形の面積がきちんと求められるんですね」
僕「そうだね。一辺の長さが $1$ の直角二等辺三角形の面積は $\frac12$ になる」
テトラ「でも、三角形の面積を求めるのに、 いつも区分求積法を使うとしたら大変ですね」
僕「ああ、ユーリも同じようなこと言ってたなあ。 確かにそうなんだけど、積分という方法に一般化してあれば、 どんな形のグラフでも面積を求めるときに同じ方法が使えるからね。 そこがいいところなんだと思うよ」
テトラ「あ、いえ、すみません。そういう意味ではないんです」
僕「というと?」
テトラちゃんはそこで口をつぐむ。
ちょっぴり首をかしげ、しばらく考えてからゆっくり話し出した。
テトラ「あのですね、区分求積法のお話はわかったと思います。面積を求めるための方法。 グラフの形ごとにひとつひとつ公式を作るんじゃなくて、 積分というたった一つの便利な《武器》があれば、 しっかり面積を求められます。 でも、それはそうだとしても、毎回、 区分求積法を行うのはたいへんな計算ではないかと思ったんです。 たとえば、先ほどの先輩のお話で、 $1^2+2^2+3^2+\cdots+n^2$ という計算が出てきました(第134回参照)。 その和を利用して極限値を求める……それはそれで難しい話ではないのでしょうか?」
僕「まあ、そうだね。それは確かに。 でもほら《積分は微分の逆》だから、 微分してその関数になるような関数を見つければいいんだよ」
テトラ「積分は、微分の、逆……」
僕「そうだよ。積分して微分すれば元に戻る。定数の差をのぞけば」
テトラ「あ、あれ……わからなくなってしまいました。 積分は面積を求めるものですよね」
僕「うん、ここではそうだね」
テトラ「積分は面積を求めるもので、先ほども $\frac12$ という具体的な面積を求めました。 でも、積分は微分の逆というのは? だって、あの、 $\frac12$ を微分したら $0$ になってしまいますよね。 定数の微分は $0$ なんですから。それは……あれ?」
僕「ああ、違う違う。そうだね、確かに $\frac12$ という定数を微分したら $0$ になっちゃう。 それは僕が悪かった。言葉をちゃんと補って話すべきだったね。 じゃ、最初からちゃんと説明するよ」
テトラ「はい!」
僕「僕とユーリが計算していたのは、たとえば $y = x$ というグラフが $0 \leqq x \leqq 1$ の区間で作り出す形の面積だったんだよ」
テトラ「はい、それはわかります。直角二等辺三角形」
僕「つまりそれは $x$ が動く範囲を固定して考えていたわけだね」
テトラ「固定……といいますと?」
僕「うん、 $0 \leqq x \leqq 1$ という区間を決めて計算したということ。 三角形の大きさは決まっている。でもたとえば、右端を $1$ じゃなくて $2$ や $3$ にしてもいいよね。 もちろんそのたびごとに面積は変わるわけだけど」
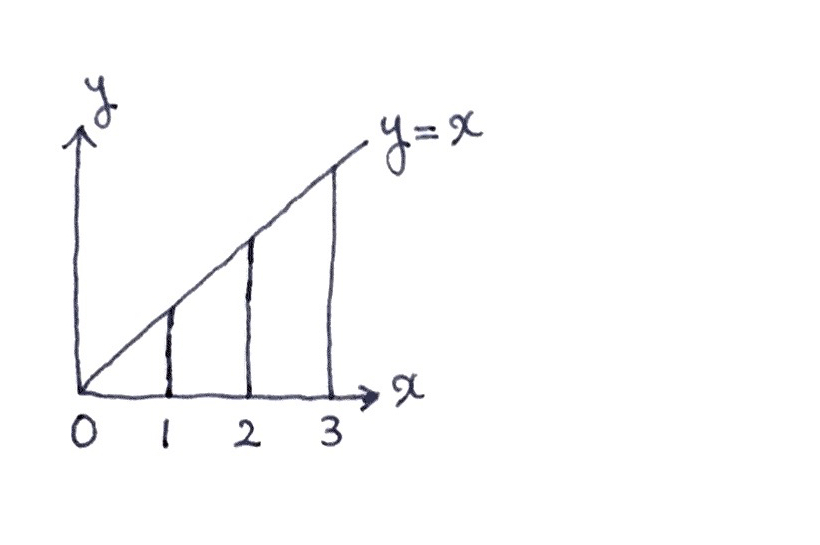
テトラ「はい、それはそうですね。三角形が大きくなって」
僕「だから、たとえば右端を $a$ という文字で表して考えることもできるよね。 そのとき面積は……」
テトラ「$\frac{a^2}{2}$ になります」

僕「そうなる。 それは三角形の面積の公式で考えてもいいんだけど、 いまは $0 \leqq x \leqq a$ の区間で区分求積法を使って求めたと考えてみる」
テトラ「はい」
僕「それでね、テトラちゃん。 ここからおもしろくなってくるんだけど、この場合の《三角形の面積》は《$a$ の関数》といえるよね。 なぜなら、 $a$ の具体的な値が一つ決まれば、三角形の面積が一つ決まるから。 関数ってそういうものだよね」
テトラ「あ、はい……あの、先輩。ここまではまだ難しい話じゃないですよね。 あたしは先輩のお話の意味はよくわかっているつもりなんですが、難しい話は出てきてないですよね?」
僕「うん、大丈夫。まだ難しい話は何も出てきてないよ。 $y = x$ のグラフが作る三角形の面積は $\frac{a^2}{2}$ になる。 $a$ を大きくしていけば、面積も大きくなる。 そのようす……つまり、三角形の面積を $a$ の関数としてグラフにしてみると、 $y = \frac{a^2}{2}$ で表される放物線になるわけだね」
テトラ「はい……わかります。その通りだと思います」

僕「じゃ、ここで、 $\frac{a^2}{2}$ という $a$ の関数に名前を付けて $F(a)$ と呼ぶことにしよう。 つまり、 $$ F(a) = \frac{a^2}{2} $$ と定義するんだね。 おっと、うーん、このまま $a$ で話を進めてもいいんだけど、 変化する量が $a$ という文字だと落ち着かないから、 $x$ にしておくね。 つまり、 $$ F(x) = \frac{x^2}{2} $$ ということ」
テトラ「それって、どんな文字にしてもいいんですか?」
僕「いいよ。いまは $F$ という関数の形の話をしているんだから、 $t$ という文字を使って、 $$ F(t) = \frac{t^2}{2} $$ にしてもいいし、何だったら、 $$ F(\heartsuit) = \frac{\heartsuit^2}{2} $$ でもいい」
テトラ「ハートマーク、いいですね! $\heartsuit\heartsuit\heartsuit$ !!」
僕「ここまで考えてくると《積分は微分の逆》を、もうすこし説明できるよ。 さっきテトラちゃんは $\frac12$ という定数を微分しちゃったけど、 そうじゃないんだ。面積を表している $F(x)$ という $x$ の関数を、 $x$ で微分するんだ」
テトラ「ということは、 $\frac{x^2}{2}$ を $x$ で微分する……」
僕「そうそう。微分した結果は $x$ になる。 おもしろいことに、 これが $y = x$ というグラフを作り出す関数になってるんだよ! うん!」
テトラ「せ、先輩……あたし、わかってないみたいです。 先輩のお話ひとつひとつはわかるんですが、全体がわからないです。 胸の中がもやもやっとして……」
僕「え。うーん……」
テトラ「すみません」
僕「いや、テトラちゃんは謝らなくていいよ。 僕の説明が悪いんだから」
テトラ「……」
僕「そうだなあ……もしかすると、 テトラちゃんは、ひとつひとつがわかっちゃうから全体がわからないのかも」
テトラ「?」
僕「テトラちゃんは《積分は微分の逆》という言葉も知っちゃったし、 $\frac{x^2}{2}$ を微分したら $x$ になるというのも知ってる。 だから《積分して→微分して→元に戻る》というのがあたりまえに見えるんじゃないかな」
テトラ「あ、そうかもしれません。 積分が微分の逆だとしたら、積分して微分したら元に戻るのは……あたりまえ、みたいで。 ですから、先輩が《おもしろいよね》とおっしゃったことの、どこがおもしろいかわからないんです。 あたりまえの話をしてて、笑いどころのわからないジョークのようです」
僕「……ごめんね」
テトラ「い、いえいえっ! そういうつもりで言ったんじゃないです!」
僕「そうだなあ……むしろ $x$ のような具体的な形じゃなくて、 $f(x)$ のように書いたほうがわかるかも。 さっき説明したことを二つに分けていえば、こうなるんだよ、テトラちゃん」
(1)《関数 $f(x)$ が作る図形の面積》を区分求積法で求めたものを、 $F(x)$ と書いた。

(2) $F(x)$ を $x$ で微分してみたら、 $f(x)$ になった。

テトラ「……」
僕「どう?」
テトラ「もしかして、これって、《ぜんぜん関係ないものが結びついているというお話》……なんでしょうか?」
僕「おお?」
テトラ「わかってきました! こういうことですね。 区分求積法で面積を求めました。でもそれは一つの図形の面積を求めるだけじゃなくて、 右端がどんな数でも面積がさっとわかるように関数の形にしておきます。それが $F(x)$ ですよね」

僕「そうそう、それでいいよ。 $x$ が決まれば面積 $F(x)$ も決まる」
テトラ「それで、面積を求める話はちょっとこっちに、置・い・と・い・て、 この $F(x)$ という関数を微分してみましょう! というのですね。 そうしたら、あら不思議。なぜか最初のグラフを作る関数 $f(x)$ が出てきちゃいました!」

僕「うん、そういうこと。そこがおもしろいんだよ!」
テトラ「はい……わかりました。《面積を求める》ということと《微分する》ということとは、 一見まったく関係ないもの。 それなのに、面積を表している関数を微分すると、元の関数にもどる」
僕「そうだね」
テトラ「《面積を求める》を《積分する》というなら、 《積分して微分すると元に戻る》といえる」
僕「その通り。そこまでいくと《積分は微分の逆》と要約できる」
テトラ「先輩、あたし、わかっちゃいました。あたしが混乱した理由です。 《積分は微分の逆》から考え始めてはいけなかったんですね」
僕「なるほど?」
テトラ「そうじゃなくて……《積分》と《微分》という二つのものがある、 というところから考えるべきだったのではないでしょうか。 一見、この二つは無関係に見えるのですが、 でも、よくよく調べてみると、 この二つは逆の関係になっていることがわかりましたっ!……という驚き? 《積分は微分の逆》なのですっ!……という不思議?」
僕「すごい、すごい! そういうこと、そういうこと」
そこで、テトラちゃんはまた考え込んだ。
僕「どうしたの?」
テトラ「……《積分は微分の逆》という言葉だけ聞くと、そういうものなのか、って思っちゃいそうになります。 なぜかというと、たとえば《足し算は引き算の逆》とか《割り算は掛け算の逆》と同じように聞こえますから。 だから、わかったような気持ちになります」
僕「そうだね。そしてさっきテトラちゃんはそれで混乱したわけだね」
テトラ「はい、そうだと思います。 もっとも、《面積を求めること》がどうして《微分すること》の逆なのか、 と考えると、それはそれで、あたしはわかってないんですけど……」
僕「テトラちゃんの《わからない最前線》が別のレベルに移ったんだね!」
テトラ「あの、先輩。こういう質問って意味ありますか。 《区分求積法で面積を求めること》の逆が、どうして《微分すること》になるのか、という質問です」
僕「もちろん、意味はあるよ。これは証明できることだから……厳密な証明は僕にはできないけど、 おおよその説明くらいならできると思う」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2015年10月30日)
この記事は『数学ガールの秘密ノート/積分を見つめて』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!