第95回 シーズン10 エピソード5

領域の利用、一気に（前編）

僕の部屋

僕「ユーリ、なに遊んでるの？」

ユーリ「……」

僕「無言か。ゲームだな」

ユーリ「……いま忙しいから、あとで」

僕「ひとの部屋に来て『忙しいから』もないと思うんだけどな。何のゲーム？」

ユーリ「あっ！　やられた！　話しかけないでって言ったのにー！」

僕「やっぱりゲームか。どんなの？」

ユーリ「お掃除ゲーム。この大きな丸いのを動かして、 この小さなフワフワを食べてくんだよ。 食べてくと、この丸いのはどんどん大きくなる」

僕「なるほど。時間内に全部食べればいい？」

ユーリ「そーそー。でも、大きくなると、角のが食べにくくなるから、 小さいうちに食べとかなきゃいけないの」

僕「やってみたいな」

ユーリ「お兄ちゃんは勉強で忙しいんでしょ？　……ま、一回だけなら貸したげてもいーよ」

僕「どれどれ……あれ？　これは？」

ユーリ「うわー、いきなりレッド食べますか。それ食べるとしびれて動けなくなる。アウトー」

僕「知らないよ、そんなの！」

円の半径

僕「食べるたびにこの円は $r$ が大きくなっていくんだね」

ユーリ「アール？」

僕「円の半径だよ。 ほら、円の方程式は $x^2+y^2=r^2$ って書くだろ。あの $r$ だよ」

ユーリ「お兄ちゃん、こないだ円の方程式は $x^2+y^2=1$ って言ってなかった？」

僕「それは半径が $1$ の場合だね。つまり、単位円のとき。 そのときは半径 $r$ が $1$ に等しいから、 $x^2+y^2=r^2$ という式は、 $x^2+y^2=1$ と書けることになる」

ユーリ「あーそかそか。それだけのことね」

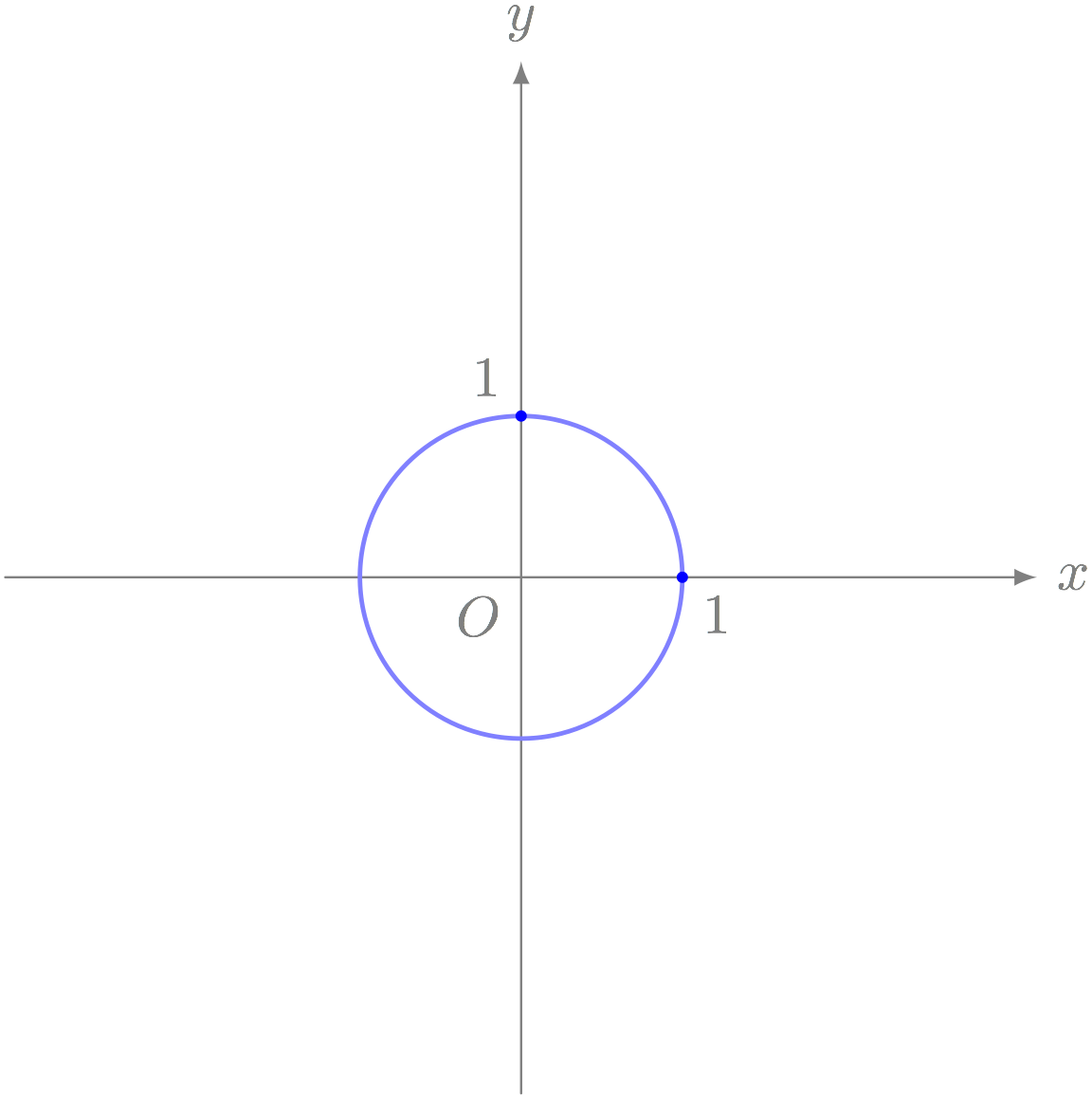
僕「ユーリのこのゲームだと、円がどんどん大きくなっていくよね。 ということは、この $r$ がどんどん大きくなっていってるといえるね」

ユーリ「$r$ が $1,2,3,\dots$ みたいに？」

僕「そうそう。もちろん、そんなふうに正の整数の値を取らなくてもいいよ。 $1.5$ とか $3.7$ みたいな値でもいい。とにかく $r$ が大きくなれば、 $x^2+y^2=r^2$ という方程式が表す円は大きくなっていく」

ユーリ「ふーん」

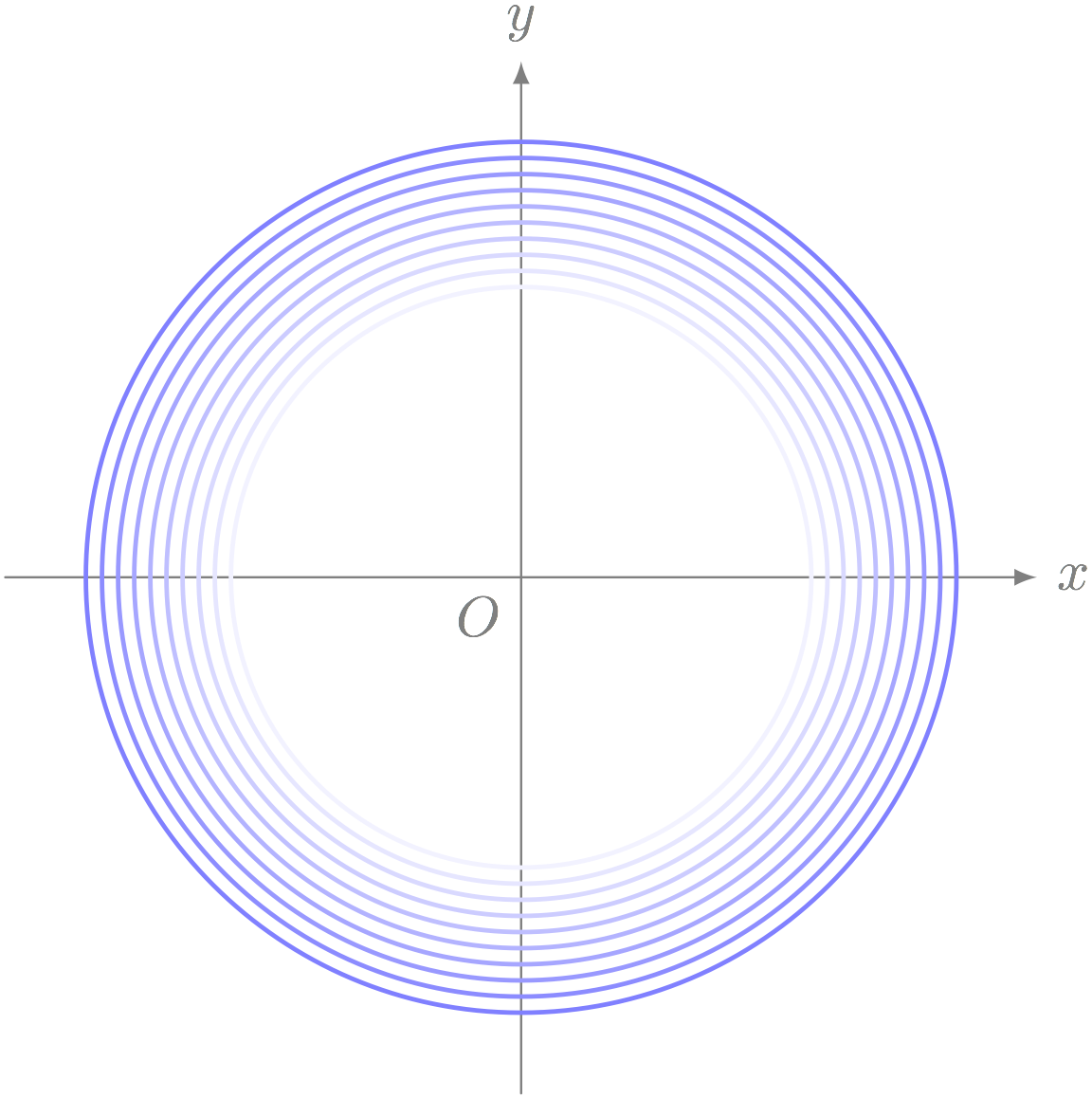
僕「逆に $r$ がどんどん小さくなって……ゼロに近づけば近づくほど、 $x^2+y^2=r^2$ という方程式が表す円は小さくなる」

ユーリ「……」

僕「ん？　何かおかしい？　そんなに難しい話はしてないよね？」

ユーリ「ねーお兄ちゃん。 $r=0$ になったらどーなるの？」

僕「$r=0$ になったら一点になるから、ふつうは円とは呼べないね。まあ半径がゼロの円と言ってもいいけど」

ユーリ「なに急に顔赤くしてんの？」

僕「赤くなんかしてないよ。 $x^2+y^2=0^2$ を満たすような点 $(x,y)$ は、 $(0,0)$ しかない。だからこの方程式を満たす点は原点の一点だけだよ」

ユーリ「そっから先は？」

僕「先って？」

ユーリ「$r$ を小さくして、ゼロの先。マイナスになったらどーなるの？」

僕「マイナス！　半径は長さだからマイナスにはならないね」

ユーリ「でも、 $x^2+y^2=r^2$ だったら、 $r$ は二乗してるじゃん？　だったら、 $r$ がマイナスでも大丈夫だよ」

僕「うん、それはそうだなあ。もしも $r<0$ だとしたら、 $x^2+y^2=r^2$ が表している図形は、 原点が中心で半径が $|r|$ になる円と呼べるね。 半径が $r$ の絶対値ということ」

ユーリ「ふんふん。 $r$ がすごくマイナスになったら、すごく大きな円になるわけ？」

僕「そうなるね」

文字が表しているもの

僕「だから、円の方程式 $x^2+y^2=r^2$ を見たときには、 $r\geqq 0$ だったら $r$ は円の半径を表しているといえるけど、 $r<0$ だったら、 $r$ は円の半径を表しているとはいえない」

ユーリ「ふんふん」

僕「数式を見たときには、そこに出てくる文字が何を表しているかをちゃんと 確かめておかないといけないよ」

ユーリ「おー、ひさびさの教師トーク！」

僕「なんだそれ」

ユーリ「$r$ は、まあいーんだけど、 $x$ と $y$ は何を表してるの？　これも文字でしょ？」

僕「$x$ は点の $x$ 座標で、 $y$ は点の $y$ 座標だよ。 もう少しちゃんといえば、 $x^2+y^2=r^2$ が表している円の、 円周上にある点の座標 $(x,y)$ を表している」

ユーリ「お兄ちゃん、そーゆーの、練習してんの？」

僕「そういうのって何のこと？」

ユーリ「円の半径とか点の座標とか、さくさくさくって答えるじゃん。 劇の台本読むみたいに練習してんの？」

僕「そんなことないけど、数学の本読んだり、問題を解いたりするときに、 心の中で毎回確かめているからじゃないかな。 『この式の $r$ って何だっけ』とか『ここでは $x$ は何を表しているかな』みたいに、 自分で確かめながら本を読んでいる。だから、さっと言えるんだと思うよ」

ユーリ「へー」

円を動かす

僕「そうだ。さっきは半径 $r$ を変えて、円を大きくしたり小さくしたりしたよね」

ユーリ「そーだね」

僕「今度は横に動かしてみよう。ほら、ユーリのゲームでも、 大きな丸いのが動いてた。円を右に動かしてみよう」

ユーリ「ほほー」

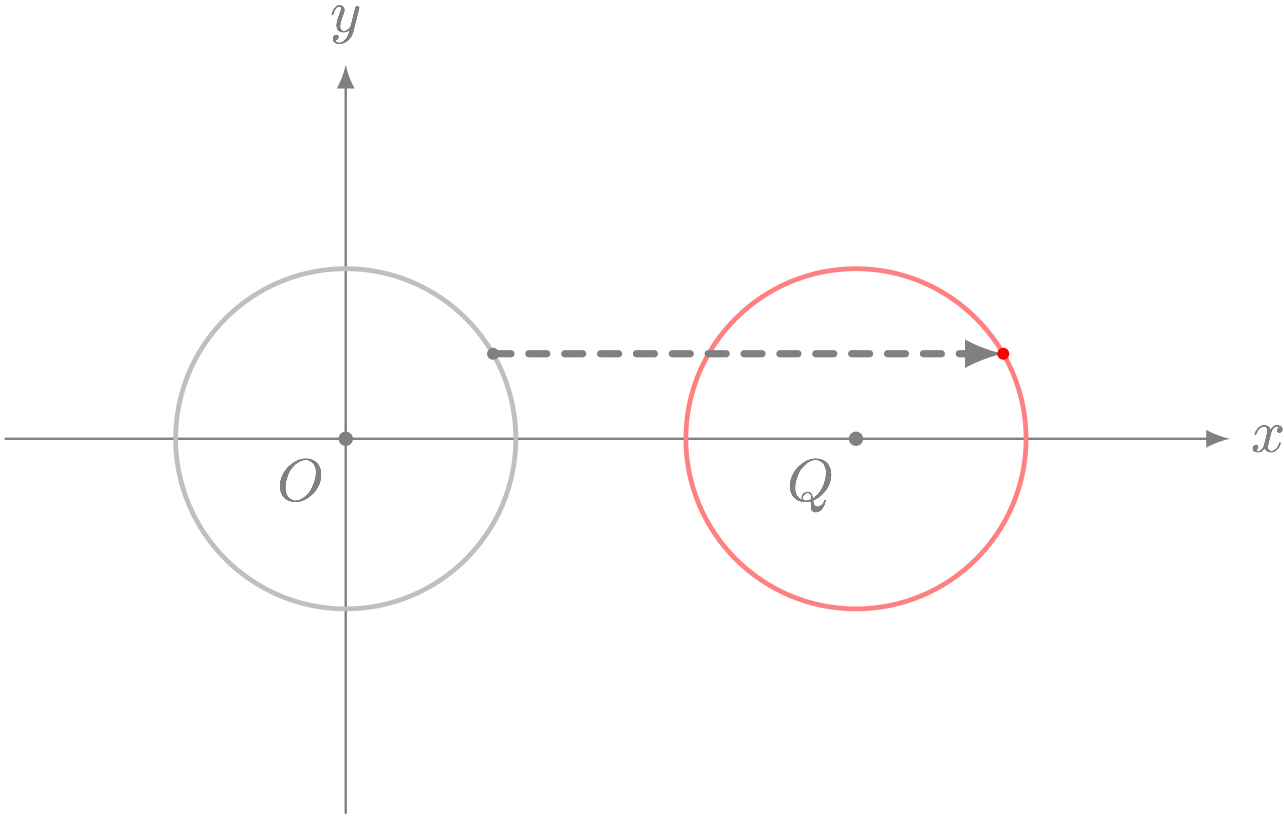
僕「どう？」

ユーリ「この問題って円 $O$ を $3$ だけ動かすってことでしょ。 だったら、 $x$ に $3$ を足せばいーんじゃないの？」

僕「そうなんだけど、そこをきちんと答えるのが大事。 円 $O$ を動かしてできる円 $Q$ の方程式はどうなる？」

ユーリ「だから、 $x+3$ にすればいい」

僕「……」

ユーリ「$(x+3{)}^2+y^2=r^2$ じゃないの？」

僕「違うんだよ、ユーリ」

ユーリ「違うの？」

僕「違うんだ。 $(x+3{)}^2+y^2=r^2$ だと、 円は $3$ だけ左に移動してしまう。 期待した動きとは逆になってしまうんだ」

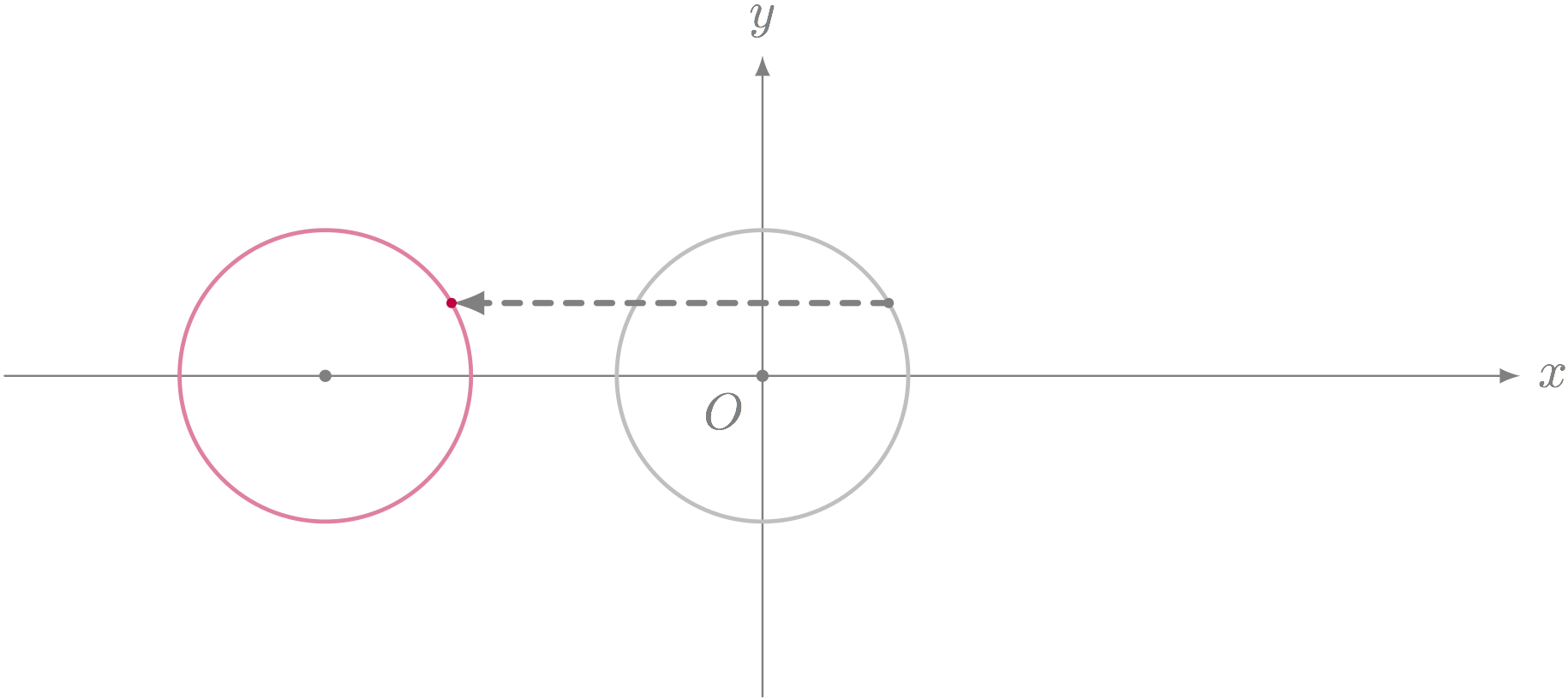
ユーリ「でもね、お兄ちゃん。 点 $(x,y)$ を右に $3$ 動かした点は $(x+3,y)$ でしょ？」

僕「その通りだよ。ユーリ、それは正しい」

ユーリ「ねーお兄ちゃん。何か気分悪い」

僕「どうした？」

ユーリ「何だかお兄ちゃん、ユーリがまちがっているの楽しそうなんだもん」

僕「違う違う。お兄ちゃんはユーリがまちがうのを楽しんでいるんじゃない。 お兄ちゃんも、ユーリと同じまちがいをしたの、思い出したからなんだ」

ユーリ「へー？」

僕「点 $(x,y)$ を右に $3$ 動かした点は $(x+3,y)$ になる。これは正しい」

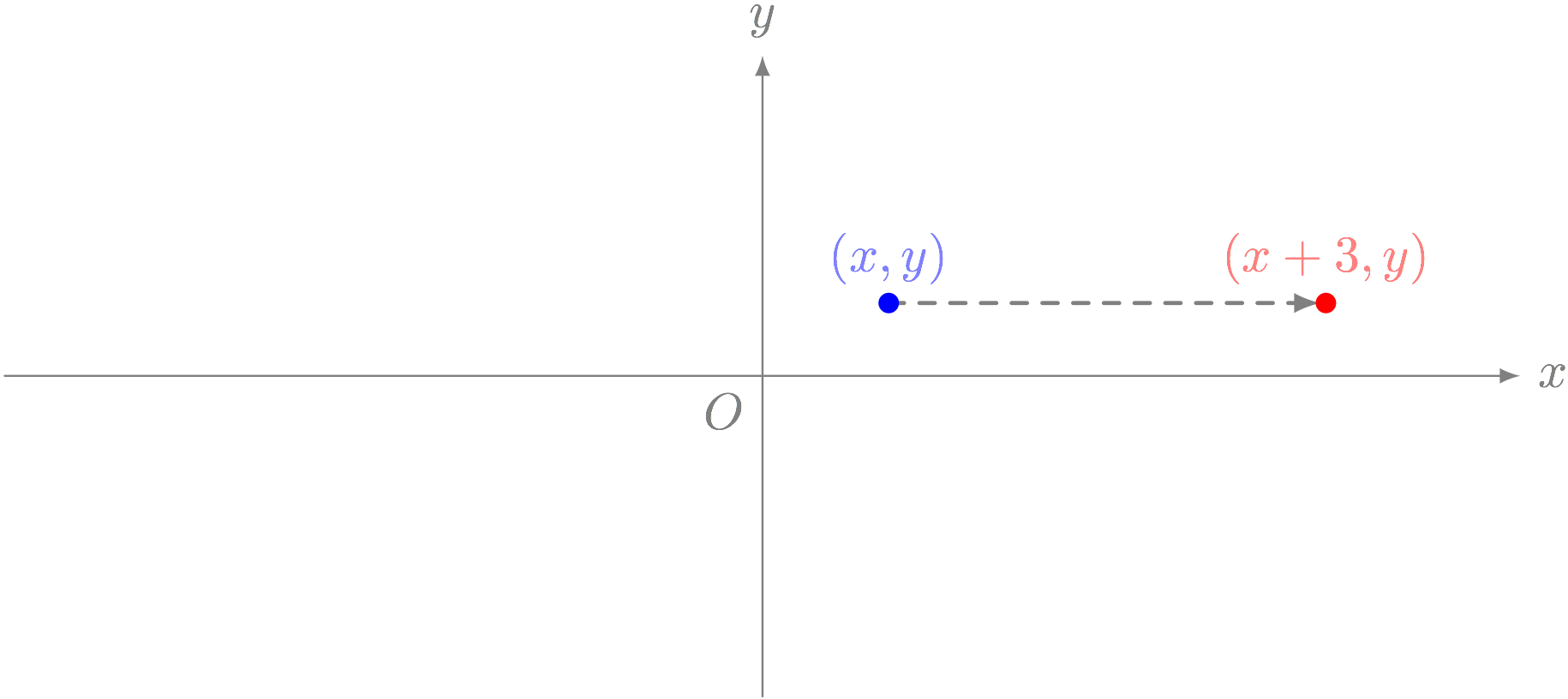
ユーリ「うん」

僕「でも、円 $x^2+y^2=r^2$ を右に $3$ 動かした円の方程式は、 $(x+3{)}^2+y^2=r^2$ じゃなくて、 $(x-3{)}^2+y^2=r^2$ なんだ」

ユーリ「うわー、納得できなーい」