![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
高校生の僕と中学生のユーリは、 不等式が表す領域についておしゃべりをしていた。 ちょうどいま、不等式 $y > \dfrac{1}{x}$ を満たす領域について答えが出たところ(第95回参照)。
解答4
不等式 $y > \dfrac{1}{x}$ を満たす領域は以下の通り(境界は含まない)。
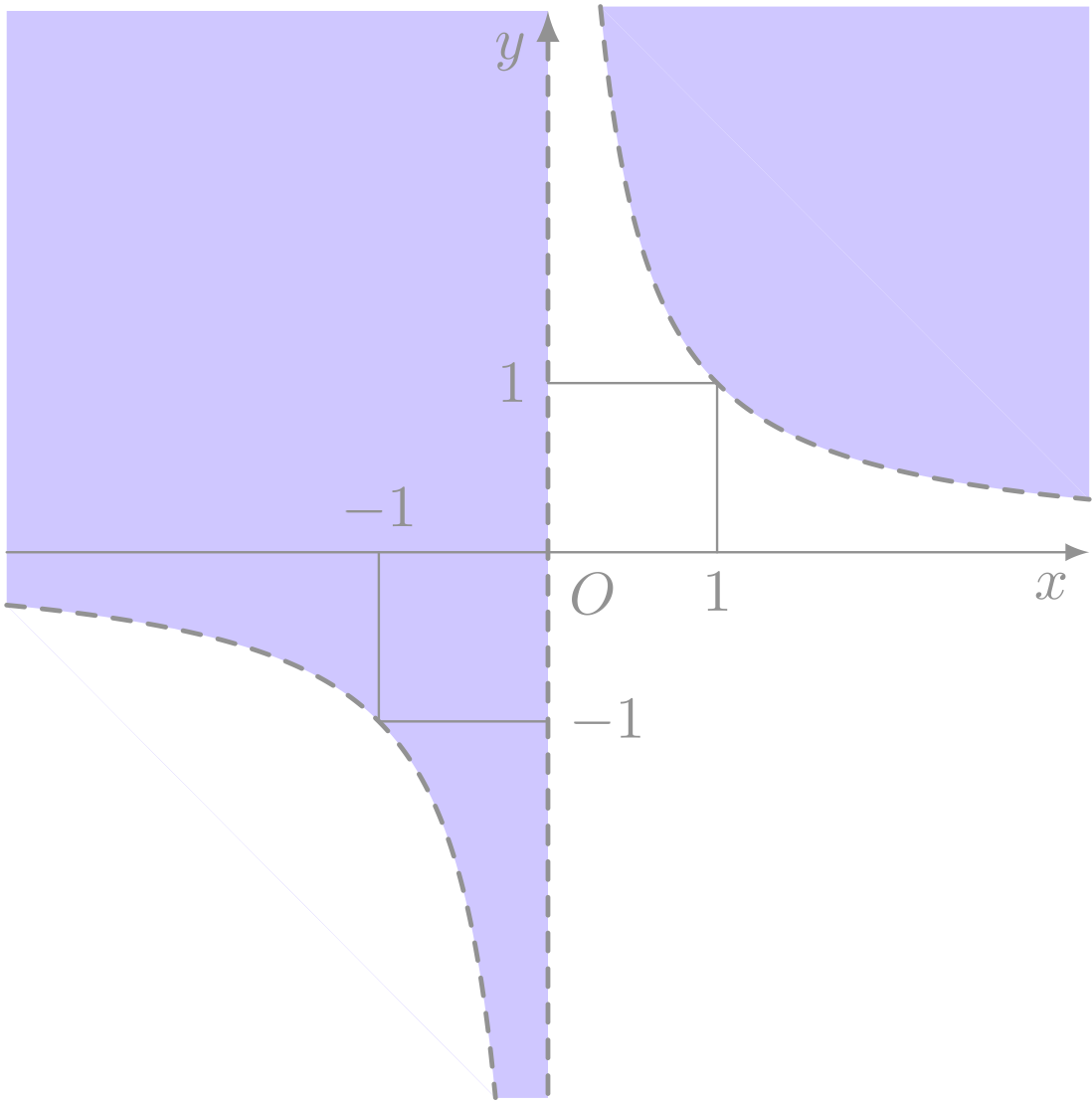
僕「では、これを踏まえて」
ユーリ「踏まえて?」
僕「この問題はわかる?」
問題5(双曲線と不等式)
次の不等式を満たす領域を図示せよ。
$$ xy > 1 $$
ユーリ「むむ? ……これって同じじゃないの?」
僕「同じって?」
ユーリ「ほら、その顔だよ!」
僕「??」
ユーリ「『引っかかったな』みたいな顔。そーゆーの、やな感じ」
僕「ごめんごめん。そういうつもりはないんだけどね。……同じって?」
ユーリ「$y > \dfrac{1}{x}$ の範囲は描いたじゃん? $xy > 1$ も同じじゃない?」
僕「どうしてそう思ったの?」
ユーリ「ゼロ割り関係ないから」
僕「? ユーリ……話、飛んでない?」
ユーリ「だってね、 $y > \dfrac{1}{x}$ のときって、 $x \NEQ 0$ じゃん? 分数出てきてるから」
僕「そうだね。確かにここでは $x \NEQ 0$ だよ」
ユーリ「そんで、それを踏まえて $xy > 1$ を考えるってことは、ゼロに注意するんでしょ? 分数なくなってるもん。 でもね、 $x = 0$ のときって、 $xy > 1$ は満たさないから関係ない。 だから、結局、 $y > \dfrac{1}{x}$ と $xy > 1$ は同じ」
僕「なるほど。よくわかったよ。ユーリはなかなか鋭いな。 ユーリの言う通り、『分数が出てきたらゼロ割りに注意』というのは正しいよ。 $y > \dfrac{1}{x}$ という式があったら、暗黙のうちに $x \NEQ 0$ が仮定されてる」
ユーリ「アンモクのウチ?」
僕「式として $x \NEQ 0$ が書かれていなくても、という意味。 $\dfrac{1}{x}$ のような分数が出てきたら、すぐそばに 『ただし、 $x \NEQ 0$ である』という条件が添えてあると考えなくちゃいけない。 でも $xy > 1$ には分数は出てきてないから、そんな条件は付いてない」
ユーリ「そー! だから、おんなじ」
僕「等式だったらそれでいいんだけど、これは不等式だから……」
ユーリ「あーっと! マイナスは逆かあ!」
僕「わかった?」
ユーリ「$x$ がプラスのときは、 $xy > 1$ は $y > \dfrac{1}{x}$ と同じだけど、 $x$ がマイナスのときは、 $y < \dfrac{1}{x}$ と同じだね。逆だった!」
僕「そうそう。そうなるね。 $x$ がマイナス、つまり $x < 0$ のときは、 $xy > 1$ の両辺を $x$ で割ると不等号の向きが反転して $y < \dfrac{1}{x}$ になる。とても間違いやすいところだね」
ユーリ「じゃあ、 $xy > 1$ はこーなるの?」
解答5(双曲線と不等式)
不等式 $xy > 1$ を満たす領域は以下の通り(境界は含まない)。
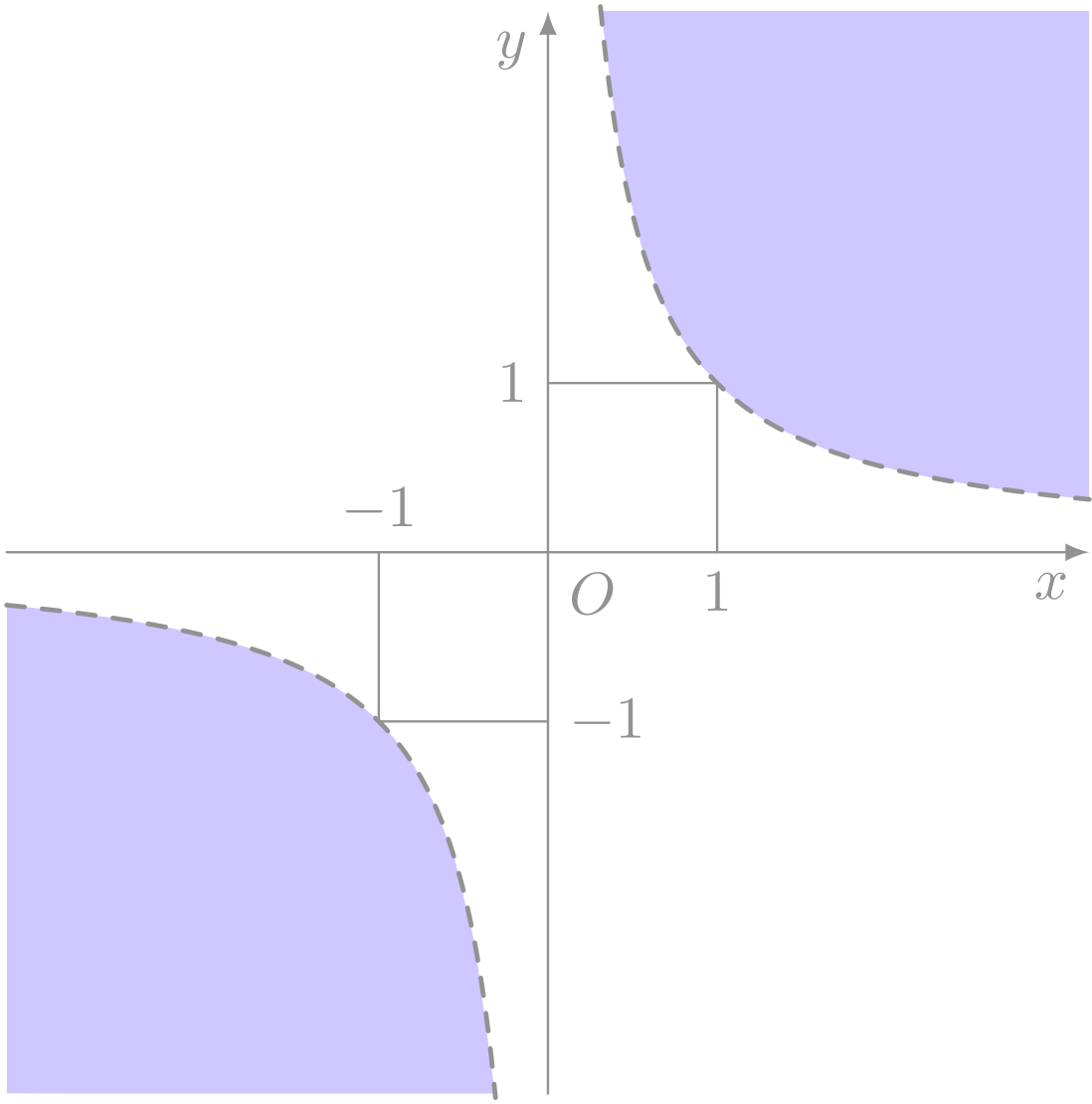
僕「そうだね、それで正解」
ユーリ「やたっ!」
僕「$xy > 1$ の領域を求めるのに、 $x$ の正負について《場合分け》をして考えたことになるね。 $x > 0$ か、 $x = 0$ か、 $x < 0$ かという場合分け」
$x$ の正負について場合分け
ユーリ「うん。これってあたりまえだよ。だって、 $x$ と $y$ がマイナスですごく小さいとき、 $xy$ はすごく大きくなるでしょ? $x = -100$ と $y = -100$ だったら、 $xy = 10000$ で、 $1$ よりもずっと大きくなる。だから、左下の方はずっと $xy > 1$ になってるはず」
僕「そう! それはとてもいい確かめ方だね!」
ユーリ「ねーお兄ちゃん。逆にして、 $xy < 1$ の領域って、内側?」
僕「内側だよ。そして $xy < 1$ だと、ゼロ割りの心配がないから、 $y$ 軸もちゃんと含む」
ユーリ「にゃるほど」
$xy < 1$ の領域

僕「実数 $x$ が出てきたら、 $x > 0$ と $x = 0$ と $x < 0$ で場合分けをするというのは、 よくあることだよ」
ユーリ「プラスと、ゼロと、マイナス」
僕「そうそう。実数は必ずその三種類のどれかになるから、 $x > 0$ と $x = 0$ と $x < 0$ で場合分けをすれば漏れがないんだ」
ユーリ「ふんふん。バシッと決まる」
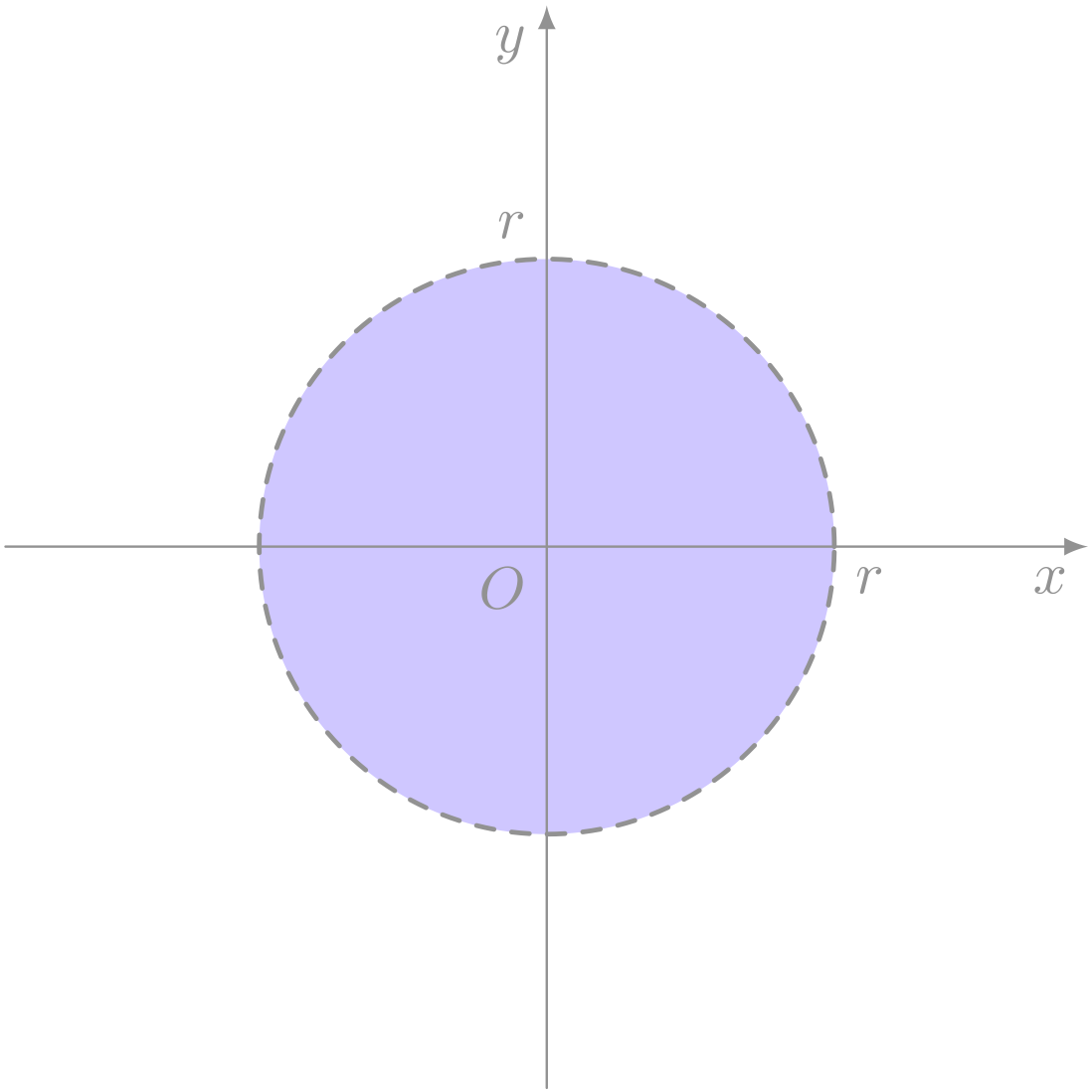
僕「さっき描いた円の領域でも、 似たような話がいえる(第95回参照)。 座標平面上のどんな点でも必ず、 《円の外部》と《円周上》と《円の内部》の三種類のどこかになるよね」
ユーリ「そりゃそーだね。逃れられない」
僕「$x^2 + y^2 = r^2$ という円を考えると……」
円を使った、座標平面上にある点の場合分け
$$ \left\{\begin{array}{llll} x^2 + y^2 &> r^2 && \REMTEXT{円の外部} \\ x^2 + y^2 &= r^2 && \REMTEXT{円周上} \\ x^2 + y^2 &< r^2 && \REMTEXT{円の内部} \\ \end{array}\right. $$
円の外部 $x^2 + y^2 > r^2$
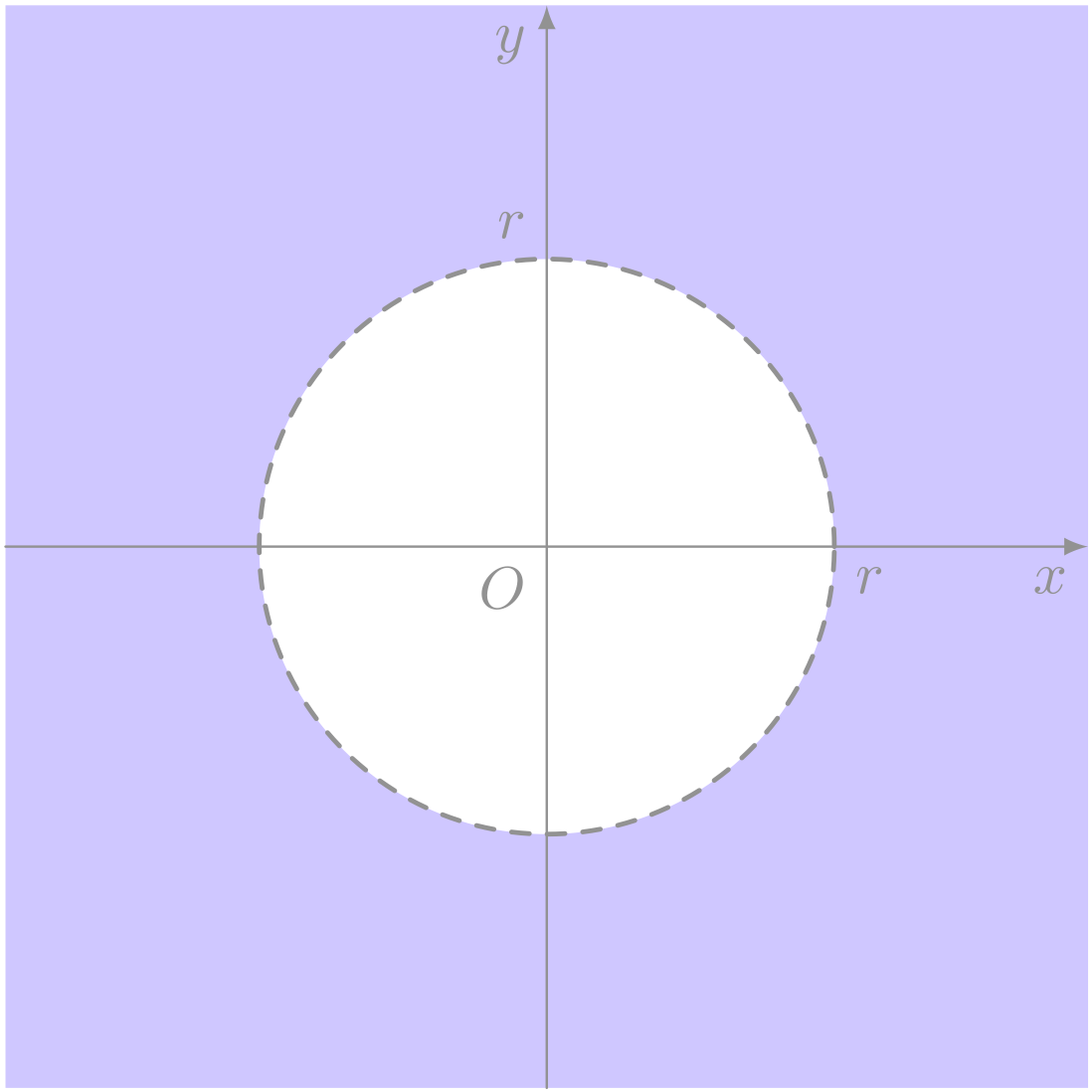
円周上 $x^2 + y^2 = r^2$
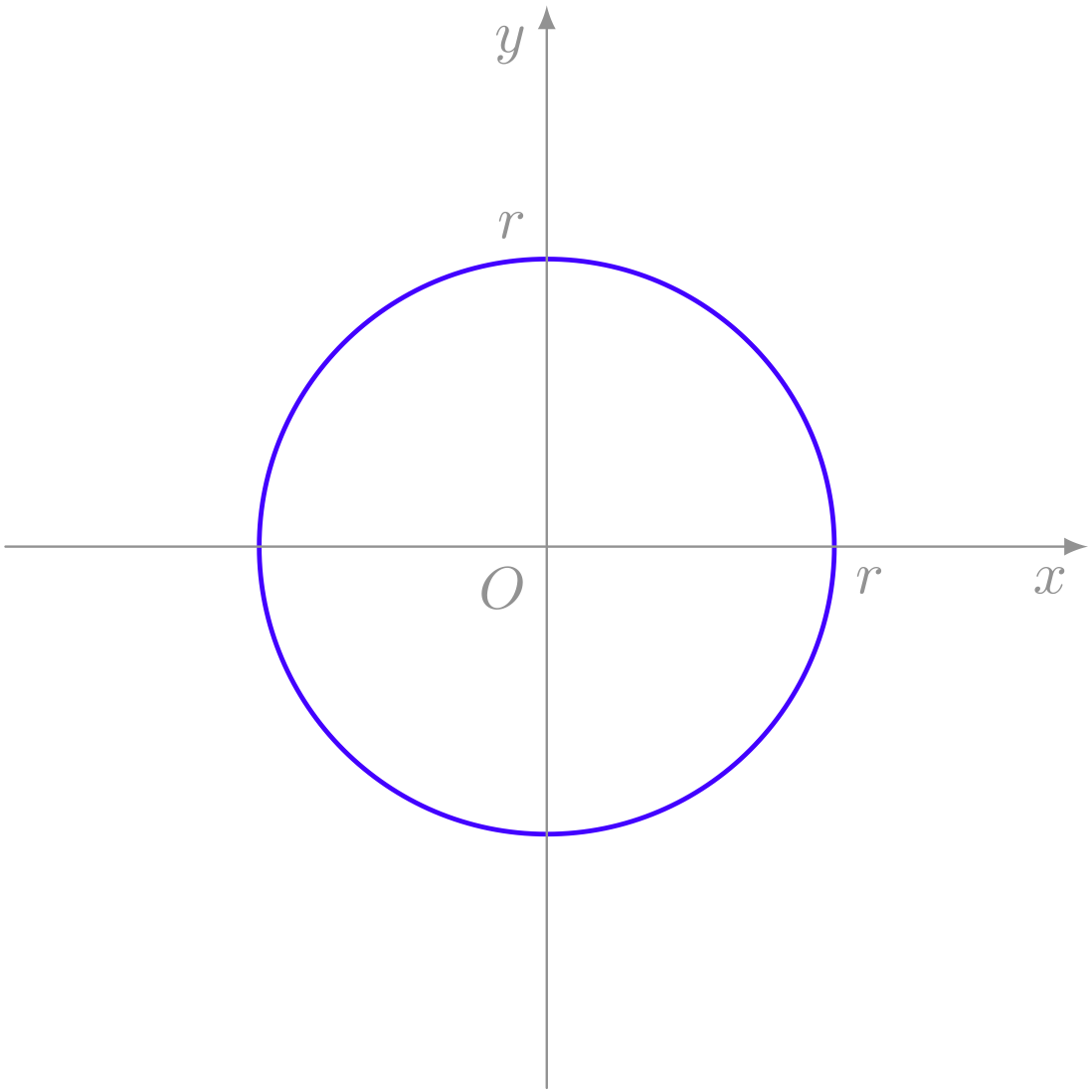
円の内部 $x^2 + y^2 < r^2$
僕「そうだ、おもしろい問題を思いついたぞ。ユーリが好きそうな話」
ユーリ「なになに?」
僕「こういうのはどうだろう」
問題6
$x,y$ は実数、 $r$ は $0$ 以上の実数とする。このとき、
「$x^2 + y^2 < r^2$ ならば、 $-r < x < r$ である」
という主張はいつも正しいか。
ユーリ「おお?」
僕「これはね」
ユーリ「待ってよ! 考えるから!」
そういって、ユーリは深い思考に入った。
ユーリの栗色の髪が金色に輝いて見える。
(あなたも、考えてみてください)

僕「どうかな?」
ユーリ「わかった! 正しい!」
僕「そう? どうしてそういえる?」
ユーリ「この問題って、 《$x^2 + y^2 < r^2$ ならば、 $-r < x < r$》 をいうんでしょ?」
僕「そうだね、もしもこの主張が正しいなら」
ユーリ「うん、正しいもん。何でかっていうとね、 $x$ はそんなに大きくも小さくもなれないから」
僕「ほう?」
ユーリ「$y^2$ って必ず $0$ 以上じゃん? そして、 $x^2 + y^2 < r^2$ だったら、 $x^2$ に $0$ 以上の数を足したのに、 まだ $r^2$ より小さいってこと。だから、 $x$ は $-r$ から $r$ の間に入ってなきゃだめだもん」
僕「うん、いいね。考え方はそれでとてもいい」
ユーリ「なんか引っかかる言い方」
僕「考え方はいいけど、それでユーリが好きな《バシッと決まる》感じがするかな」
ユーリ「答え方が悪いってこと?」
僕「ユーリの答えを順序立てて述べればいいだけだよ」
$x^2 + y^2 < r^2$ ならば、 $x^2 < r^2$ がいえる。
なぜなら、 $x^2 \LEQ x^2 + y^2$ で、 $x^2 + y^2 < r^2$ だから。
ユーリ「ふんふん」
そして、 $x^2 < r^2$ ならば、 $-r < x < r$ がいえる。
なぜなら、 $x^2 < r^2$ から、 $\ABS{x} < \ABS{r}$ がいえて、 これは $-r < x < r$ に他ならない。
ユーリ「ユーリの答えと同じに見える……」
僕「でね、ここで領域を描いてみよう!」
ユーリ「へ?」
僕「つまり、こういう問題」
問題7(不等式と領域)
$x,y$ は実数、 $r$ は $0$ 以上の実数とする。 このとき、以下の領域 $A$ と領域 $B$ を描け。
(領域 $A$)$x^2 + y^2 < r^2$
(領域 $B$)$-r < x < r$
ユーリ「領域 $A$ は……円の内部だよね」
僕「そう。原点中心で半径 $r$ の円の内部だね」
ユーリ「領域 $B$ は、 $-r$ から $r$ まで?」
僕「まあまあ、図を描こうよ」
解答7(不等式と領域) $x,y$ は実数、 $r$ は $0$ 以上の実数とする。 このとき、
(領域 $A$)$x^2 + y^2 < r^2$
(領域 $B$)$-r < x < r$
の二つの領域は以下の通り。

領域 $A$ は円の内部で、領域 $B$ は斜線を引いた帯の内部になる。
ユーリ「それで? これが?」
僕「この図をよく見ると、領域 $A$ は、領域 $B$ にすべて含まれていることがわかるよね?」
ユーリ「そーだね。円の内部は帯の中に入ってるってことでしょ?」
僕「ということはだ、領域 $A$ に入っているどんな点 $(x,y)$ を選んだとしても、 その点は領域 $B$ にも入っているといえるわけだ。これで問題6の主張が正しいといえた」
ユーリ「なーるほど!」
僕「わかる?」
ユーリ「わかるわかる! 『$x^2 + y^2 < r^2$ ならば $-r < x < r$ である』といえるんでしょ?」
僕「そうだね。 《不等式を使った論理の問題》が、 《領域を使った幾何の問題》に移されているんだよ」
解答6
$x,y$ は実数、 $r$ は $0$ 以上の実数とする。このとき、
「$x^2 + y^2 < r^2$ ならば、 $-r < x < r$ である」
という主張はいつも正しいといえる。
なぜなら、点が領域 $A$(円の内部)の中にあるならば、その点は領域 $B$ の中(帯の内部)にあるから。

ユーリ「なーるほど。あっ、だったらさー、同じことを $y$ でもいえるよね」
僕「いえるね。《$x^2 + y^2 < r^2$ ならば、 $-r < y < r$ である》といえる」
ユーリ「うんうん。……ねー、お兄ちゃん。これって、反対にしてもいいの?」
僕「反対って?」
ユーリ「てきとーに図を描いて、不等式を使った論理の問題にしちゃうの」
僕「ああ、いいね。 たとえば、こういう図からは、どんな問題が作れると思う?」

無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2014年11月14日)