![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
早くも書籍化第四弾!
『数学ガールの秘密ノート/数列の広場』はこちら!
ここは僕の高校。 放課後、図書室に入ったとたん、僕はテトラちゃんに腕をつかまれた。
僕「うわっ! テトラちゃん……どうしたの?」
テトラ「先輩先輩! お待ちしておりました。どうぞこちらへ」
テトラちゃんはそう言って、僕を机まで引っ張っていった。
僕「うれしそうだね」
テトラ「はいっ! 実はですね、村木先生からの《研究課題》を一つ解いたんです!」
僕「あ、そうなんだ。今回は、どんなカード?」
テトラ「これです!」
村木先生のカード

僕「《正方形の方程式》……村木先生の今回のカードはこの一言なんだね」
村木先生は、僕の高校の数学教師。 ときどき、数学の問題を考えるための《カード》を僕たちにくれる。 数学の問題が直接書かれているときもあるけれど、 数式が一つだけぽつんと書かれているときもある。 その数式をきっかけとして、僕たちは自由に数学を考えるのだ。
テトラ「はい、そうです。 先日、ジグザグのグラフを描いたじゃないですか(第81回参照)(第82回参照)」
僕「うん」
テトラ「あのとき、たくさんの数式ができたので、自主レポートにして村木先生に持っていったんです」
僕「なるほど。まとめたんだね」
テトラ「そうしたら先生はこのカードをくださって……で、 あたしはこの問題を解いてたんです」
僕「それで、解けたと」
テトラ「はい! 先輩、聞いていただけますか? テトラの解説。 今日はいつものテトラではありません!」
僕「もちろん!」
こうして、テトラちゃんの解説が始まった。
テトラ「まずですね、このカードには問題が書かれていません。 ただ《正方形の方程式》と書かれているだけですから。 あたしは、こんな問題を解いてみようと思いました」
問題1(正方形の方程式)
正方形を描く方程式を求めてください。
僕「ふむふむ?」
テトラ「放物線を描く方程式や、円を描く方程式がありますし、 このあいだのようにジグザグな線を描く方程式だってあるんですから、 《正方形を描く方程式》もあるはずだと思ったんです」
僕「うん、いいよ」
テトラ「考え始めてすぐ、 あたしは先輩がよくおっしゃる《ポリアさんの問いかけ》を思い出しました。 問いかけ上手なポリアさんの《図をかけ》です」
僕「《図をかけ》……いいねえ」
ポリアの問いかけ
《図を書け》
テトラ「あたしは正方形のことをよく知っている、と、思っていますけど、 念のため、図を描こうとして、気付きました」
僕「何を?」
テトラ「《正方形を描く方程式》といっても、 ひとつには決まらないってことです! 座標平面のどこに、 どういう向きで、どういう大きさの正方形を描くかで、方程式は変わりますから!」
どんな正方形を描くつもり?
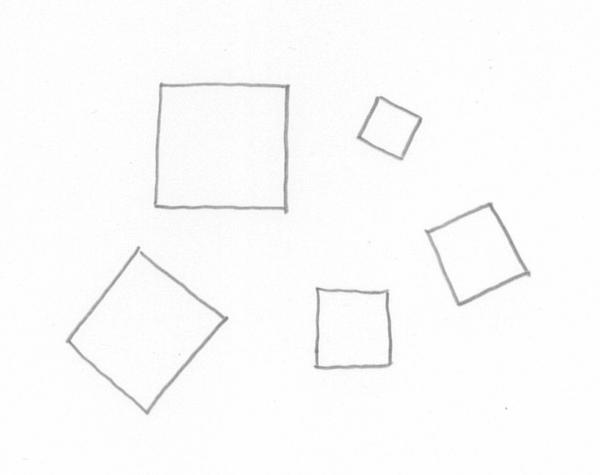
僕「確かにね」
テトラ「つまり、問題の立て方によって答えは変わるということですっ! ……あ、 あたりまえですけれど。そこでまた《ポリアさんの問いかけ》が思い浮かびました。 今度は《似ているものを知らないか》です」
ポリアの問いかけ
《似ているものを知らないか》
僕「ふむふむ」
テトラ「あたしが村木先生からカードをもらったのは、 ジグザグ線のレポートを持っていったときでした。 そこで気付いたんですが、ジグザグ線に似た、 こういう正方形を描く方程式を見つけることにすればいい、 と思いました」
問題1a(正方形の方程式)
次の正方形を描く方程式を求めてください。
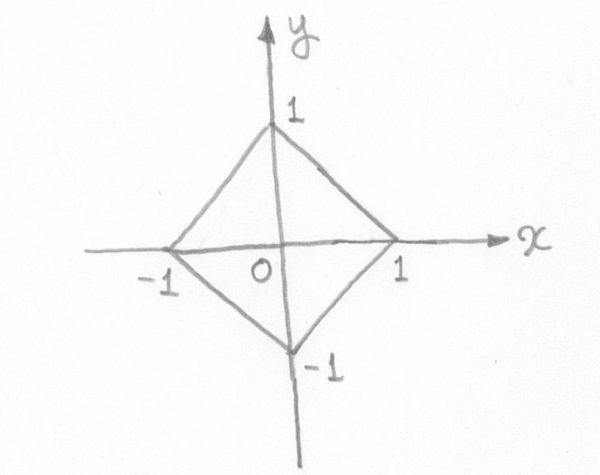
読者さんへ
ここで先に進むのをちょっとだけストップして、 テトラちゃんの問題を考えてみましょう。
あなたなら、どう考えますか?
僕「うまい! なるほどね。ジグザグの線を使えるんじゃないかと思ったんだね」
テトラ「そうです! 斜めに置いたこの正方形は、四本の直線でできています。 こんな直線です」
$$ \left\{\begin{array}{llll} y &= -x + 1 && \REMTEXT{(1)} \\ y &= x + 1 && \REMTEXT{(2)} \\ y &= -x - 1 && \REMTEXT{(3)} \\ y &= x - 1 && \REMTEXT{(4)} \\ \end{array}\right. $$

僕「直線というか、線分だよね。長さが限られているから」
テトラ「あ、先輩! 言っちゃだめですよう。 テトラはちゃんとそれに気付きましたよ。 $x$ の範囲を考えればいいんです」
$$ \left\{\begin{array}{llll} y &= -x + 1 && (0 \leqq x \leqq 1) \cdots\REMTEXT{(1)} \\ y &= x + 1 && (-1 \leqq x \leqq 0) \cdots\REMTEXT{(2)} \\ y &= -x - 1 && (-1 \leqq x \leqq 0) \cdots\REMTEXT{(3)} \\ y &= x - 1 && (0 \leqq x \leqq 1) \cdots\REMTEXT{(4)} \\ \end{array}\right. $$
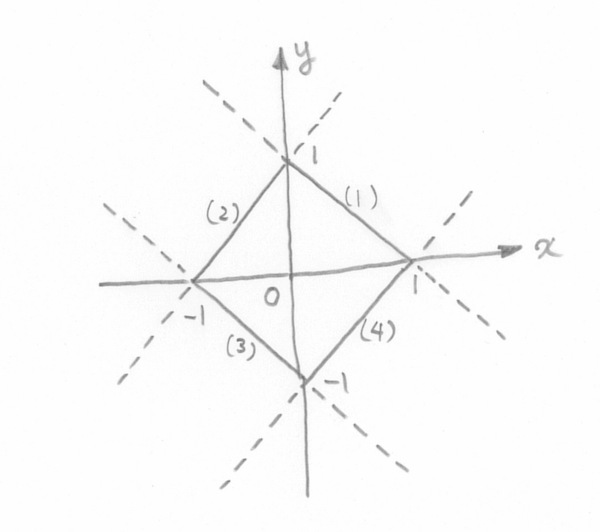
テトラ「はい、これで一応は問題が解けたことになります。 正方形の方程式ができましたから。 でも、これでは四本の式が必要になります。 ですから、あたしは、これを一本の式にできないかな、と思いました」
僕「そうだね。式が四本でも数学的にはまったく問題ないけど、 もっと簡単に書きたくなるよね」
テトラ「はい、そうです。それでですね、 あたしはその解決方法を知っています。 ジグザグ線を描くときに、絶対値を使いましたから!」
僕「似てるものを知っているわけだね」
テトラ「上の二辺が作る《山》はこうです。これは $(1)$ と $(2)$ の辺を合わせたものです」
正方形の《山》を描く方程式
$$ \begin{align*} y &= -\ABS{x} + 1 && (-1 \leqq x \leqq 1) \\ \end{align*} $$
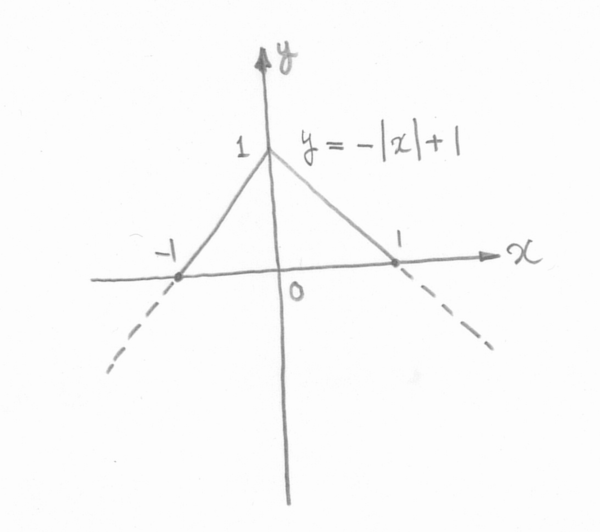
僕「……」
テトラ「そして、下の二辺が作る《谷》はこうなります。こちらは $(3)$ と $(4)$ の辺を合わせました」
正方形の《谷》を描く方程式
$$ \begin{align*} y &= \ABS{x} - 1 && (-1 \leqq x \leqq 1) \\ \end{align*} $$

僕「……」
テトラ「これで、四本だった式が $y = -\ABS{x} + 1$ と $y = \ABS{x} - 1$ の二本になりました! あたしは次に、この二本もまとめられないかって考えたんです! すごく時間が掛かりましたけど、あたしは、《谷》を上下ひっくり返すと《山》に なることに気付きました! つまり、こういうことです」
《谷》を上下ひっくり返すと《山》になる
$$ -(\underbrace{\ABS{x} - 1}_{\REMTEXT{《谷》}}) = \underbrace{-\ABS{x} + 1}_{\REMTEXT{《山》}} $$
僕「まあ、そうだね」
テトラ「? ……そ、それでですね、あたしの解答はこうなりました!」
解答1a(テトラちゃんの解答)
$$ y = \pm (\ABS{x} - 1) \qquad (-1 \leqq x \leqq 1) $$

僕「なるほど、そうなるね」
テトラ「先輩……あたし、何かまちがってました?」
僕「いや、これは正しいよ。テトラちゃんの解答はちゃんとこの正方形を描く方程式になってる」
テトラ「でも、あの……先輩は納得なさっていないようなので」
僕「ごめんごめん。ちょっと別のことを考えていたんだ。 テトラちゃんは関数の考え方でこの問題を解いたんだね」
テトラ「はい?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2014年9月5日)