![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
テトラちゃんは僕の一年後輩。 いつも元気で熱心に数学を勉強している。 今日も僕たちは放課後の図書室で数学トークを繰り広げる。
テトラ「それにしても不思議です」
僕「何が?」
テトラ「これ、先日の《数学基礎力確認テスト》の問題なんですが」
問題1
以下のグラフを表す方程式を答えよ。
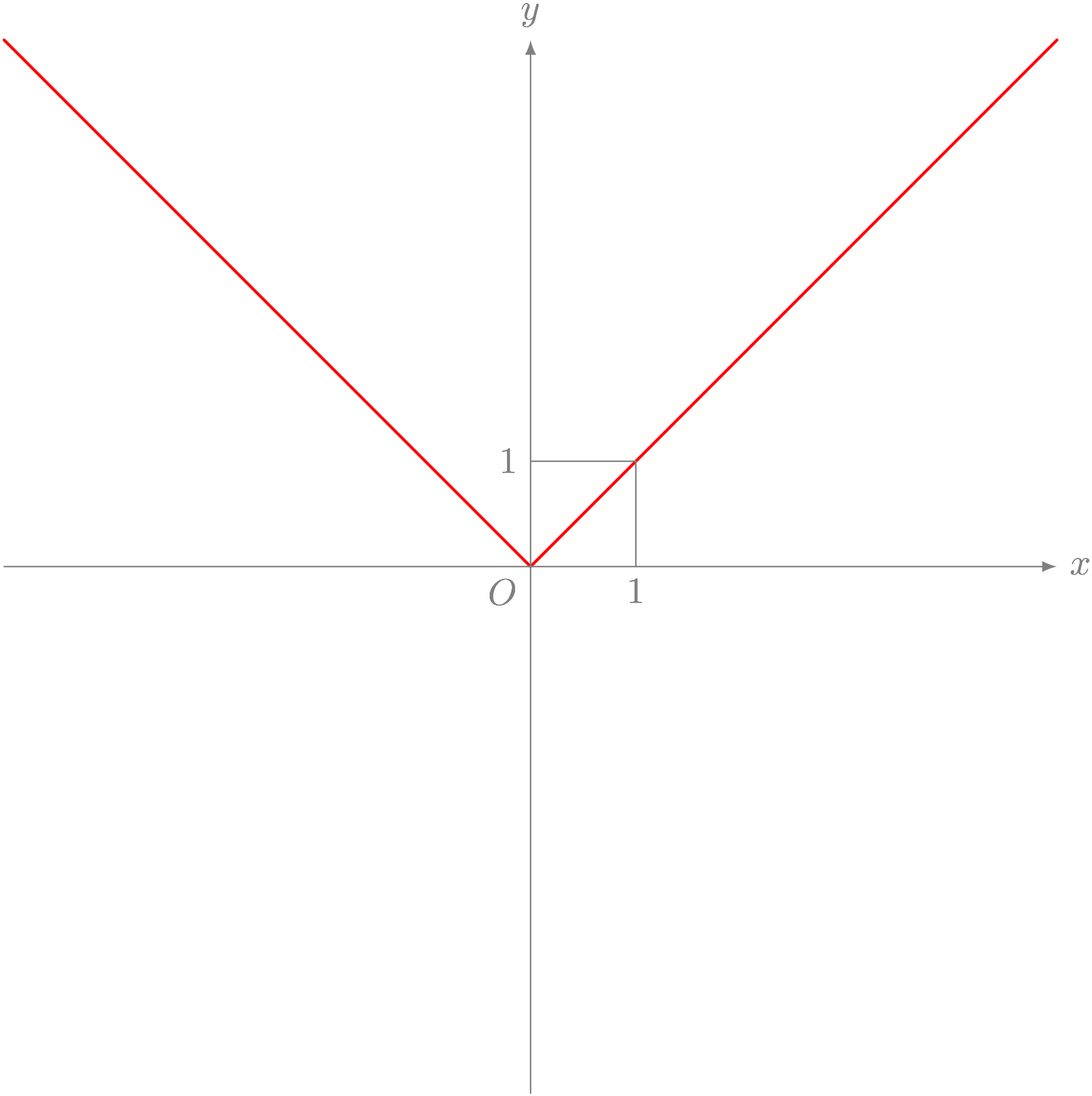
僕「そのテストって何?」
テトラ「はい、先日から教生の先生がいらしていて、みなさんの力を教えてくださいって……」
僕「へえ……それでこういうテストをしたの?」
テトラ「そうですけど……」
僕「テトラちゃんは、答えられたよね?」
テトラ「いえ、実は、その……いちおう答えたんですが……」
僕「これって絶対値でしょ? $y = \ABS{x}$ だよね」
解答1
$ y = \ABS{x} $

テトラ「ああ……やっぱり、そうお答えになりますよねえ……」
僕「うん、基本的な問題だよね。テトラちゃんの答えはどうだったの?」
テトラ「あたし、難しく考え過ぎちゃうんでしょうか。 こんな答えをしてしまいました。 $y = \sqrt{x^2}$ です」
テトラちゃんの解答1
$ y = \sqrt{x^2} $

僕「なるほど、 $y = \sqrt{x^2}$ か! 確かにこれでも立派な正解だね」
テトラ「そうなんでしょうか」
僕「もちろんだよ。教生の先生が期待した答えは絶対値を使った $y = \ABS{x}$ だと思うけど、 出された問題に対してはテトラちゃんの答えで何も恥ずかしくないよ。 むしろおもしろいかも」
テトラ「あ、あたし、そうは思えませんでした。 絶対値が答えだと聞いたとき、とてもショックでした。 絶対値のことは、以前先輩にていねいに教えていただいたのに、気付かなかったなんて……ほんとに不思議です」
僕「そういうことはあるよ。 ところでテトラちゃんはどうやって $y = \sqrt{x^2}$ という方程式を思いついたの? 僕はそっちの方が気になるんだけど」
テトラ「あ、あの……あたしは、先輩から教えていただいた《ポリアさんの問いかけ》を思い出したんです。 問いかけ上手なポリアさん」
僕「うんうん」
テトラ「あたしは、このグラフを見て《似ているものを知らないか》という問いかけをしてみました。 そして、 $y = x^2$ のグラフと似てる! って気付いたんです」
$y = \ABS{x}$ のグラフと $y = x^2$ のグラフ
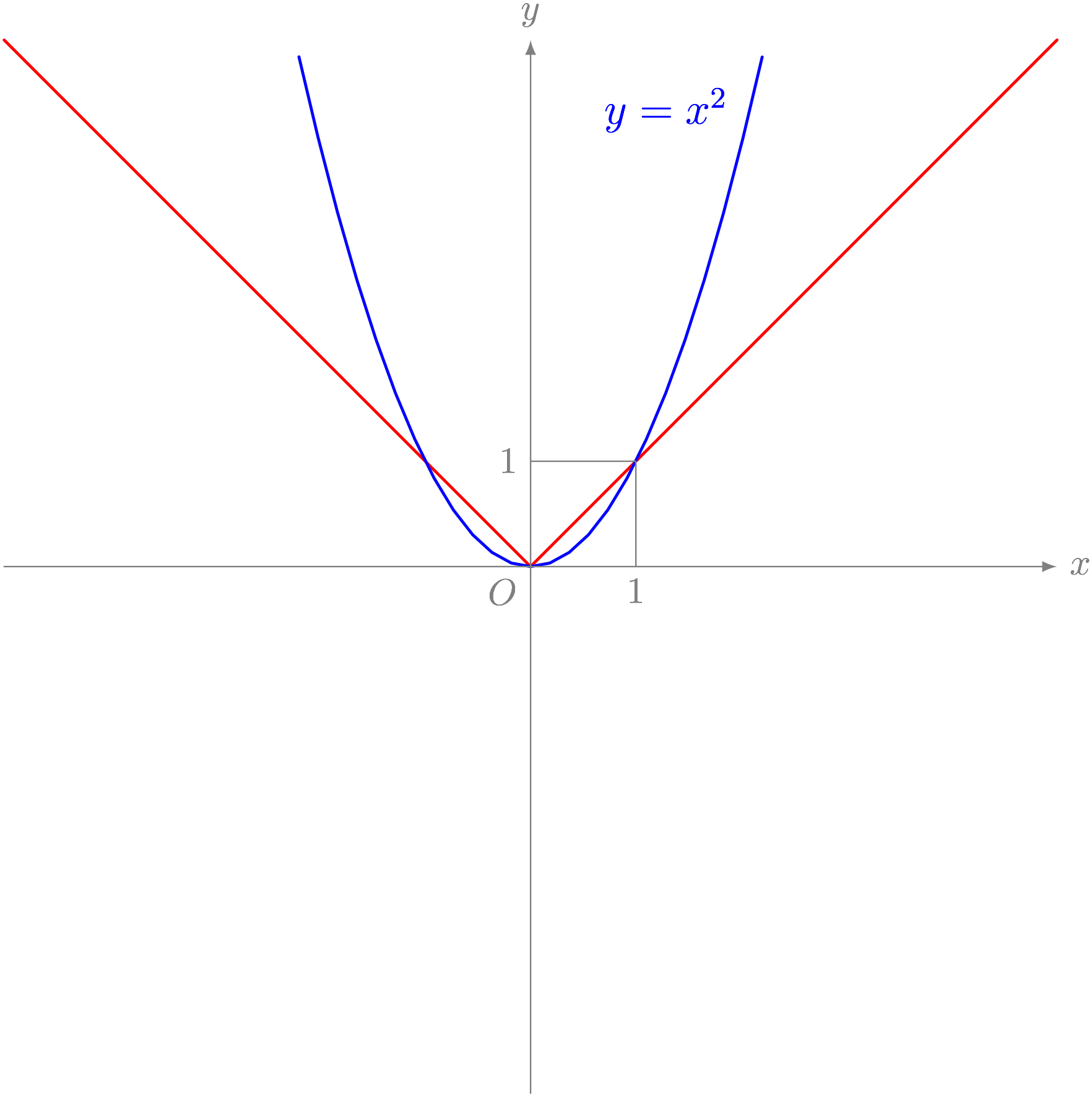
僕「なるほど、なるほど」
テトラ「だってそうですよね。どちらも原点に向かってすうううっと下がってきて、 原点からはすうううっと上がっていきます」
テトラちゃんは大きく手を動かしてグラフを描く。
僕「そうだね、その通り」
テトラ「この二つのグラフは似ています。ですから、 $y = x^2$ という方程式を少し変えればいいのでは、って思ったんです」
僕「いいねえ」
テトラ「$y = x^2$ のグラフはぎゅうんと曲がっています。これをまっすぐにしたいと思って、 そして、ええと、そもそもどうして曲がっているんだろうと思いました。 $x^2$ は $2$ 乗しているのでまっすぐじゃない。だったら戻してやればいい……そんなふうに考えました。 $2$ 乗を元に戻すにはルートを取ればいいですよね。それで $y = \sqrt{x^2}$ という式を作ったんです」
僕「すごいすごい」
テトラ「でも、それだけ考えたのに、絶対値を思い出せなかったということにショックを受けました……」
僕「まあ、それはそうなんだけど。テトラちゃんはちゃんとポリアの《似ているものを知らないか》を生かせたんだね。 それに、曲がったグラフをまっすぐにするために、 $2$ 乗したもののルートを取ったというのもすごいと思うよ。 だって、それは、自分の目的のために式変形を使いこなしたってことだからね」
テトラ「そ、それはそうですが……先輩ってすごいですね……あたし、なんだか、元気になります。 そうですよね、確かにあたしは数式の式変形を使って問題を解きました。 もっとも、あまり、そうは意識していなかったんですが」
僕「ついでに、もう少しこのグラフを観察して考えてみようか」
テトラ「はい?」
$y = \ABS{x}$ のグラフと $y = x^2$ のグラフ

僕「テトラちゃんは、絶対値のグラフがどうしてこんなふうに下がって、上がるか、説明できるよね?」
テトラ「それは、ええと、絶対値は……あ、そうか《定義にかえれ》ですね。 $\ABS{x}$ の定義はこうです」
絶対値 $\ABS{x}$ の定義
$$ \ABS{x} = \left\{\begin{array}{llll} x & \REMTEXT{$x \geqq 0$の場合} \\ -x & \REMTEXT{$x < 0$の場合} \\ \end{array}\right. $$
僕「うん」
テトラ「$x < 0$ のときは、 $\ABS{x} = -x$ ですから、 $x$ が大きくなればなるほど $\ABS{x}$ は小さくなります。 でも、 $x \geqq 0$ のときは、 $\ABS{x} = x$ ですから、 $x$ が大きくなればなるほど $\ABS{x}$ も大きくなります。 ……ですよね?」
僕「そうそう、それで説明になっているよ。減っていく(つまり、グラフは下がる)のと、増えていく(つまり、グラフは上がる) というのが $0$ を境目にして切り替わっている」
テトラ「はい、そうです」
僕「だから、 $y = \ABS{x}$ という関数の増減表はこう書ける」
増減表($y = \ABS{x}$)
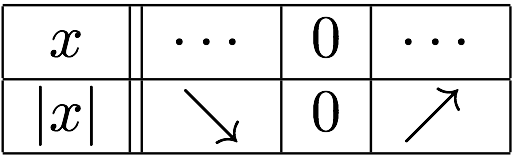
テトラ「ははあ……増減表」
僕「同じように、 $y = x^2$ も考えることができる。 $2$ 乗しているので、 $x$ が $0$ でも正でも負でも $x^2$ は $0$ 以上。 そして、 $0$ を境目にして、 $x < 0$ のときは $x^2$ は減少関数になってて、 $x \geqq 0$ のときは $x^2$ は増加関数になっている。 こちらも増減表を書ける」
増減表($y = \ABS{x}$ と $y = x^2$)
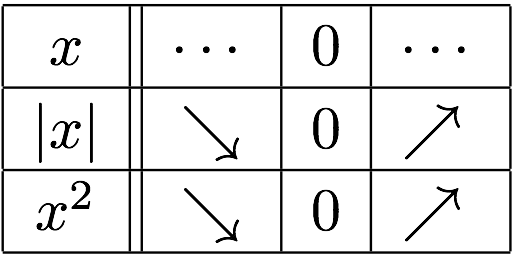
テトラ「はいはい。 $y = \ABS{x}$ と $y = x^2$ の増減表は同じになるということですね!」
僕「そうだね。グラフは関数をとらえるいい道具だけど、増減表もいい道具の一つだよね」
テトラ「はい……グラフと増減表」
テトラちゃんは《秘密ノート》を取り出してさっとメモを取る。
僕「グラフを与えられて方程式を求めるというのは意外に難しいよね」
テトラ「そうですね。方程式からグラフを描くのなら《根気よく試す》という手が使えるんですが……」
僕「具体的な数を代入してみるってこと?」
テトラ「そうです。 $x = 0$ のときはどうか、 $x = 1$ のときはどうか……」
僕「グラフから方程式を求めるのは少し練習が必要かも。たとえばこんな問題はどう?」
問題2
以下のグラフを表す方程式を答えよ。
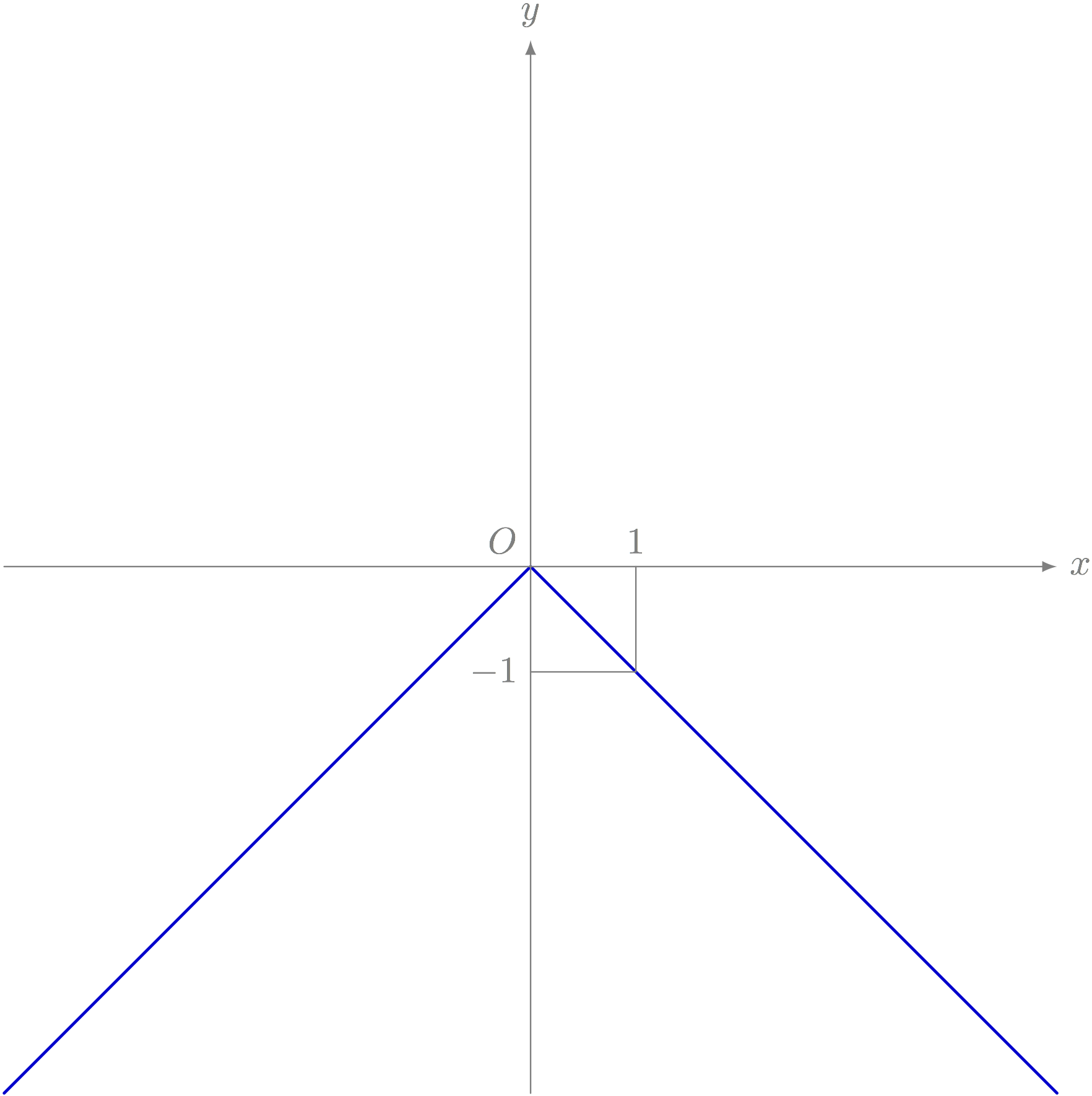
テトラ「あ、これは簡単です」
僕「そう?」
テトラ「え、簡単……ですよね?」
僕「じゃあ答えてみて」
テトラ「はい、 $y = -\ABS{x}$ です」
僕「はい、正解」
解答2
$ y = -\ABS{x} $

テトラ「よかったです」
僕「$y = -\ABS{x}$ のグラフと $y = \ABS{x}$ のグラフとは《$x$ 軸を対称軸として線対称の関係にある》よね」
テトラ「あ、はい、そうですね。 $x$ 軸でぱたりと裏返した関係です」
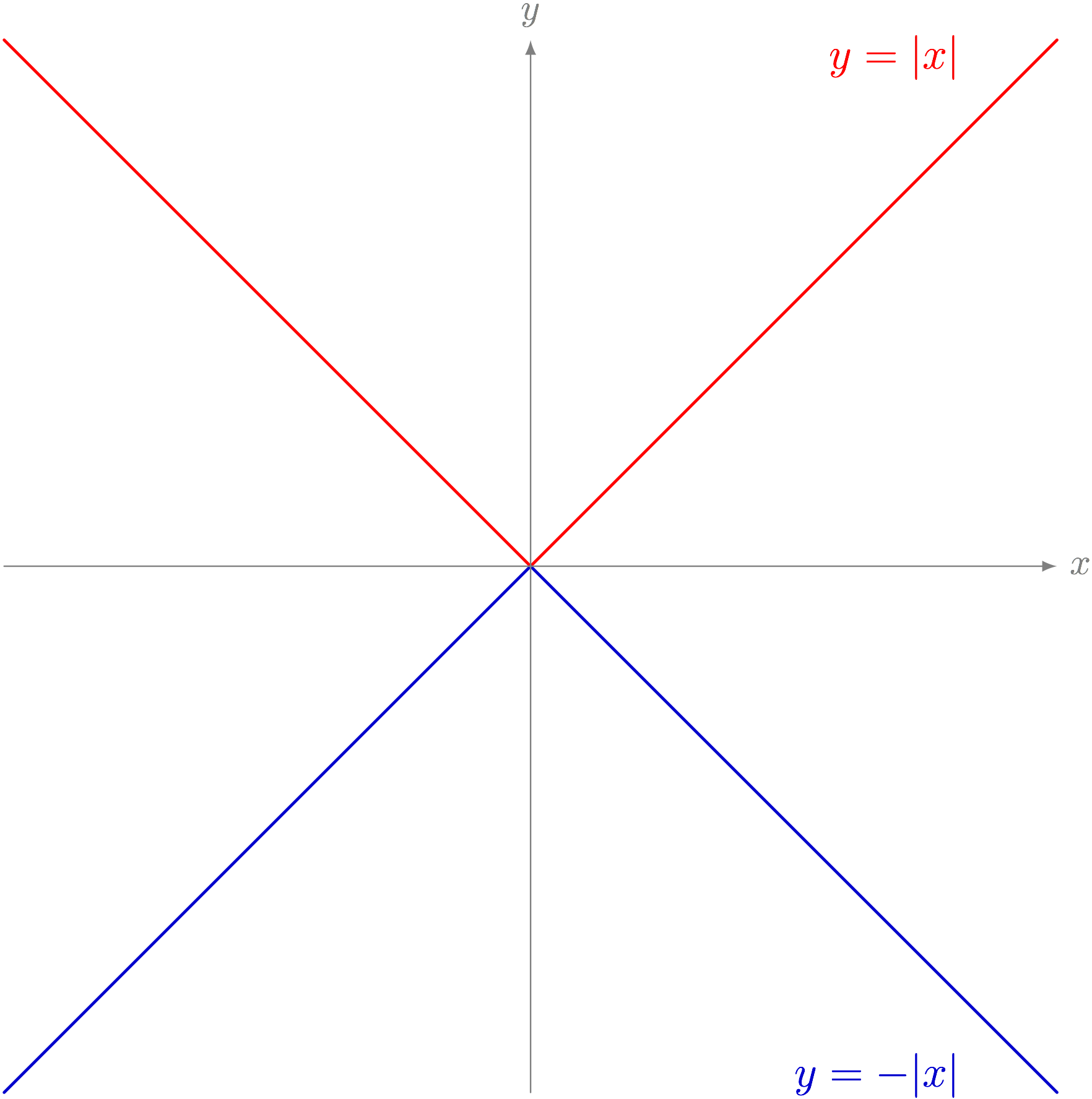
僕「そういうこと。じゃあ、次の問題だよ。このグラフの方程式は?」
問題3
以下のグラフを表す方程式を答えよ。
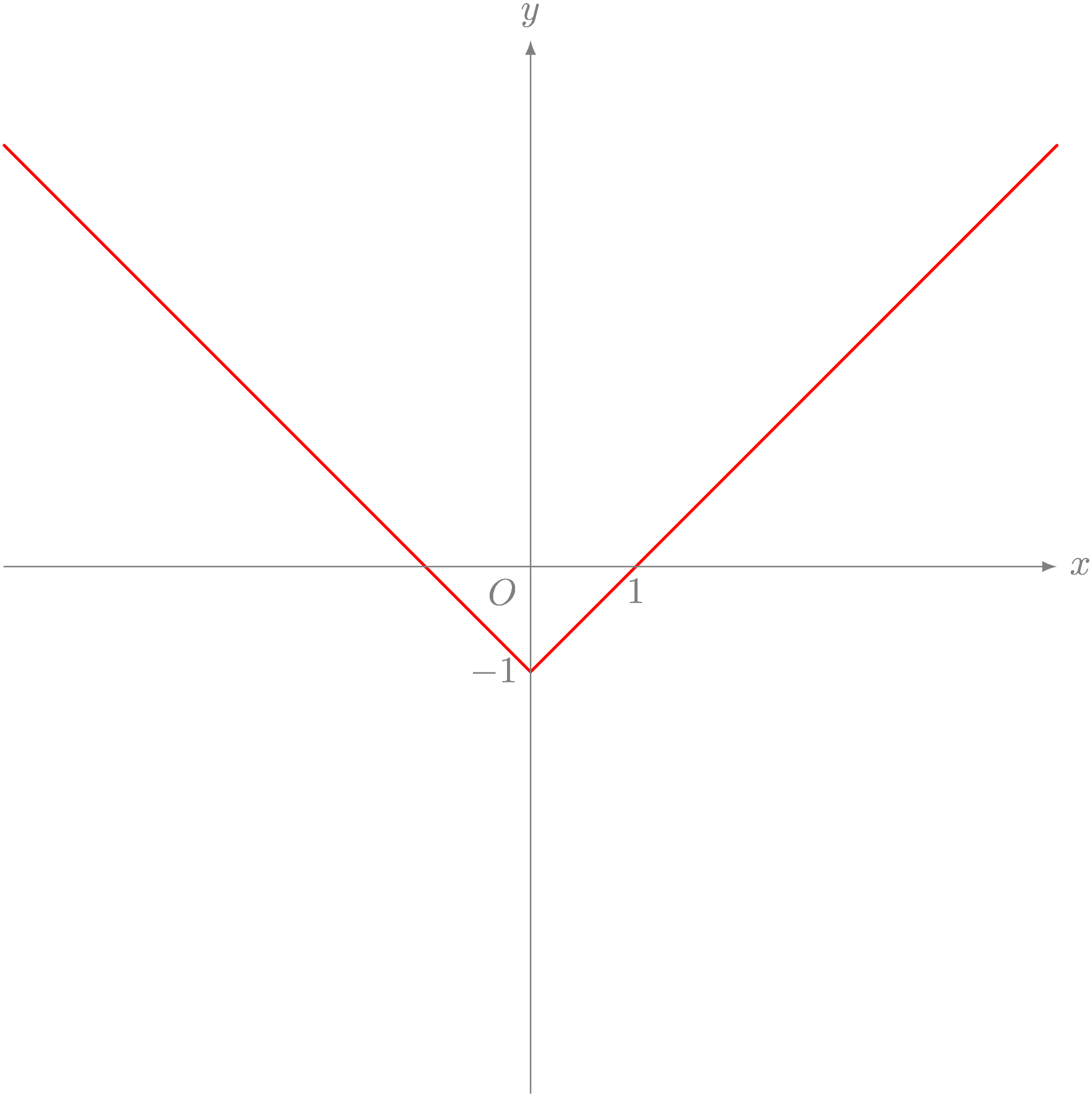
テトラ「先輩……これはもうわかりますよう!」
僕「じゃあ、答えは?」
テトラ「はい、これは $y = \ABS{x} - 1$ です!」
僕「はい、正解」
解答3
$ y = \ABS{x} - 1 $

テトラ「これは、あれですよね。 $y = \ABS{x}$ のグラフを $1$ だけ下げたんですよね?」
僕「そうそう。そこまでわかっているなら、これもすぐ解けるかなあ」
問題4
以下のグラフを表す方程式を答えよ。
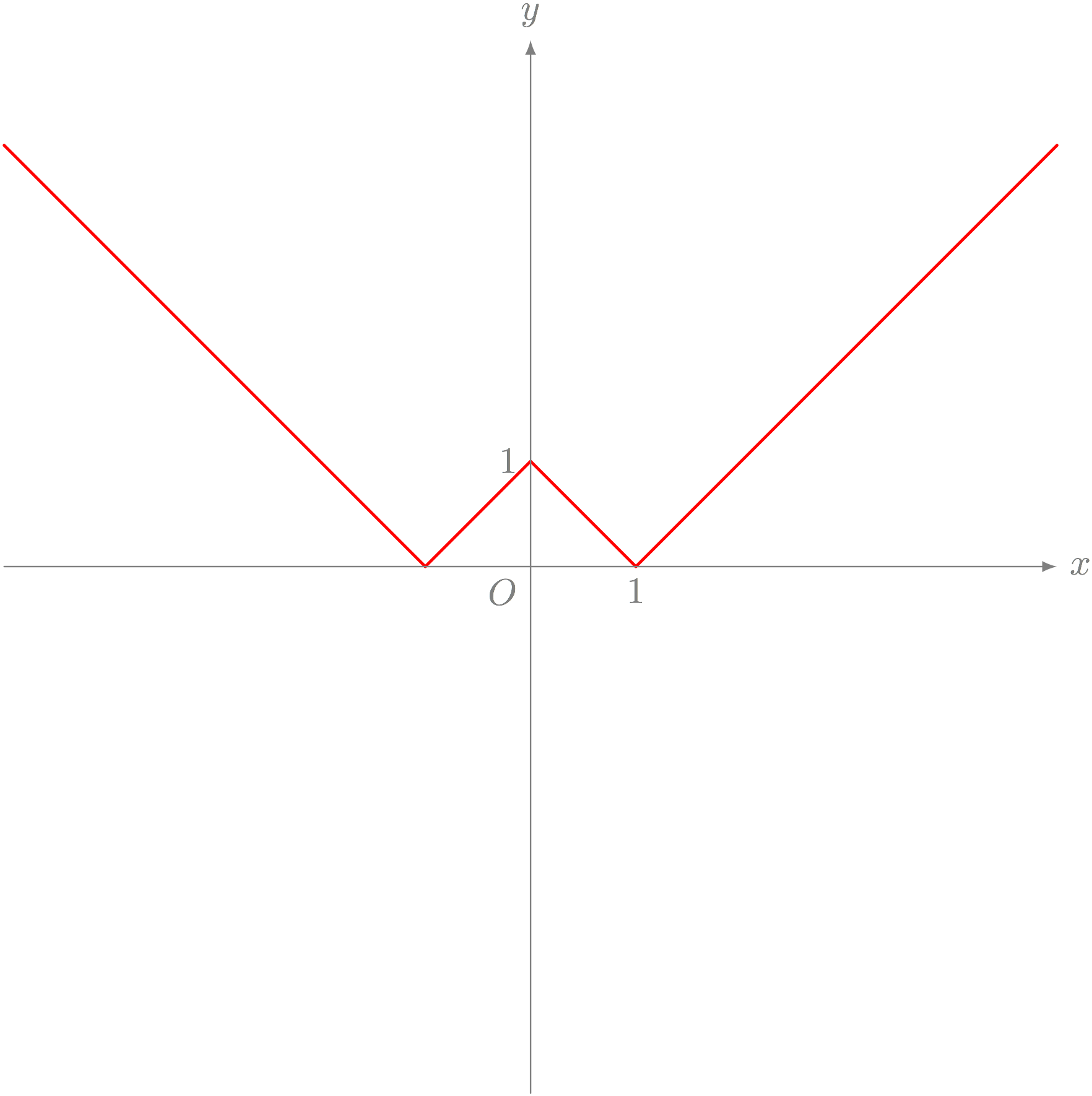
テトラ「え……これは?」
僕「これもすぐに解ける?」
テトラ「ちょっと待ってください……考えます」
テトラちゃんは熟考に入ってしまった。
ノートに図をいくつか描き、しばらくして顔を上げた。
僕「できた?」
テトラ「い、いちおう出来たんですが……」
僕「どんな方程式になったの?」
テトラ「ちょっと恥ずかしいんですが」
テトラちゃんの解答4
$$ y = \left\{\begin{array}{llll} \ABS{x} - 1 & \REMTEXT{$x \leqq -1$の場合} \\ -\ABS{x} + 1 & \REMTEXT{$-1 < x < 1$の場合} \\ \ABS{x} - 1 & \REMTEXT{$x \geqq 1$の場合} \\ \end{array}\right. $$

僕「ああ、なるほどなるほど。そうやったんだね」
テトラ「合ってるでしょうか?」
僕「うん、合ってるよ。テトラちゃんは三つの場合に場合分けしたんだね」
テトラ「はい、そうです。 最初はギザギザにびっくりしたんですが、 でもポリアさんの問いかけ《似ているものを知らないか》を考えると、 これって、先ほど先輩が出した問題の $y = \ABS{x} - 1$ に似てるって思ったんです」
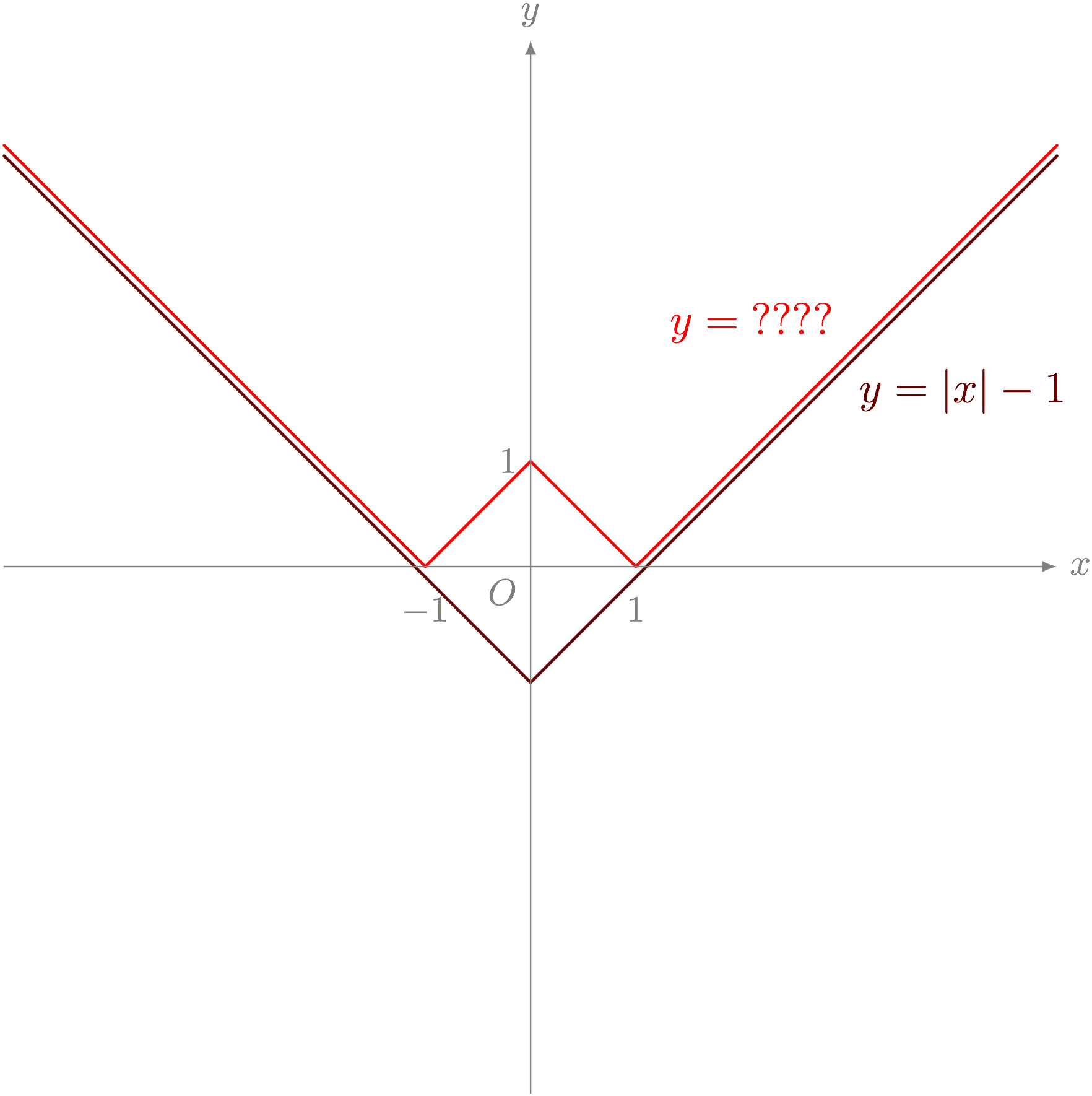
$y = \ABS{x} - 1$ と似てる?
僕「なるほど。ポリアの問いかけ、大活躍だ」
テトラ「あの、それで、二つの違いって、この真ん中の《とんがり部分》だけですよね。 $-1 < x < 1$ の範囲だけが違います。 なので、このとんがり部分をどう作るのかを考えました。 そして、ちょうど、 $y = \ABS{x} - 1$ を $x$ 軸でぱたんと裏返した、 $y = -(\ABS{x} - 1) = -\ABS{x} + 1$ を使えば作れると思ったんです!」
僕「うんうん。だから、 $\ABS{x} - 1$ と $-\ABS{x} + 1$ を使ったんだね。 $x$ の範囲に応じて場合分けして」
テトラ「そうです! ……でも先輩の答えは別なんですよね」
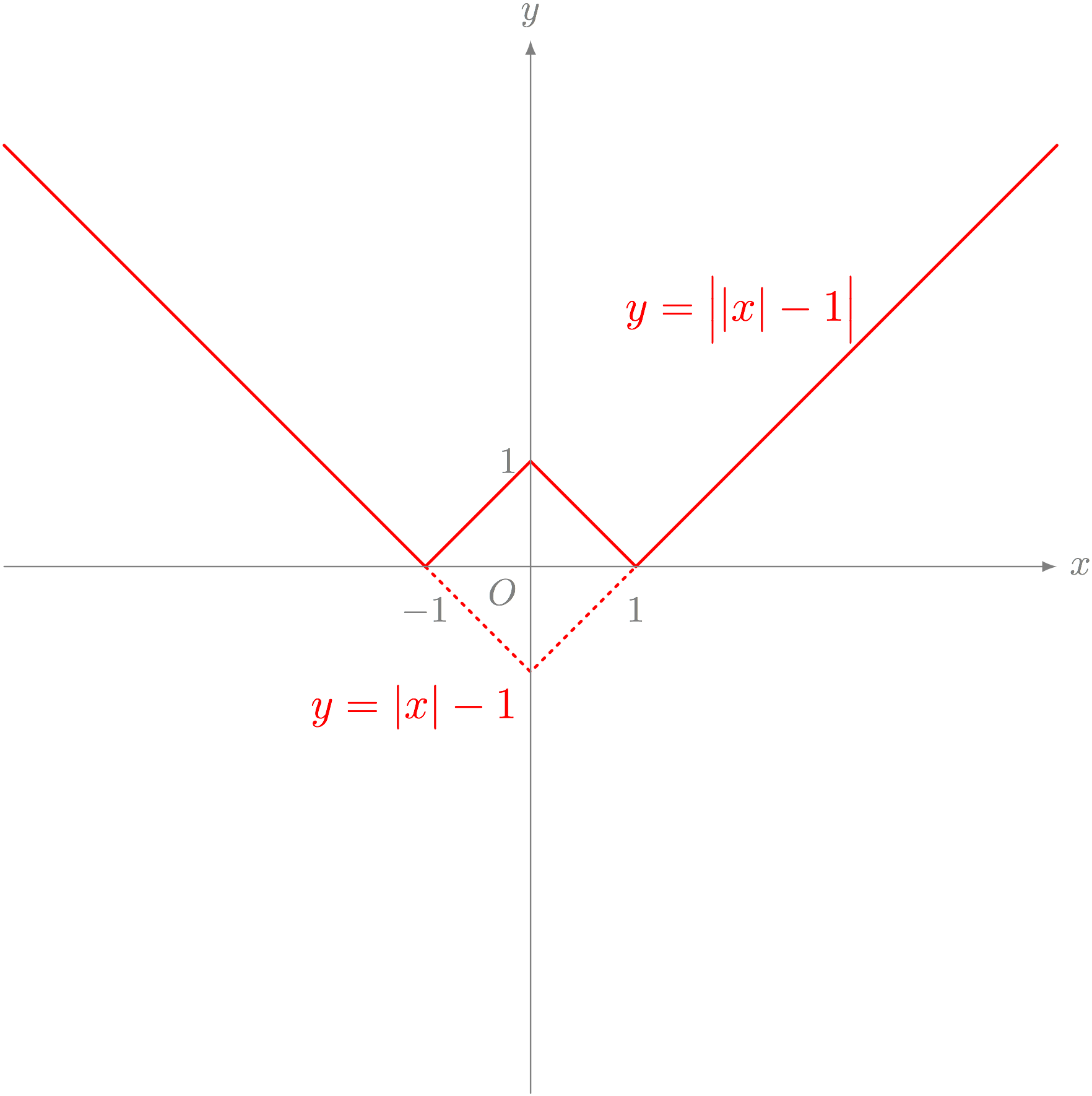
僕「僕が考えた答えはこうだよ。 $y = \BIGABS{\ABS{x} - 1}$」
解答4
$ y = \BIGABS{\ABS{x} - 1} $

テトラ「絶対値を二重に!?」
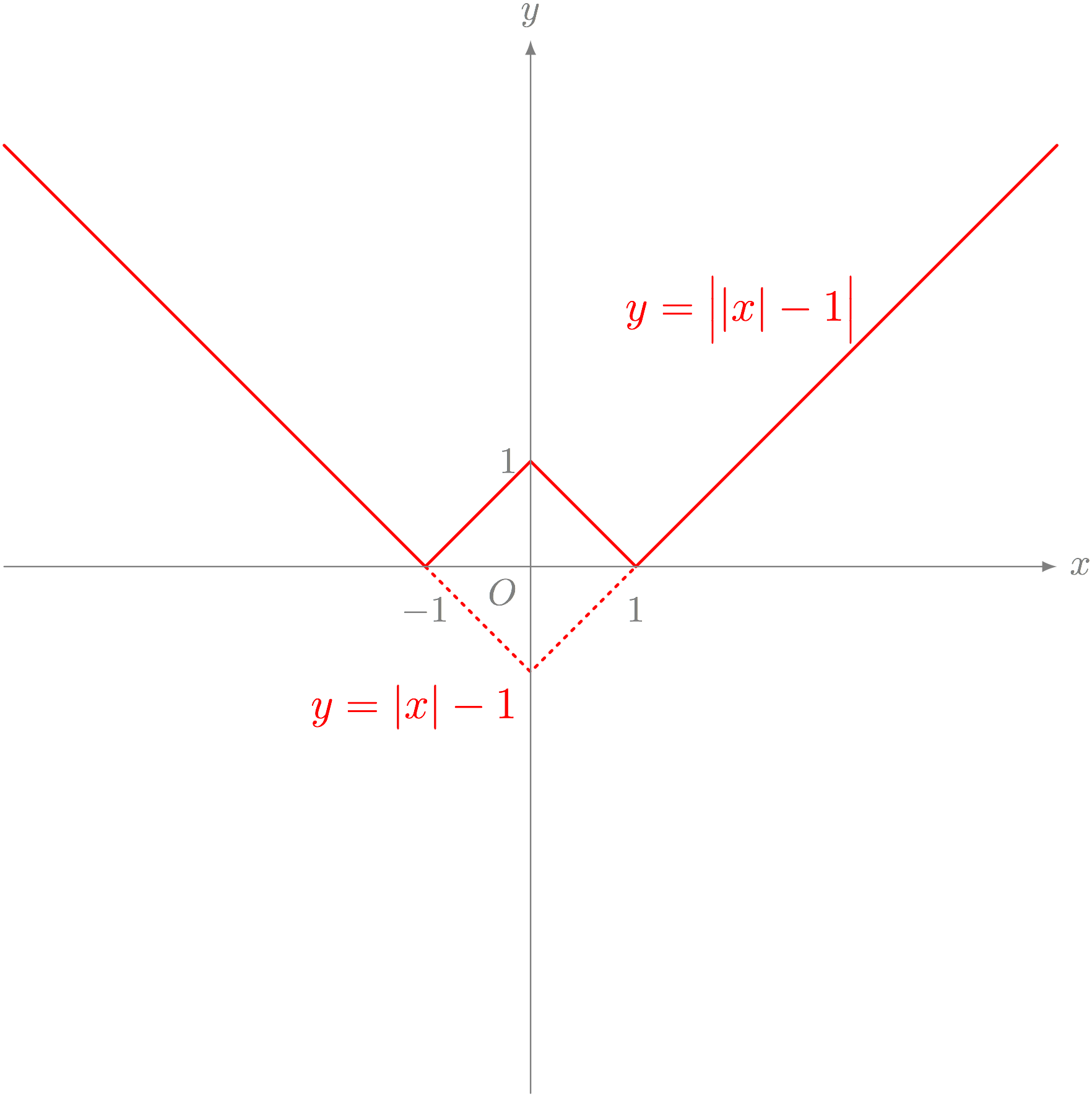
僕「僕も、テトラちゃんが《とんがり部分》と呼んだところをどうするか考えた。 テトラちゃんは $y = -\ABS{x} + 1$ という関数でとんがり部分を作ったけど、 僕は $y = \ABS{x} - 1$ のグラフの $x$ 軸よりも下になる部分だけを上に《折り返せばいい》と思ったんだ。 $x$ 軸よりも下のところだけを上に折り返すというのは、 プラスの部分はそのままで、マイナスの部分をプラスにしてやるってことだから、 絶対値を使えばいいと思ったんだよ」
絶対値で $x$ 軸より下を折り返して、 $y = \ABS{x} - 1$ から $y = \BIGABS{\ABS{x} - 1}$ を作る
テトラ「なるほどです!」
僕「もちろん、テトラちゃんのように場合分けをしてもまちがいというわけじゃないよ。 結果的には同じグラフになるし」
テトラ「折り返すために絶対値を使うっておもしろいです!」
僕「そもそも、 $y = \ABS{x}$ のグラフも折り返していると見なせるけどね」
テトラ「どういう意味ですか?」
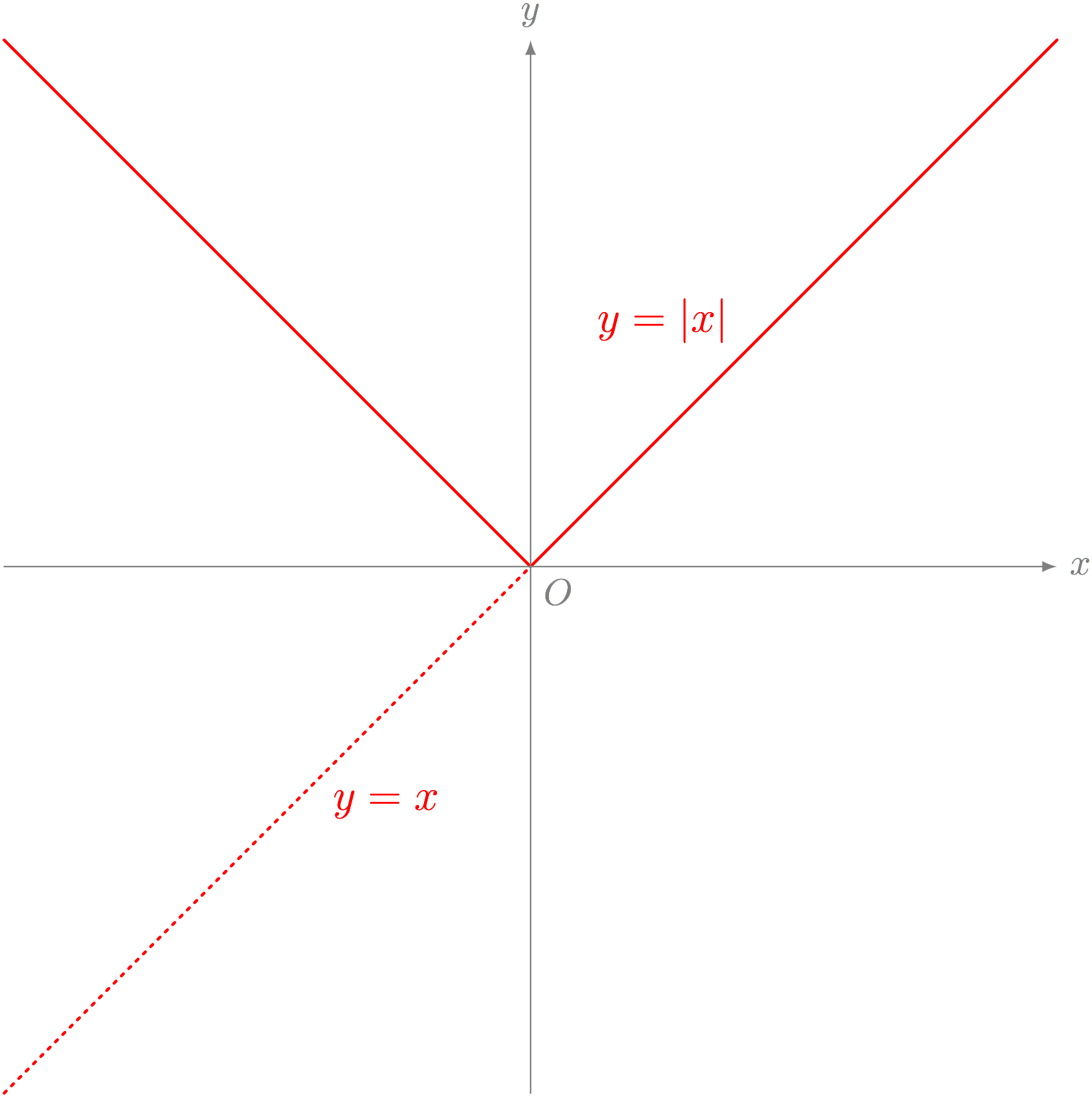
僕「$y = x$ という関数のグラフを考えて、 $x$ 軸よりも下のところを折り返したのが $y = \ABS{x}$ のグラフといえるってこと」
絶対値で $x$ 軸より下を折り返して、 $y = x$ から $y = \ABS{x}$ を作る
テトラ「ははあ……言われてみれば、確かに! グラフっていろんな見方が出来るんですね!」
僕「そうだね。たとえばさっきの問題4で場合分けするときも、別の範囲で分けられるよ。こんなふうに」
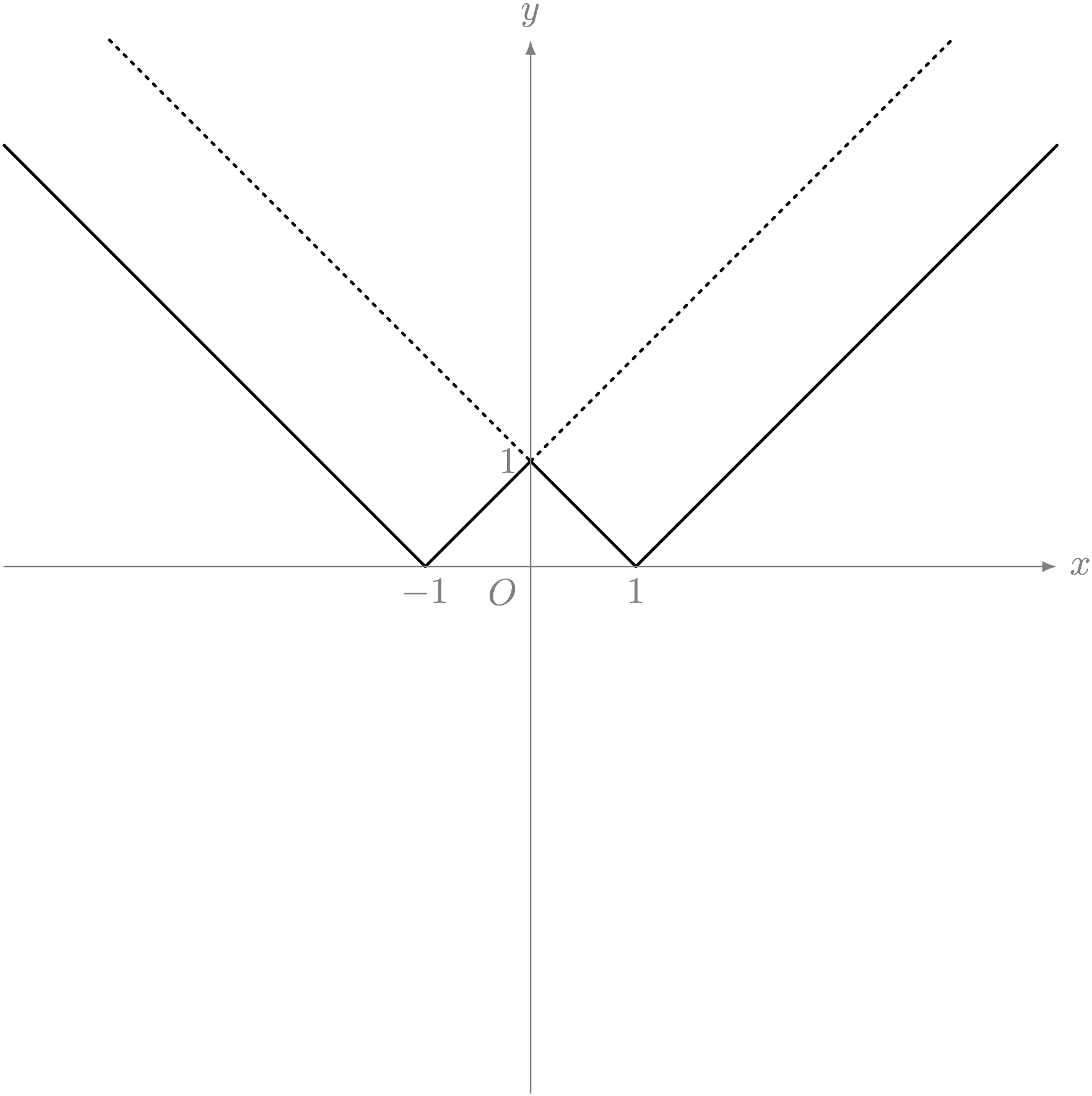
解答4'
$$ y = \left\{\begin{array}{llll} \ABS{x + 1} & \REMTEXT{$x < 0$の場合} \\ \ABS{x - 1} & \REMTEXT{$x \geqq 0$の場合} \\ \end{array}\right. $$
テトラ「え……これは?」
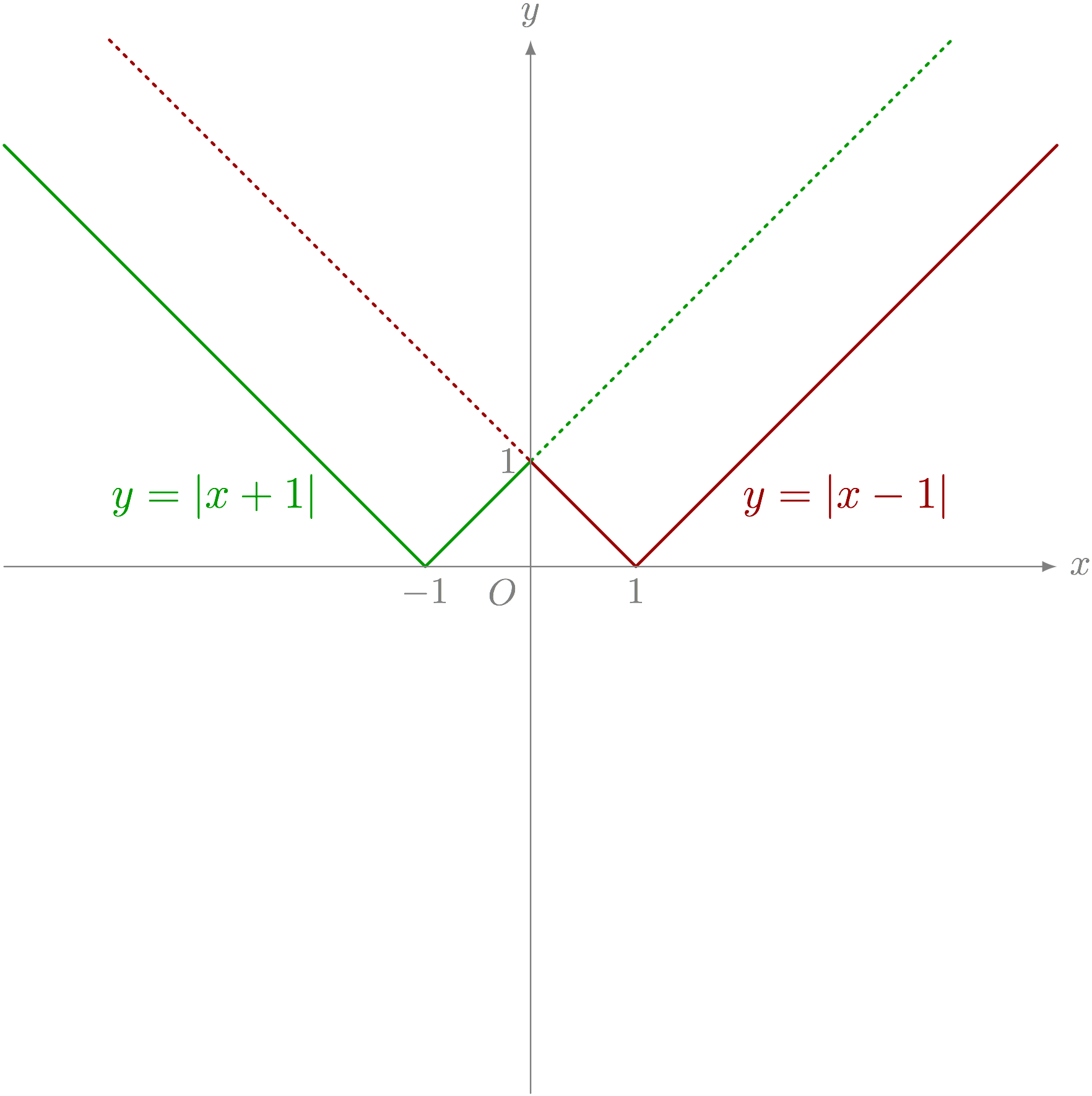
僕「つまり、真ん中にとんがり部分があるという見方をやめたんだね。 $y = \ABS{x}$ というグラフを左に $1$ 動かしたのと、右に $1$ 動かしたのを合わせたグラフだと考えたんだよ。 これで、 $y = \ABS{x+1}$ と $y = \ABS{x - 1}$ から $y = \BIGABS{\ABS{x} - 1}$ を作ったことになる」
$y = \ABS{x+1}$ と $y = \ABS{x - 1}$ から $y = \BIGABS{\ABS{x} - 1}$ を作る
テトラ「なるほどです! おもしろいですねえ……」
僕「おもしろいよね」
テトラ「む、むむむむむっ!」
僕「どうしたの?」
テトラ「先輩! 発見、はっけん! 先ほど先輩は、 $y = \BIGABS{\ABS{x} - 1}$ という方程式をお答えになりましたよね」
僕「うん」
テトラ「ここに出てくる《二重になった絶対値》が、ちょうど《二回の折り返し》に対応しているってことですね!」
僕「そうだね。テトラちゃんの言うとおり。 $\BIGABS{\ABS{x} - 1}$ の式を組み立てていく様子は、 そのまま図形を作っていく様子と対応しているよ」
ステップ1. グラフ $y = x$ を描く
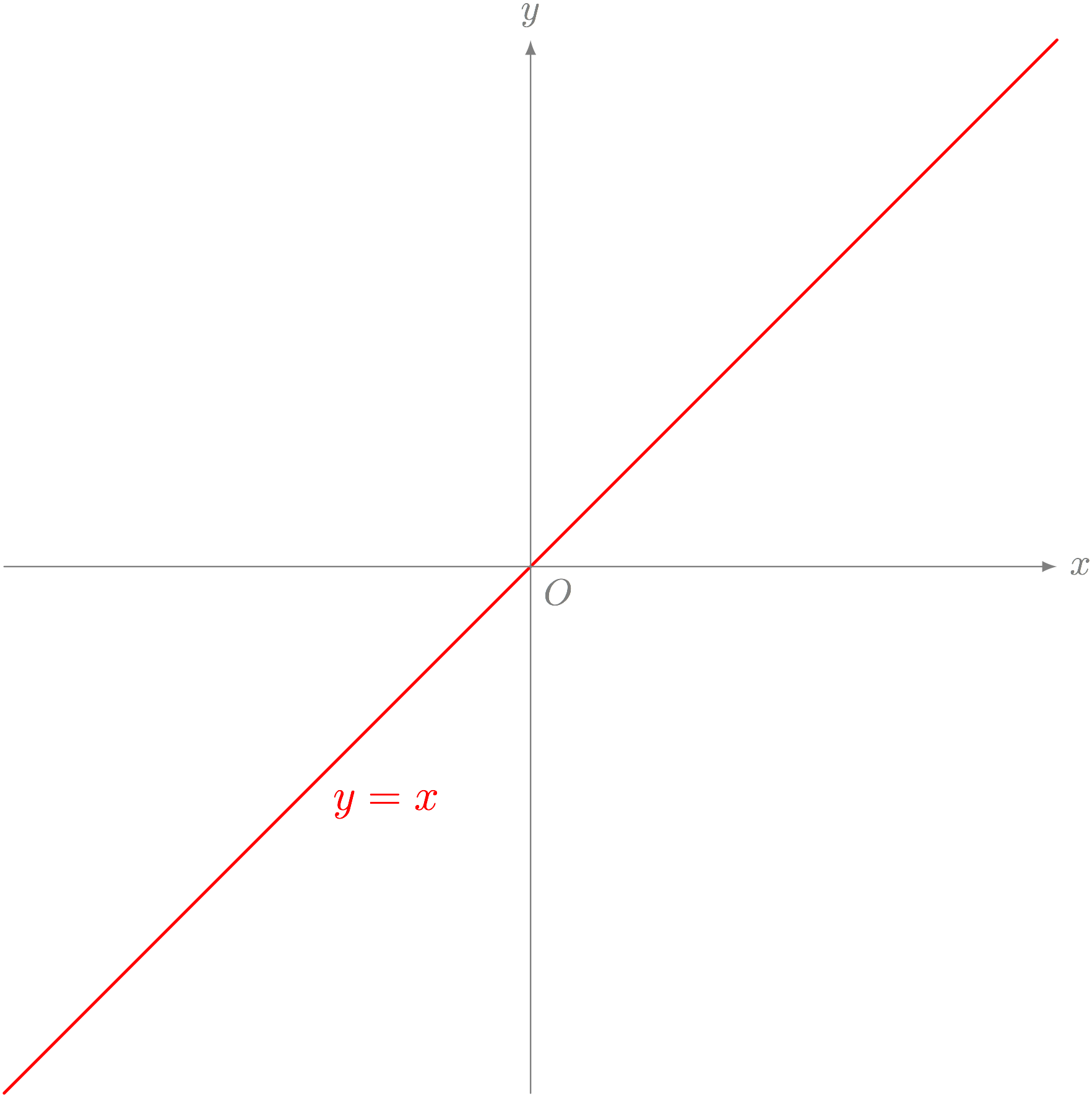
ステップ2. グラフ $y = x$ を《$x$ 軸で折り返す》と、グラフ $y = \ABS{x}$ ができる
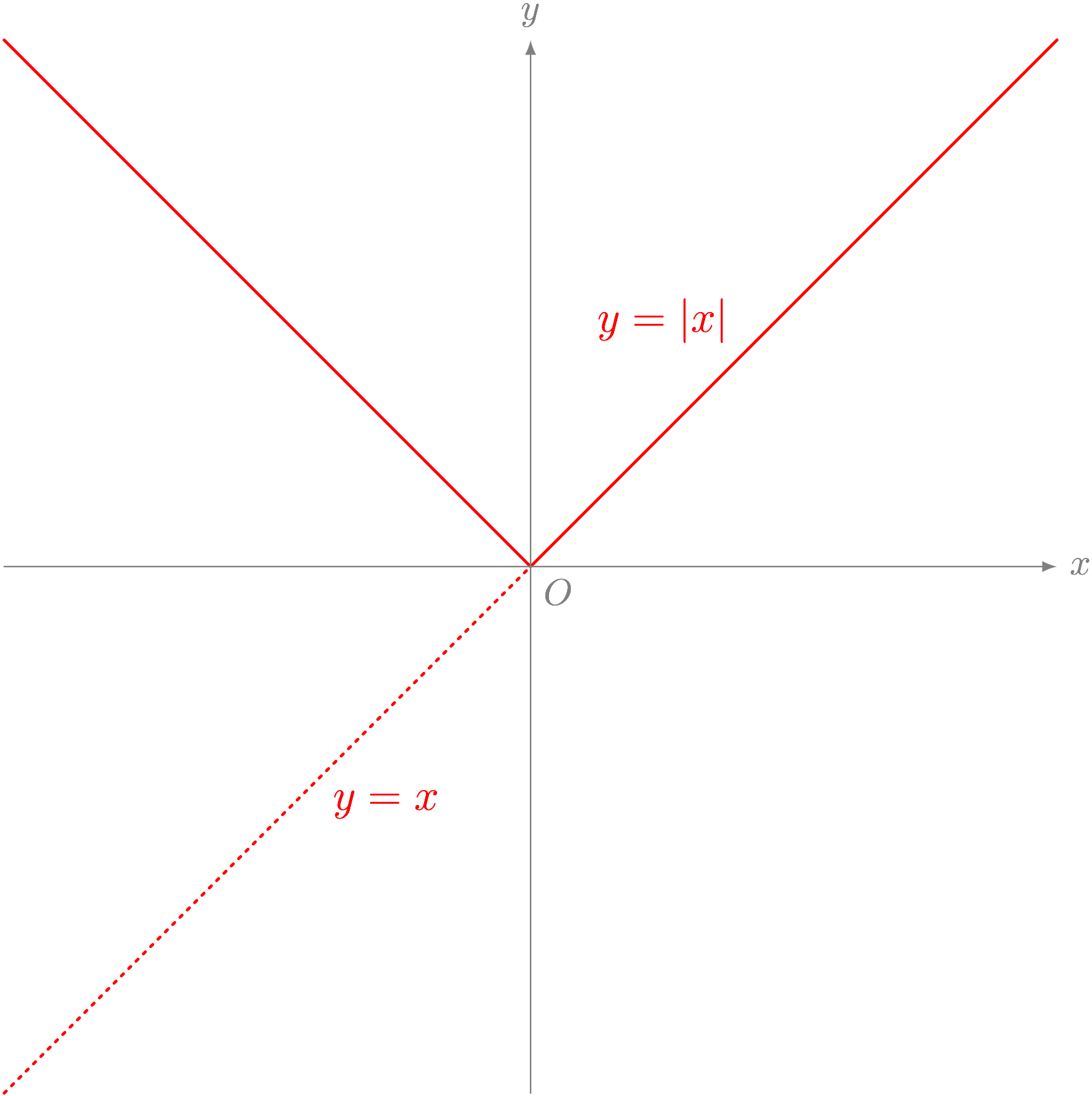
ステップ3. グラフ $y = \ABS{x}$ を《$1$ 下げる》と、 $y = \ABS{x} - 1$ ができる
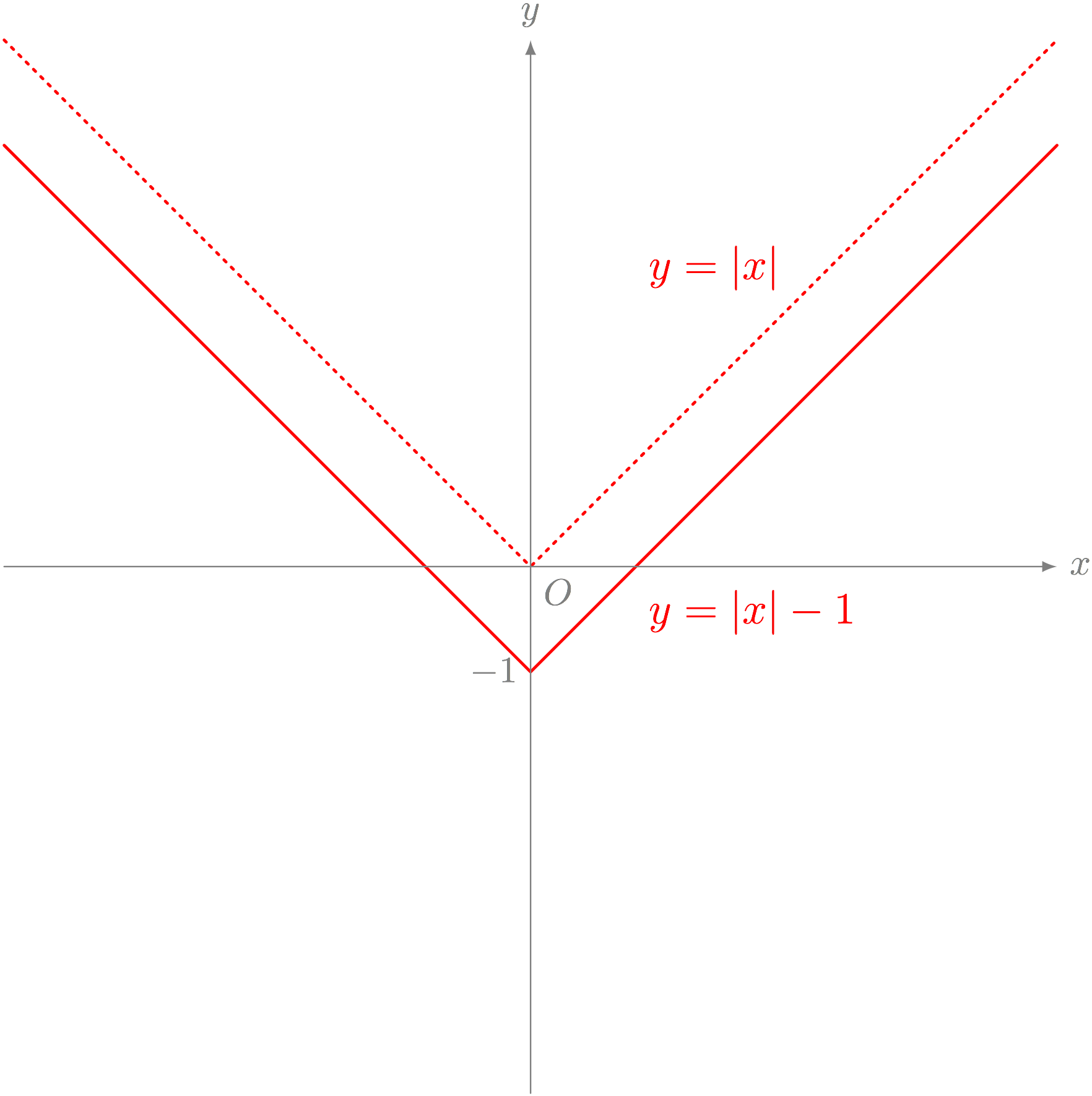
ステップ4. グラフ $y = \ABS{x} - 1$ を《$x$ 軸で折り返す》と、 $y = \BIGABS{\ABS{x} - 1}$ ができる
テトラ「すみません。何だか一人で興奮してしまって……考えてみると、当たり前です」
僕「いやいや、大事なことだよ」
テトラ「数式を組み立てていくのと、グラフを作っていくのがきちんと対応しているのはおもしろいです……」
僕「そうだね」
テトラ「む、むむむむむっ!」
僕「どうしたの?」
テトラ「先輩! あたし、すごい問題おもいついてしまいましたっ!」
僕「問題?」
テトラ「これです!」
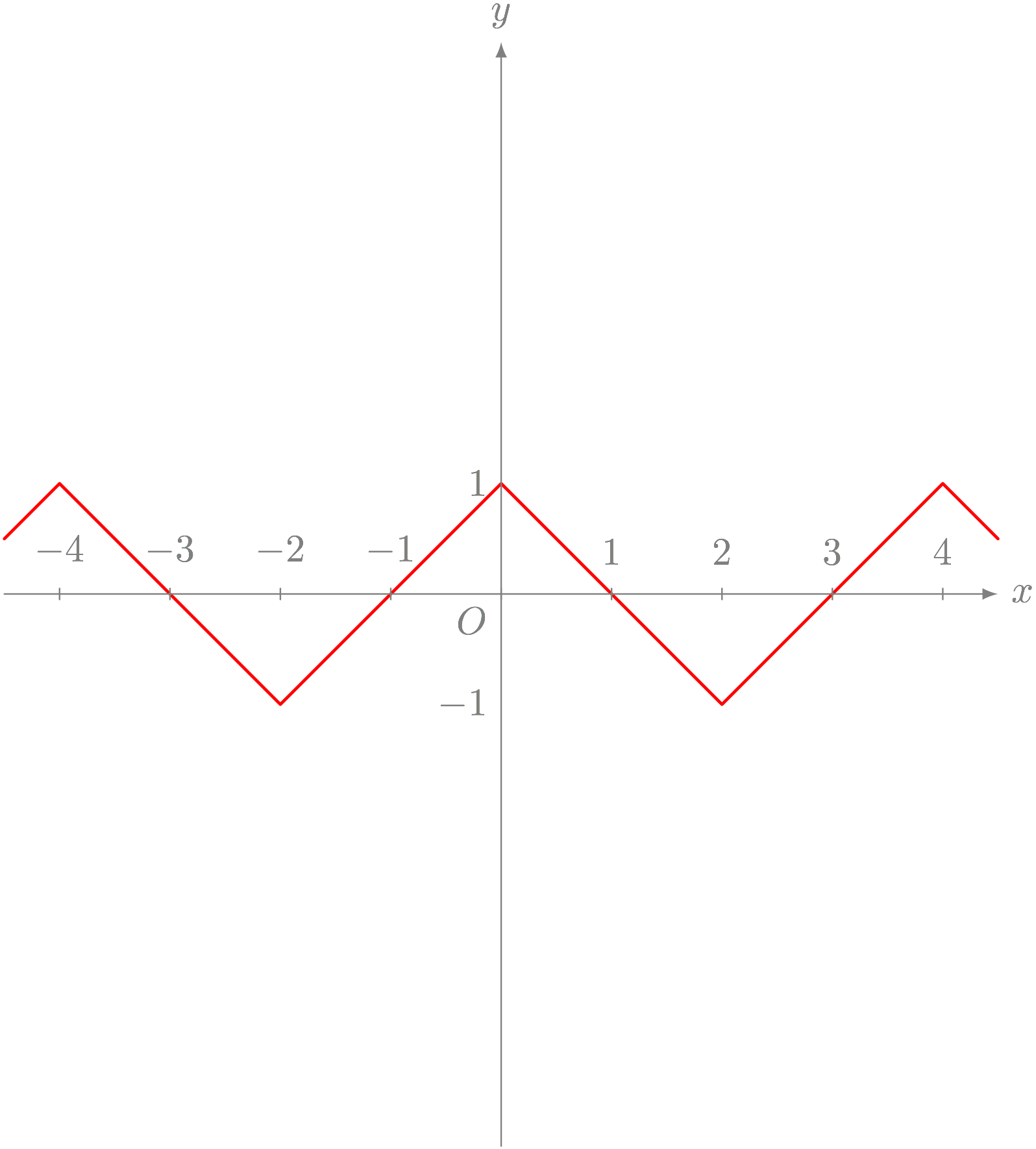
問題X
以下のグラフを表す方程式を答えよ。
僕「おっと!」
テトラ「このジグザグはどんな式で表せるんでしょうか?!」
僕「……このグラフ、ずっと続いているってことだよね?」
テトラ「はい、そうですっ! 無限のかなたから、無限のかなたまで!」
テトラちゃんは、大きな目をキラキラさせて僕を見つめている。
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第81回終わり)
(2014年7月4日)