第55回 シーズン6 エピソード5

おいしい掛け算の作り方（前編）

僕の部屋

ユーリ「いつ教えてくれんの？」

僕「何の話？」

ユーリ「年下だから何なの？」

僕「だから、地の文に突っ込むなよ。 それより、部屋に入ってくるなり『いつ教えるの？』って何のこと？」

ユーリ「掛け算の話！　掛け算もあるっていってたじゃん！　あれから考えてたけど、 矢印の掛け算なんて想像もつかないよ」

僕「ああ、ベクトルの掛け算の話か」

ユーリ「《スパゲティコール》だよ、確か」

僕「だから地の文に……まあいいや。とにかく、ベクトルの掛け算の話を聞きたいんだね」

ユーリ「納得いかないと許さないゾ☆」

僕「いや、それ、キャラ変わってるから」

ベクトルの掛け算

僕「ベクトルの掛け算は二種類あるんだけど、そのうちの一つ内積（ないせき）の話をしよう」

ユーリ「ないせき？」

僕「そう。内部の《内》と掛け算の《積》で内積。どうして内部なのかは知らないけど……」

ユーリ「その、えーと、内積がベクトルの掛け算になるの？」

僕「そうだね。数の掛け算とはちょっと違うけれど、掛け算に似ている新しい演算だね」

ユーリ「えんざんって何？」

僕「まあ計算みたいなものだと思えばいいよ。 足し算も、引き算も、掛け算も、割り算も、みんな演算と呼んでいい。 あ、そうだ。余りを求める計算も演算と呼んでいい」

ユーリ「ふーん。そんで？」

僕「数の掛け算の場合、二つの数を掛けた結果は数になるよね」

ユーリ「？　当たり前じゃん。 $2 \times 3 = 6$ で $2$ も $3$ も $6$ も数だよ」

僕「そうそう、そういうこと。でも、ベクトルの掛け算……ベクトルの内積はちょっと違う。 二つのベクトルの内積を計算した結果は数になるんだ」

ユーリ「おんなじじゃん。結果は数になるんでしょ？」

僕「あ……いや、うん。そういう意味なら同じなんだけど、お兄ちゃんが言いたいのは、 二つのベクトルの内積を計算した結果はベクトルにならないということ」

ユーリ「ふーん……」

僕「あれ？　ノリ悪いな」

ユーリ「それ、大事な話？」

僕「そうだよ。中学校では計算というと数の話だけだよね。 数以外のもの、たとえばベクトルの計算は習わない」

ユーリ「まーそーだけど」

僕「だから、何を計算するか、計算結果が何になるか、ということはあまり気にしない。 だって、ぜんぶ数に決まってるから」

ユーリ「ふんふん」

僕「でも、僕たちはいま数じゃないもの……数以外の数学的対象を扱おうとしている。 だから、何と何を計算して結果が何なのかを意識するのは大事なんだ」

ユーリ「わーった。それで、何だっけ。ベクトル掛けるベクトルが数？」

僕「うん。きちんと《内積》という言葉を使おう。二つのベクトルの内積を計算すると数になる」

ユーリ「どんな数？」

僕「これが、内積の定義だよ。簡単のため、平面上のベクトルで考えることにするね」

ユーリ「なにこれめんどい」

僕「これが、内積の定義だね。数学者がこんなふうに定義したんだ」

ユーリ「ごめん、お兄ちゃん。降参だよ」

僕「今日は何だか弱気だな」

ユーリ「降参だよ……高三で習うまで待つよ」

僕「……そのギャグ、スルーしていいかな」

ユーリ「いろいろわかんない。この縦棒 $|$ は何だっけ、絶対値だっけ？　ベクトルの絶対値って何？」

僕「うん、そうだよね。一つ一つの表記を理解しなかったら《これが内積の定義です》っていわれても困る」

ユーリ「そーそー。ちゃんと教えるのじゃ」

僕「いきなり年取るなよ。まず、 $|\vec a|$ という書き方は確かに絶対値のようなものなんだけど、 これはベクトルの大きさを表している。矢印を想像するなら、その矢印の長さだね。 これは必ず $0$ より大きな数になる。向きは関係がない」

ユーリ「え？　矢印の長さなら、 $0$ 以上じゃないの？」

僕「あ、そうそう。ごめんごめん。ベクトルの大きさは $0$ のこともあるからね。 $0$ より大きな数じゃなく、 $0$ 以上だ」

ユーリ「しっかりしてよね」

僕「それから、内積の定義を読むためには《ベクトルのなす角》を理解しなくちゃいけないね。 でもこれは簡単だよ。こういうこと」

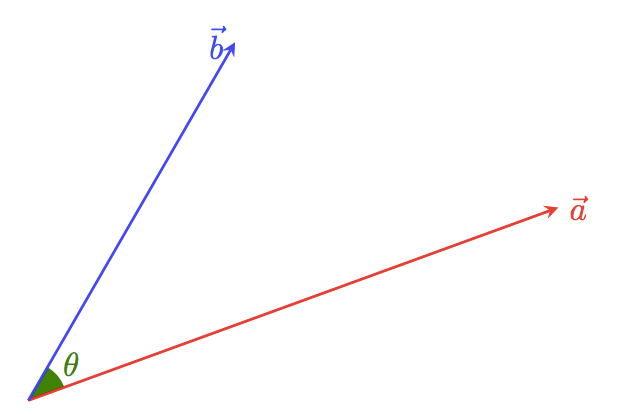
僕「《ベクトルのなす角》っていうのは、《ベクトルが作る角》と同じ意味だよ。 この角 $\theta$（シータ）は、どんな大きさでも取っていいけど、普通は $0$ 度から $180$ 度で考えるかな」

ユーリ「$0$ 度？」

僕「うん、二つのベクトルの向きが一致しているときは角度が $0$ 度。 方向は一致しているけれど向きが正反対のときは角度が $180$ 度ということになる」

ベクトル $\vec a$ と $\vec b$ のなす角が $0$ 度

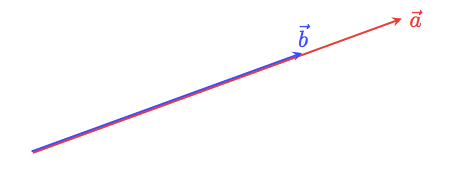
ベクトル $\vec a$ と $\vec b$ のなす角が $180$ 度

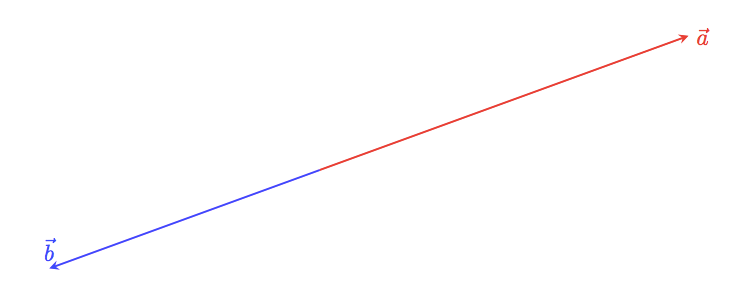
ユーリ「そかそか」

僕「ここまでは大丈夫？　ベクトルの大きさ $|\vec a|$ と、二つのベクトルがなす角」

ユーリ「うん！　わかったよ。でもって、問題はこの $\cos$ なんだけど……これは何だっけ、コサインだっけ」

僕「そうだね。内積の定義を理解するには、 $\cos \theta$（コサイン・シータ）が何を表しているかを理解する必要がある」

コサイン

ユーリ「あー、でも前に教えてもらったことあるよね。サインとコサイン」

僕「うん、前に教えたことあるよね。サインとコサイン」

ユーリ「何だっけ、円を描いて……ここがサインとかコサインとか」

僕「そうそう。半径が $1$ の円を描いて、円周の上にある点 $P$ を考えるんだよ。 この説明をするとき、円の中心 $O$ と点 $P$ を結んだ線分のことを動径（どうけい）と呼ぶこともあるね。 動く半径という意味だと思うけど。 で、その点 $P$ の $y$ 座標がサインで、 $x$ 座標がコサインになる。いまはコサインだけを考えようね」

ユーリ「これも《てーぎ》なんだよね」

僕「そうだね。定義だから、まずは《そういうものだ》とそのまま理解しなくちゃいけない。 でも、自分が《ほんとうにわかっているか？》と確かめる必要があるけどね」

ユーリ「どゆこと？」

僕「あのね、定義だからといって何も考えず丸暗記してもしょうがないということ。 丸暗記してもいいんだけど、その定義が何を表しているのかは、ちゃんとわかってほしいんだよ」

ユーリ「意味わかんない」

僕「え？　だからね、 $\cos \theta$ の定義といっても、 《ハンケイ $1$ のエンのエンシュウのウエに……》という言葉だけを呪文のように覚えても、 何を表しているかわかってなければ意味ないっていうこと」

ユーリ「そんなのあたりまえじゃん！」

僕「そう？　じゃあ、ユーリは $\cos \theta$ の定義を理解しているといえる？」

ユーリ「もちろんだよー」

僕「じゃ、お兄ちゃんに説明してみせてよ」

僕は机に広げていた紙を裏返して、新しい紙を広げる。

ユーリ「あっ！　隠さないでよー」

僕「いやいや、ほらここに白い紙がある。ここに図を描いて説明してごらんよ。 $\cos \theta$ の説明」

ユーリ「うー。説明、めんどいんだよー……っと、こうかにゃ」

ユーリの説明図

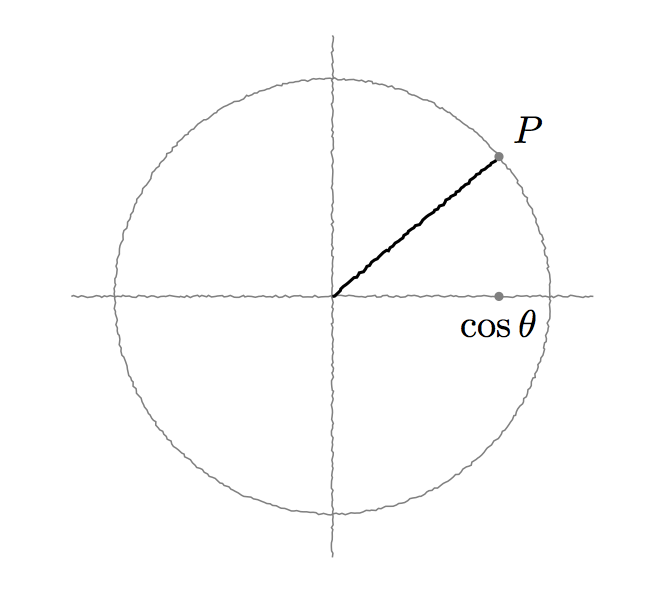
僕「それで？」

ユーリ「うん。だからね。この点 $P$ の下の点がコサイン・シータ！……でしょ？」

僕「まあ、そうだね」

ユーリ「やた！　ねー、わかってるでしょー？」

僕「うん、ユーリの説明している様子を見ていると、ちゃんとわかっているってわかるよ。 でも、細かいところもちゃんと描いたほうがいい」

ユーリ「細かいところって？」

僕「ほら、お兄ちゃんが描いた図と比べてごらんよ。 お兄ちゃんは $x$ 軸と $y$ 軸に名前を付けてるし、 点から $x$ 軸のほうに点線を描いてるだろ？ それに半径が $1$ であることと、角度が $\theta$ であることをちゃんと書いてる」

ユーリ「だって……」

僕「こんな風に点線を書いておくと、 $\cos \theta$ は、真上から光を当てたときに $x$ 軸に落ちる《点の影》の場所だってこともはっきりする」

ユーリ「だって、そんなのわかりきってるから……」

僕「うん、そうだよね。お兄ちゃんはユーリがわかりきってるから書かなかったとわかってるよ。 でも、せっかく紙があるんだから、ちゃんと図を描き、ちゃんと必要な文字を書こうよ。 ほら、ユーリはバシッとキメるのが好きだろ。こういうところをちゃんと」

ユーリ「わーったよ！　次はちゃんと書くから！　とにかくユーリは $\cos \theta$ はわかってるの！」

僕「じゃあ、クイズ。 $\theta$ が $0$ 度に等しいとき、 $\cos \theta$ の値は？」

ユーリ「$0$ ……じゃなくて、 $1$ だ」

僕「そうだね。どうして？」

ユーリ「だって、角度が $0$ 度ってことは、点がここ……軸の上だもん」

僕「そうそう。点が $x$ 軸上にある。その $x$ 座標だから $\cos 0^\circ = 1$ になる」

ユーリ「ふふん。何でもきーてよ」

僕「じゃあ、 $\cos 90^\circ$ は？」