第2回 シーズン1 エピソード2

文字と恒等式（後編）

ミルカ「ふうん……《和と差の積は $2$ 乗の差》は、《長方形を正方形に変換する》ということだな」

テトラ「どういうことでしょうか？」

ミルカ「こういうことだよ、テトラ」

ミルカさんはさらさらと図を描いた。

ミルカ「これが $(a + b)(a - b)$ を表す長方形」

僕「あ、なるほど！」

テトラ「これは……？」

僕「ミルカさん！ これは、縦の長さが $a + b$ で、横の長さが $a - b$ になっている長方形だね。 この面積は確かに $(a + b)(a - b)$ になるなあ……かけ算だ」

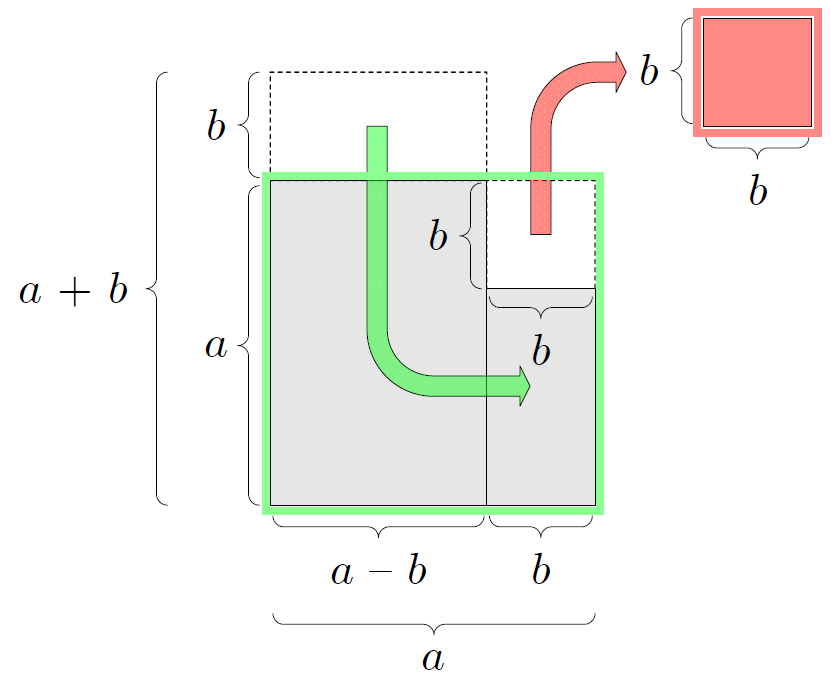
ミルカ「そう。そしてこれが $a^2 - b^2$ を表す図形。二つの正方形で作る」

テトラ「二つの正方形？　どういうことですか」

僕「なるほど！　面積が $a^2$ となっている大きな正方形がまずあって、 その右上の隅から、面積が $b^2$ の小さな正方形を切り取ったんだね」

ミルカ「そう」

ミルカさんは簡潔にそういうと、人差し指をくるくる回す。 彼女は数学を話すとき、ほんとうに楽しそうだ。

テトラちゃんは二つの図をじっと見比べる。 彼女はいつもバタバタしているけれど、数学に向かうときはとても真剣になる。

テトラ「わかりました！　長方形の上にある小さな長方形を、緑色の矢印に従って右下に移動したことになるのですね…… だから、二つの図形の面積は変わらないということですか！」

僕「そうだね！ $(a + b)(a - b)=a^2 - b^2$ と見比べてみると、 左辺の $(a + b)(a - b)$ は長方形の面積を表す。 右辺の $a^2 - b^2$ は大きな正方形の面積から小さな正方形の面積を引いたものになる。 だから、この二つの図形で $(a + b)(a - b)=a^2 - b^2$ が恒等式であることを説明しているんだね」

ミルカさんはゆっくりと頷く。 かすかにシトラスの香りがする。

ミルカ「ここでは図形で説明している。 だから《文字 $a$ と文字 $b$ は $0$ 以上の実数である》という暗黙の仮定が入る。 それさえ忘れなければ、図形的な解釈はなかなか楽しい」

テトラ「え、いまおっしゃったのはどういうことですか？」