![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ユーリ「高校生ってすごいなー!」
僕「ユーリだってすぐにできるよ」
ユーリ「じゃ、何か問題出してみてよ」
僕「じゃあ、たとえばこれは?」
クイズ
次の式を $x$ に関する一次式の積に因数分解せよ。
$$ x^4 - 4x^3 - x^2 + 16x - 12 $$
ユーリ「ほほー……やってみる!」
僕「暗算じゃなくてもいいよ」
ユーリ「えーと……あっ、これ難しーじゃん!」
僕「どうしたいきなり」
ユーリ「だって、最後が $12$ だから、ぜんぶを $x$ でくくれないもん」
僕「そうだね。だからこの $x^4 - 4x^3 - x^2 + 16x - 12$ は $x$ を因子に持たないことになる」
ユーリ「ちぇっ……あ、でもこの問題も $x^4$ だから、こんな感じになりそう」
$$ x^4 - 4x^3 - x^2 + 16x - 12 = (x-a)(x-b)(x-c)(x-d) $$
僕「そうだね。 $x^4$ の係数が $1$ だから、 $x$ の係数が $1$ になっている一次式が $4$ 個になりそうだ。 そんなふうにアタリをつけられる」
$$ \REDFOCUS{x^4} - 4x^3 - x^2 + 16x - 12 = (\REDFOCUS{x}-a)(\REDFOCUS{x}-b)(\REDFOCUS{x}-c)(\REDFOCUS{x}-d) $$
ユーリ「そんじゃ、お兄ちゃんがさっき使ってた謎の方法使うか(第421回参照)」
僕「因数定理だね」
ユーリ「いんすーてーり。 試しに数を $x$ に代入してみるんでしょ。それで $0$ になったらラッキー!」
僕「まあ、そうだね」
ユーリ「たとえば $x$ に $1$ を代入してみる!」
僕「できたね」
ユーリ「やったやった。 $x$ に $1$ を代入したら $0$ になった。てことは……こーかな?」
$$ x^4 - 4x^3 - x^2 + 16x - 12 = \REDFOCUS{(x-1)}(x-b)(x-c)(x-d) $$
僕「そうだね。 $x$ に $1$ を代入したら左辺は $0$ になった。 ということは右辺も $0$ にならなくちゃまずい。 だから $x-1$ を因子に持つことになる」
ユーリ「じゃ、次は $x$ に $2$ を代入する!」
僕「うんうん」
ユーリ「楽勝じゃん。 $x - 2$ が出てきた」
$$ x^4 - 4x^3 - x^2 + 16x - 12 = (x-1)\REDFOCUS{(x-2)}(x-c)(x-d) $$
僕「次は?」
ユーリ「次は $x$ に $3$ を代入してみる……?」
僕「どうしていま、僕の顔を見たんだろう」
ユーリ「ここまでうまく行ったから、何か落とし穴がありそーだと思ったから」
僕「だとしても、顔を見てもしょうがないよね」
ユーリ「ちぇっ、ポーカーフェイス」
僕「……」
ユーリ「おかしい! ここでも $0$ になった!」
僕「別に何もおかしくないよ。素直に行こうよ」
ユーリ「むー」
$$ x^4 - 4x^3 - x^2 + 16x - 12 = (x-1)(x-2)\REDFOCUS{(x-3)}(x-d) $$
僕「じゃ、次は?」
ユーリ「素直に $4$ を代入してみる!」
僕「……」
ユーリ「あっ、けっこうめんどい。 $4^4$ と $4\times 4^3$ は同じだから、ちょうど消えるよね。 それから $4^2$ は $16$ だから、 $16\times 4$ じゃなくて $16\times3$ を計算して……ダメだー。 $0$ になんない!」
$$ \begin{align*} & x^4 - 4x^3 - x^2 + 16x - 12 \\ &= 4^4 - 4\times 4^3 - 4^2 + 16\times 4 - 12 && \REMTEXT{$x$に$4$を代入した} \\ &= \underbrace{4^4 - 4\times 4^3}_{=0} - 16 + 16 \times 4 - 12 \\ &= 16\times 3 - 12 \\ &\NEQ 0 \end{align*} $$僕「ということは、 $x - 4$ は因子にならない。さあさあ、ユーリはどうする?」
ユーリ「お手上げ!」
僕「いやいや、少なくともここまではわかったよね。あともう一歩だ。 $d$ さえわかればいいんだから」
$d$ は何だろうか?
$$ x^4 - 4x^3 - x^2 + 16x - 12 = (x-1)(x-2)(x-3)(x-d) $$
ユーリ「そーだけど……む? むむむむ?」
僕「……」
ユーリ「わかった! $d$ は $-2$ だ!」
僕「おっと、いきなり出たね」
ユーリ「だって、そーじゃん。 $-1$ と $-2$ と $-3$ と $-d$ を掛けたら $-12$ になるはずでしょ? あー、 $x$ に $4$ を代入するのはムダだった!」
僕「こういうことだね。 $$ x^4 - 4x^3 - x^2 + 16x \REDFOCUS{{}-12} = (x\REDFOCUS{{}-1})(x\REDFOCUS{{}-2})(x\REDFOCUS{{}-3})(x\REDFOCUS{{}-d}) $$ だから、 $$ (-12) = (-1)\times(-2)\times(-3)\times(-d) $$ になるので、 $$ d = -2 $$ となる」
ユーリ「できたー」
クイズの答え
$$ x^4 - 4x^3 - x^2 + 16x - 12 = (x-1)(x-2)(x-3)(x+2) $$
僕「お、符号まちがえなかったね。えらいえらい」
ユーリ「ふふん……それにしても、こーゆー引っかけが待ってるとは思わなかったぜ」
僕「え? どこにも引っかけ要素はないよね」
ユーリ「だって、 $1,2,3$ と来たら次は $4$ 試したくなるじゃん。そこが引っかけ」
僕「そうやって、出題者の裏読みばっかりしないほうがいいと思うよ」
ユーリ「ちぇっ」
僕「いまユーリは因数定理を繰り返し使って因数分解したけど、 たとえば $x - 1$ という因子が見つかったところで、多項式の割り算をすることもできるよ」
ユーリ「多項式の割り算?」
僕「こんなふうに筆算して、 数の割り算と同じように $x^4 - 4x^3 - x^2 + 16x - 12$ を $x-1$ で割ることができる」
筆算で $x^4 - 4x^3 - x^2 + 16x - 12$ を $x-1$ で割る
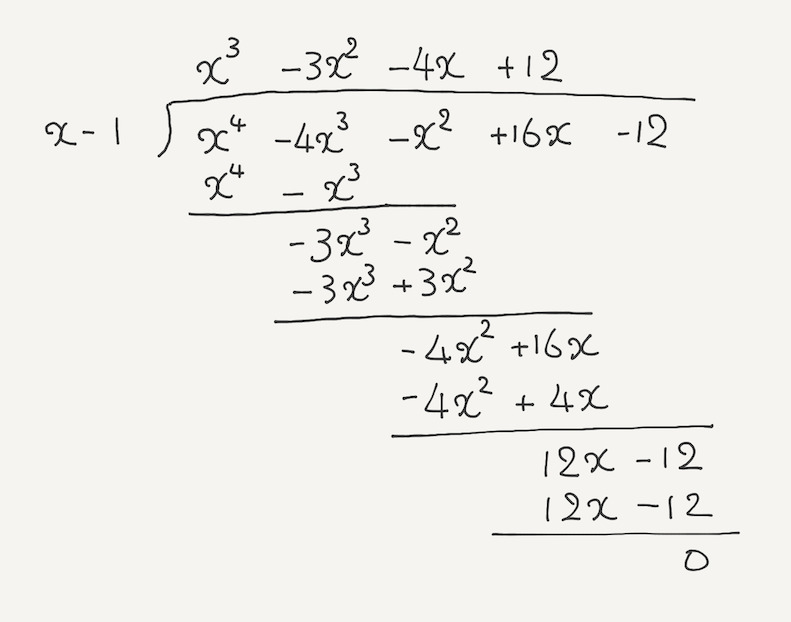
ユーリ「へー……」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2024年5月17日)