![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕とユーリは極座標についておしゃべりをしていた。
極座標で $r = 1$ が単位円を表すという話題を話していたところ(第361回参照)。
ユーリ「ねえお兄ちゃん! 極座標で他の図形も描いてみたい!」
僕「なるほど。じゃあね、こんな問題はどう? これは以前、ミルカさんがテトラちゃんに出した問題だよ」
問題(極方程式)
次の極方程式が表すのはどんな図形か。
$$ r = \theta $$
※偏角 $\theta$ は「度」で表しているとします。
ユーリ「お、おおお?」
僕「さっきは $r = 1$ で単位円を表したよね(第361回参照)。とてもシンプルな式だけど円を表せた。 今度はその次ぐらいにシンプルな式だよね。 $r = \theta$ はどんな図形になるかというと……」
ユーリ「いやいや、お兄ちゃんちょっと待った! そんなにとっとこ話を進めないでよ。考えてるんだからさー」
僕「ごめんごめん」
そうだよな、と僕は反省する。
時間を限られているわけじゃないし、授業をやってるわけでもない。
何かおもしろいことはないかな、と探しているんだから先を急ぐ必要はまったくないんだ。

ユーリ「この $r = \theta$ という式が、 極座標だとどんな図形を表しているかってことだよね? でもさー……この $r$ は長さだけど、 $\theta$ は角度じゃん? 長さと角度が等しいってどゆこと?」
僕「うん。 $r$ は動径。 この $r$ は、平面上に定めた極という一点からの距離を表している。ユーリの言うとおり、長さだね」
ユーリ「だよね」
僕「それから $\theta$ は偏角で、極から伸びた始線と呼ばれる半直線と動径がつくる角の大きさを表している。ユーリの言うとおり、角度だよ。 たいていはラジアンで考えるけれど、いまは度で考えている」
極座標の基本的アイディア(再掲)
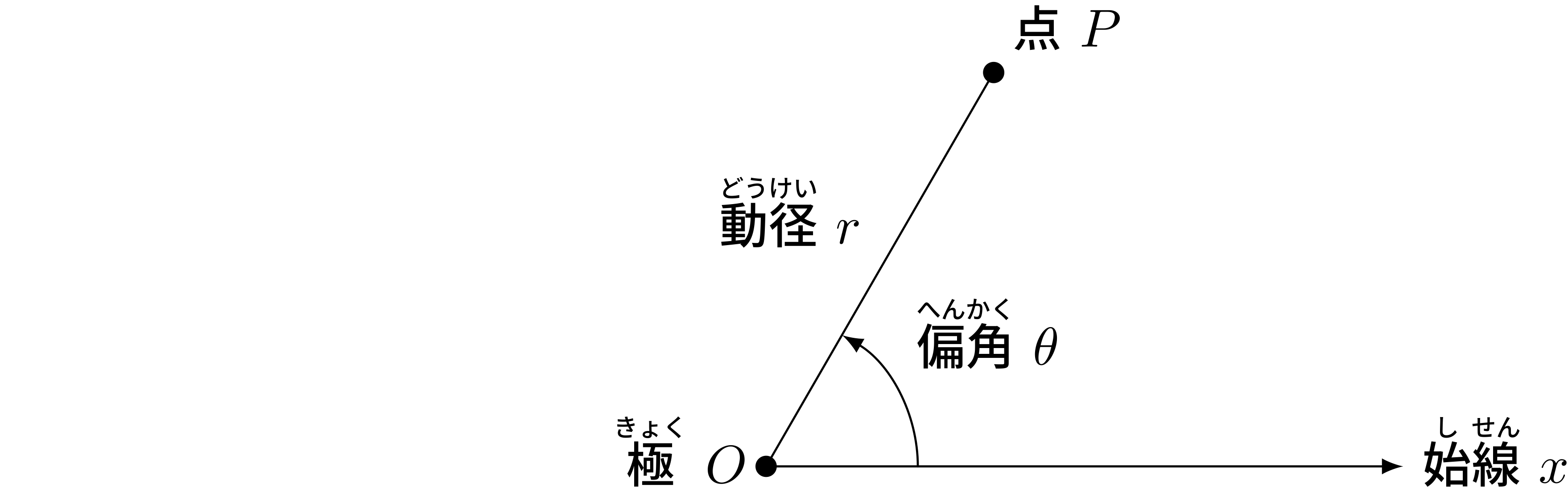
平面上に極と呼ばれる点 $O$ を決めます。
極から伸びる始線という半直線 $x$ を一つ定めます。
平面上の任意の点 $P$ に対して次のように $r$ と $\theta$ を定めます。
そして、動径 $r$ と偏角 $\theta$ の組、
$$ (r, \theta) $$ で点 $P$ を表すことにします。
ユーリ「でしょでしょ? $r = \theta$ だと、長さと角度が等しくなるよ?」
僕「ここでは、長さも角度も数として考えてほしいな。 $r$ はセンチメートルでもミリメートルでも何でもいいけど、ある単位で考えた長さを表す数。 それから $\theta$ の方は、度で考えた角度を表す数。 そう考えることにすれば $r = \theta$ という式の意味はわかるよね」
ユーリ「んー……そっか。たとえば角度が $90$ 度のときは、動径の長さは $90$ cmとか、そういうこと? $90$ cmってデカい図になっちゃう!」
僕「そういうこと。 $90$ cmが大きすぎるなら $90$ mmでもいいよ。とにかく単位を決める。 いまユーリが言った例は、 $r = \theta = 90$ の例だね。つまり、この点は、 $r = \theta$ が表している図形上にある一点といえる」
$r = \theta = 90$ の点

ユーリ「$90$ がそこなら、 $180$ は……あっ! わかったわかった。ちょっと待って! $r = \theta$ の図形、わかりそう! 紙ちょーだい!」
僕はユーリにコピー用紙を渡した。
机の上にはいつもコピー用紙の束が置いてあって、好きに使えるようにしてあるのだ。
彼女は嬉々として図を描いている。
僕「どう?」
ユーリ「こんな……こんな感じ? ちょっとぐちゃっとしたけど、こーゆー渦巻きになるんじゃない?」
ユーリが描いた渦巻き

僕「すごい! よく一気にここまで行ったねえ!」
ユーリ「ふふん。あのね、聞いてよ」
僕「聞いてるよ」
ユーリ「$r = \theta$ が表す図形って、 $90$ 度回ったところだと $r = 90$ になるわけでしょ? だったら、 $180$ 度なら $r = 180$ で、 $270$ 度なら $r = 270$ になる。 $360$ 度なら $r = 360$ だから、 $90$ 度進むごとにひと目盛りずつ進むじゃん?」
僕「そうだね。ユーリが縦横に引いた直線に描いた目盛りのことだね。ひと目盛りが $90$ で、だんだん極から遠ざかっていく」
$r = \theta = 0,90,180,270,360$ の点
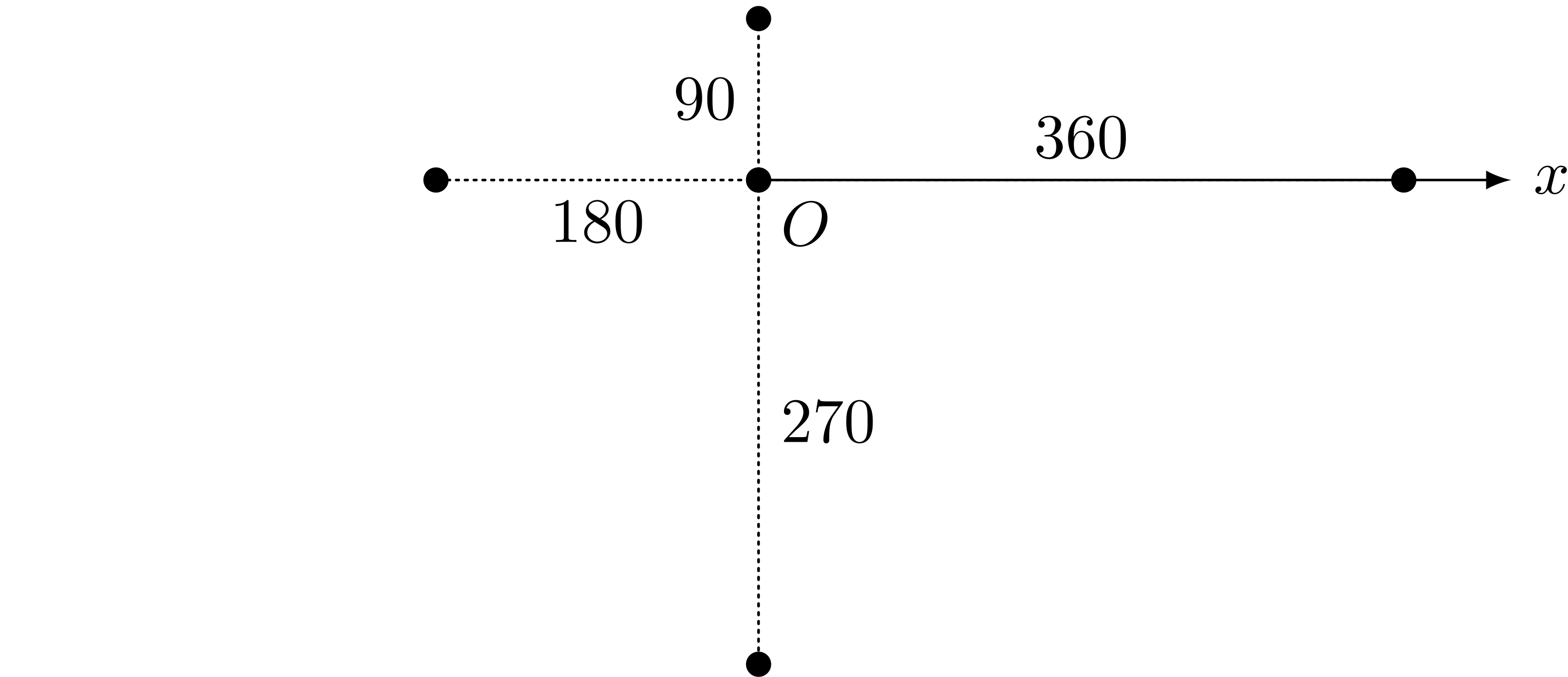
ユーリ「そーそー! だからその点を通るように考えると、さっきの渦巻きになる」
僕「$45$ 度単位で点を打つとこうなるよ」
$r = \theta = 0,45,90,135,180,225,270,315,360$ の点
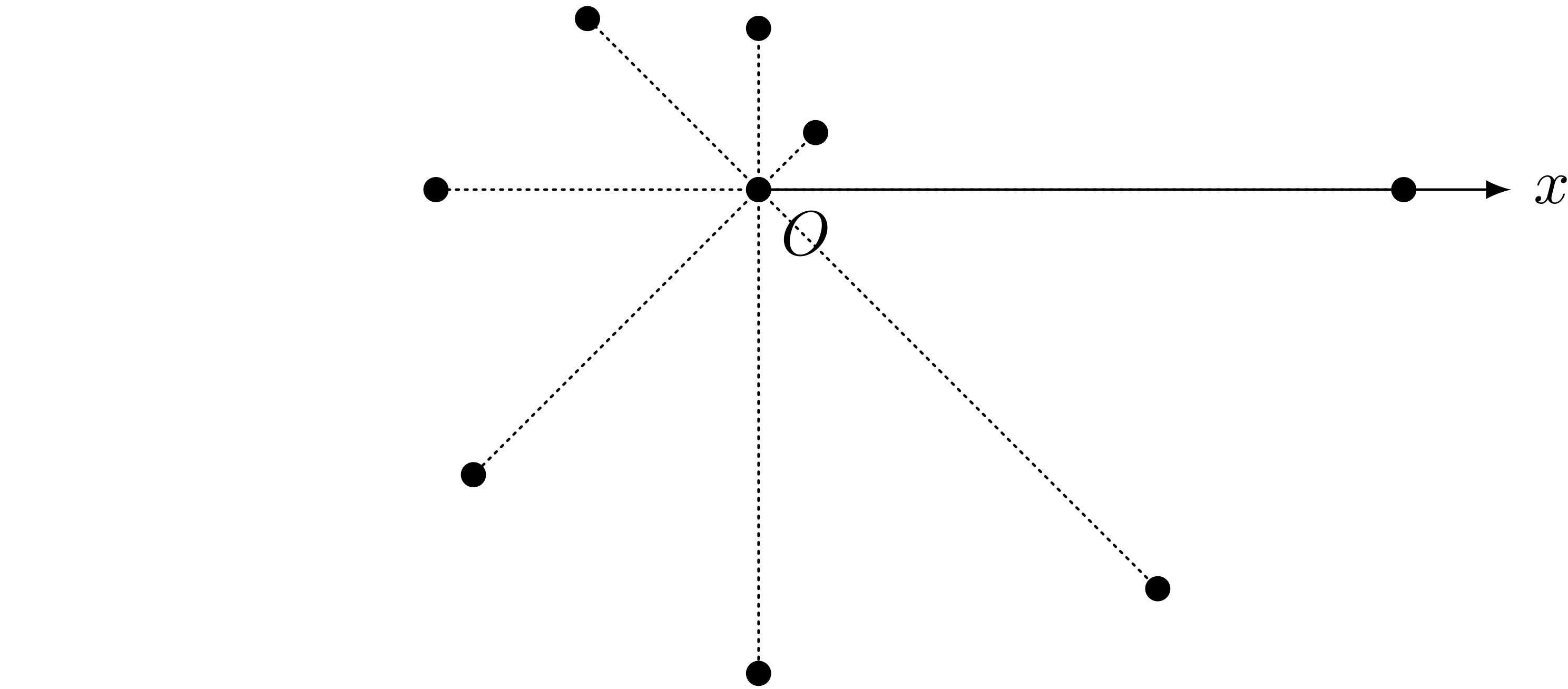
ユーリ「たーのーしー!」
僕「そして、滑らかにつなぐとこうなる。これはアルキメデス・スパイラルと呼ばれている曲線になる」
アルキメデス・スパイラル $r = \theta$ $(0 \LEQ \theta < 360)$
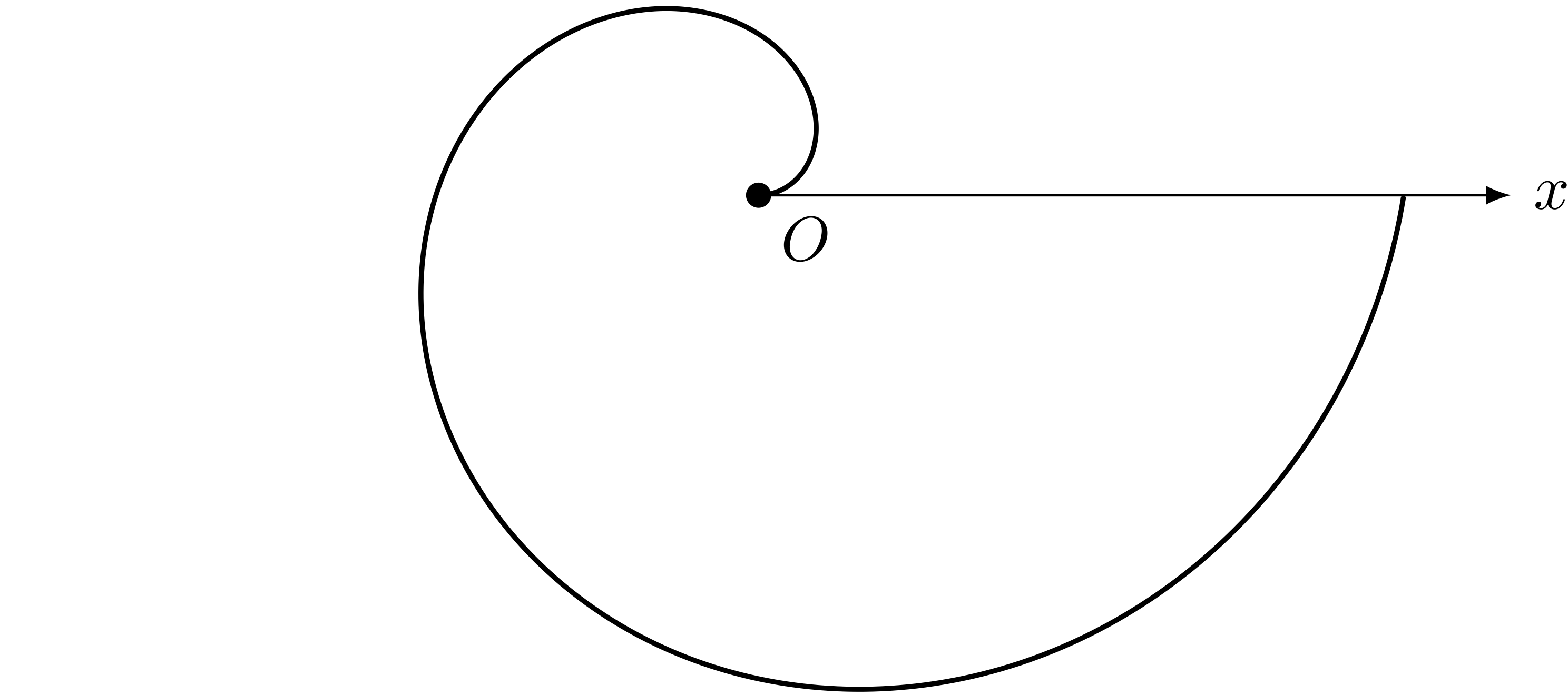
ユーリ「アルキメデス・スパイラル! 何それカッコイイ名前!」
僕「アルキメデス螺旋ともいうね」
ユーリ「$r = \theta$ だから、偏角 $\theta$ が大きくなればなるほど、動径 $r$ も大きくなってく。 だからひゅわ〜っと長くなってくんだね。 これ、もっとずっと続けられるでしょ? ぐるぐるっと」
僕「そうだね。たとえば二回転するとこんな感じになる。巨大になりすぎるから全体の縮尺を半分にしたけど」
アルキメデス・スパイラル $r = \theta$ $(0 \LEQ \theta < 720)$
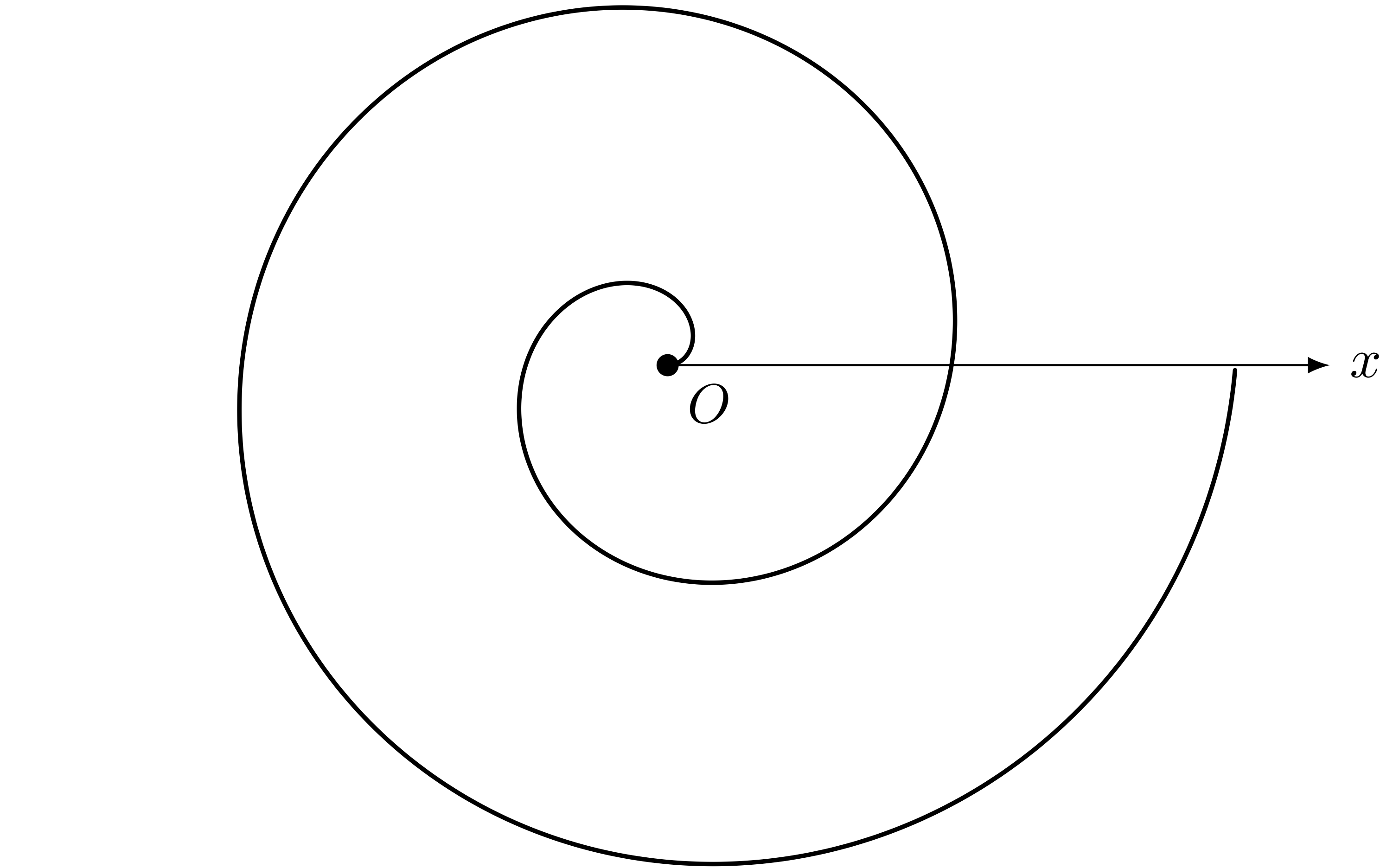
ユーリ「もっとじゃんじゃん回そうよ」
僕「たとえば、十回転すると……こうなる」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2022年7月22日)