![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ここは僕の部屋。
僕とユーリは、与えられた立方体の二倍の体積を持つ立方体を作図する問題(立方体倍積問題)に取り組んでいた(第355回参照)。
立方体倍積問題
定規とコンパスを有限回だけ使って、 与えられた立方体の二倍の体積を持つ立方体を作図してください。

僕たちは数学史の本を《予言者読み》しながら、いにしえの人たちの考えに触れようとしている。
《予言者読み》というのは僕の命名で、数学の本を少しずつ読み進め、 その時点まで読んできたことをヒントにして、本の先に何が書いてあるのかを読む前に言い当てるという読み方のことだ。 ちょっとゲーム風でもある。
ユーリ「本の《予言者読み》たーのしー! どんどん行こー!」
僕「じゃあ、また少しずつ読んでいくことにするよ」
僕たちはここまで、メナイクモスの解法を《予言者読み》してきたところだ(第356回参照)。
引き続き、数学史の本に紙を乗せ、それをずらしながら少しずつ読み進めた。
紙を乗せているのは、先の記述がうっかり目に入るのを防ぐためだ。
ユーリ「おっ、おもしろそーな話が出てきたよん」
僕「どれどれ……」
エウトキオスの注釈
さて、アルキメデスの著作『球と円柱について』に対してエウトキオスが書いた注釈の中には、 立方体倍積問題の「解法」を集めたものが含まれていた。
ユーリ「どーする?」
僕「いやいや、どうしようもないよ。歴史的な事実だけから先読みをするのは無理。 何か数学的な話が出てきたところで止めることにしないと。 エウトキオスという人が、立方体倍積問題の解法を集めたという話からは何もわからない」
ユーリ「そりゃそーか。あっ、でも、この後に立方体倍積問題の解法がいろいろ出てくることはわかるよ!」
僕「そうだね……といっても、 立方体倍積問題が定規とコンパスを有限回使うだけでは解けないことは証明されている。 だから、歴史的に数学者が挑戦してきた様子が書かれているんだろうな」
ユーリ「メナイクモスの解法みたいに? (第356回参照)」
僕「うん……そういう意味では確かに、数学的な内容でなくても《予言者読み》はできるな。 次に何が書かれているかを予想しながら読んでいくんだ」
ユーリ「ミステリーみたい」
僕「じゃあ、続けて読んでいこう。ミステリーツアーだ」
エラトステネスの解法
二つの比例中項を求めるエラトステネスの解法では、次の道具を使い、 与えられた $a,b$ に対して $a:x = x:y = y:b$ を満たす $x,y$ を求める。
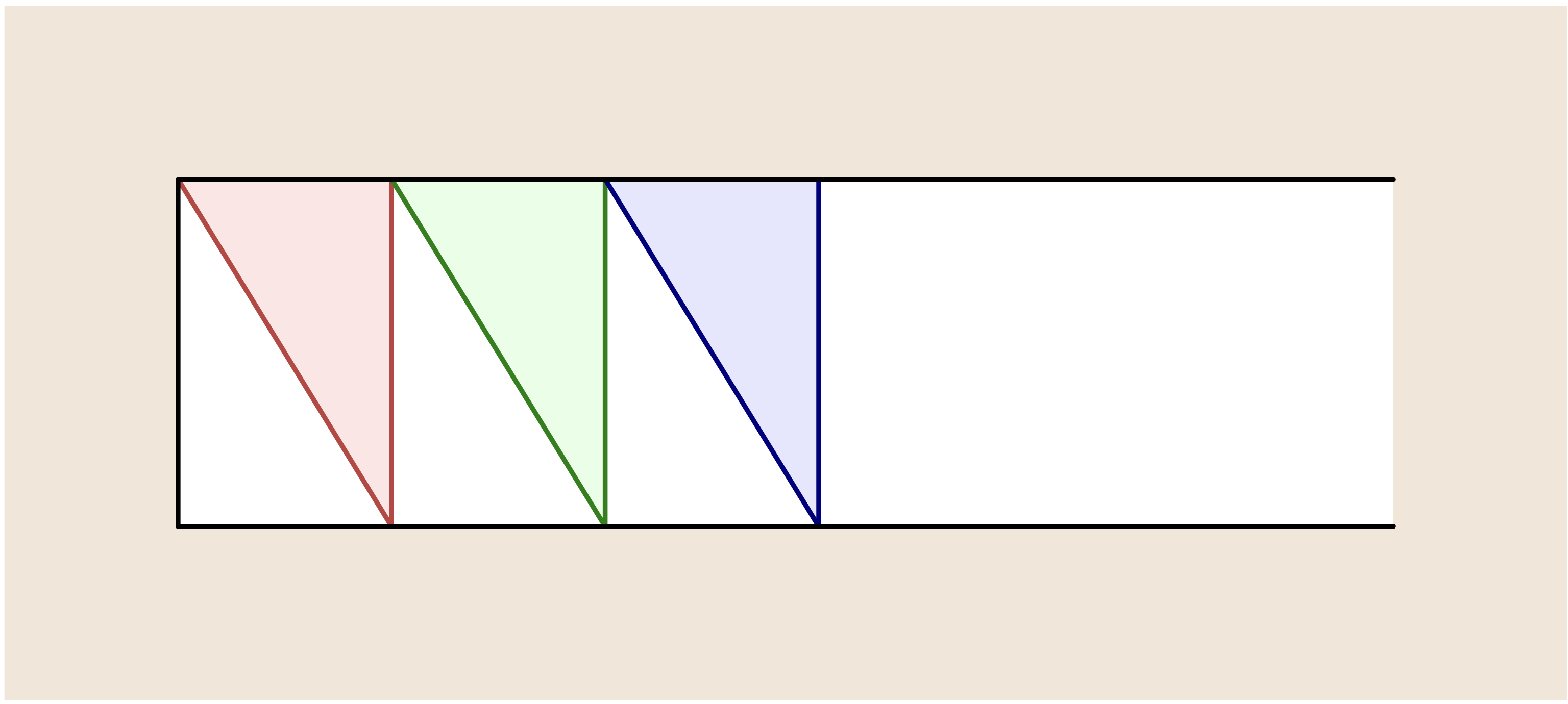
僕「おっ!」
ユーリ「見えちゃった!」
僕「図が先に出てきたね……エラトステネス?」
ユーリ「三角形がたくさん出てきた。これで二つの比例中項がわかるの?」
僕「そうなんだろうなあ。 ヒオスのヒポクラテスが見つけた二つの比例中項を求めさえすれば、 当時の未解決問題だった立方体倍積問題が解けることになる(第355回参照)わけだからね」
ユーリ「うんうん」
僕「でも、この図だけじゃ、さすがに何も考えられないよ。先を読むか。 ところで、ここに書いてあるエラトステネスは、あのエラトステネスかな?」
ユーリ「ほほー、お知り合いですか? そのエラ……エラトスト……ストネ?」
僕「そこは噛まずにスッと言ってほしかった。エラトステネス」
ユーリ「エ・ラ・ト・ス・テ・ネ・ス!」
僕「確かに、ギリシャの人の名前は言うのが難しいときがあるけどね。 エラトステネスというと、素数を求めるエラトステネスの篩(ふるい)が有名だね」
ユーリ「ふるい?」
僕「$2,3,4,\ldots$ と数を並べておき、小さい方から順番に倍数を消す。 そうやって、ふるいにかけるようにして素数を見つけていく方法だよ(『数学ガールの秘密ノート/整数で遊ぼう』参照)。 与えられた数が素数かどうかを判定する方法といってもいい」
【CM】
テトラ「お話の途中ですが、お知らせです。 素数のこと、倍数の見分け方、数当てクイズ、謎のパズル《ぐるぐるワン》など、整数で遊ぶ楽しい話題がいっぱいの本、『整数で遊ぼう』はこちらです!」
テトラ「『整数で遊ぼう』から、エラトステネスの篩の図を引用しますっ!」
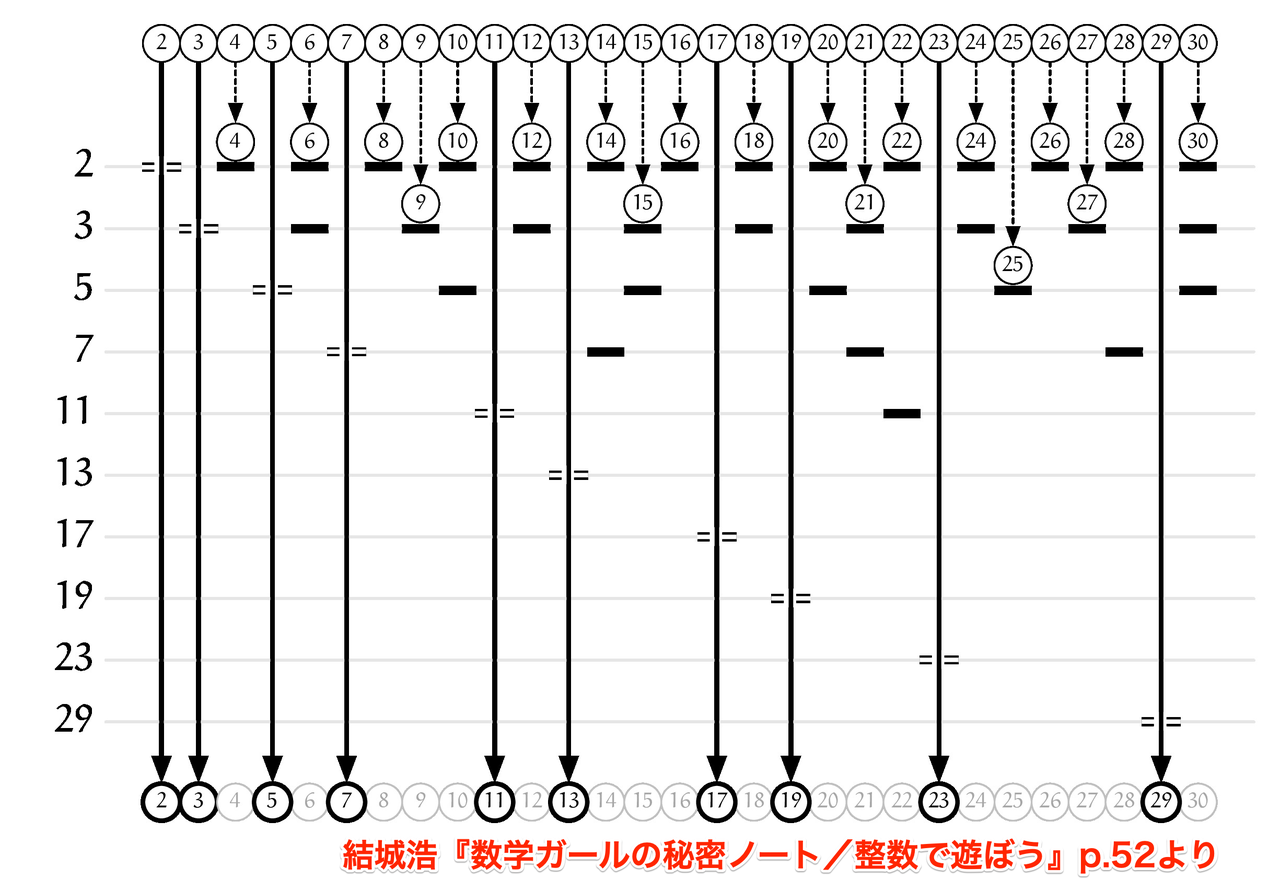
ユーリ「テトラさんのCM、ひさびさ」
僕「それから、地球の大きさを初めて測ったのもエラトステネスだよ。紀元前に地球の大きさを測っていたというのはすごいよね」
ユーリ「は? そんなに昔からロケットがあったの?」
僕「違う違う。太陽の光が作る影を利用して、地球の大きさを計算したんだ」
ユーリ「影で地球の大きさがわかるって、ぜんぜん意味わかんない」
僕「最初に考えるのはすごく難しいと思うけど、わかってしまえば簡単だよ。こんな図を描けばすぐわかると思う」
エラトステネスが地球の大きさを測る方法の原理図
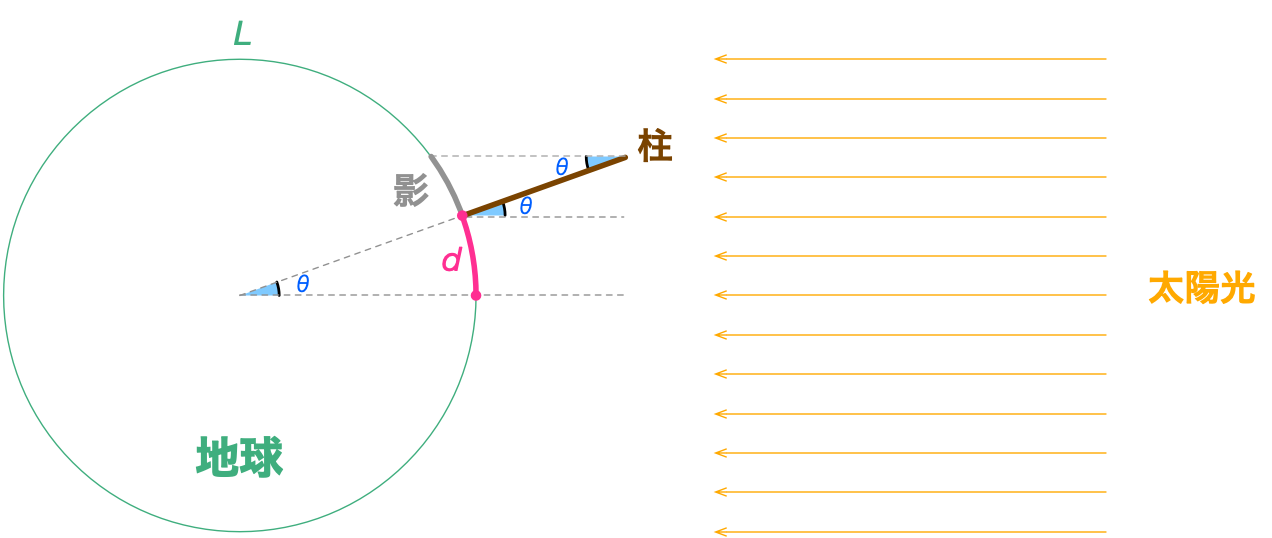
ユーリ「この大きな円が地球だよね……右上に向かって立ってるのが柱? 地球に比べると、すごく巨大な柱ですこと(にやにや)」
僕「わかって言ってるね。もちろんこの柱は説明のために長く描いているんだよ。 注目するところはこの角度 $\theta$(シータ)だ。この角度は、柱の長さが長くても短くても変わらない」
ユーリ「ほほー……柱がどれだけ傾いているかってことだよね」
僕「そうだね。柱の先端と影の先端を使えば、柱の傾き具合を表す角度 $\theta$ がわかる」
ユーリ「ふむふむ」
僕「太陽がちょうど真上にあるタイミングで、そこから距離が $d$ だけ離れたところで $\theta$ を測る。 角度は $\theta$ 度だとしよう。地球が円だと考えて、その円周の長さを $L$ とすると、 $360$ 度で一回りすることから、 $$ \frac{d}{L} = \frac{\theta}{360} $$ になることがわかる。つまり、 $$ L = \frac{360d}{\theta} $$ となって $d$ と $\theta$ から $L$ がわかる。 もちろん、 $\theta$ をラジアンにしても同じ。そのときは計算の $360$ の代わりに $2\pi$ を使うことになる。 いずれにしても、この $L$ が地球のまわりの長さになるわけだ」
ユーリ「あったまいー!」
僕「ここでエラトステネスが使った条件がうまいよね」
ユーリ「条件って何?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2022年5月13日)