![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ここは僕の部屋。
僕とユーリは、与えられた立方体の二倍の体積を持つ立方体を作図する問題(立方体倍積問題)に取り組んでいた(第355回参照)。
立方体倍積問題
定規とコンパスを有限回だけ使って、 与えられた立方体の二倍の体積を持つ立方体を作図してください。

僕たちは数学史の本を《予言者読み》している。
《予言者読み》というのは僕の命名で、数学の本を少しずつ読み進め、 その時点まで読んできたことをヒントにして、本の先に何が書いてあるのかを読む前に言い当てるという読み方のことだ。
ユーリ「立方体倍積問題の次の解法は?」
僕「新たな登場人物が出てきたよ。アルキュタスだ」
アルキュタス
アルキュタスは、ピタゴラス学派の一人で、哲学者プラトンの友人であった。
彼は多くの秀でた能力を持っており、 哲学者でもあり、政治家でもあり、将軍の仕事も七年務めた。
数論では平均に関わる研究を行い、音楽では弦の音程に関する比についても研究した。
メナイクモスはアルキュタスの教え子である。
機械を作ることにも通じ、アルキュタスは、木製でできた機械仕掛けで空を飛ぶ「鳩」を作ったと言われている。
ユーリ「何気にめっちゃすごいこと書かれてない? 機械仕掛けで空を飛ぶ鳩を作った!」
僕「すごいけど、これ以上の情報は書かれてないなあ。 それにしても、アルキュタスはいろんなことができた人なんだね」
ユーリ「そして、立方体倍積問題も……」
アルキュタスの解法
二つの比例中項を求めるアルキュタスの作図は、三次元的に行われる。
三つの立体面の交点として求める点を作図するからである。
三つの立体面とは、
である。
僕「この解法も、何だかすごそうだな」
ユーリ「三次元的ってどーゆー意味だろ」
僕「ここに書いてある通り、三つの立体を作って、その交点として二つの比例中項を求めるってことなんだろうと思うけど」
ユーリ「ふーん……トーラスってなに?」
僕「トーラスはドーナツの表面のような面だね。円柱はわかるよね」
ユーリ「円錐もわかるよ。でもその三つの交点って、さっぱりわかんない!」
ユーリの心の中のトーラス、円柱、円錐

僕「僕もまだわからないよ。 だって、立体の大きさや配置が決まらなければ交点だって決まらない。 アルキュタスの解法はこれらの三つの立体を作っていく手順を示しているはずだね」
ユーリ「手順?」
僕「だから、一歩一歩追っていけば、必ずその立体が作れるはず。そういう手順が次に書かれているはずだ。それは想像が付く」
ユーリ「立体を作る手順……折り紙の手順みたいなもん? お兄ちゃん、《予言者読み》してよ」
僕「具体的な手順を読み取るのはまだ無理だよ。でも言えることは、その手順の後で、確かにそれが二つの比例中項になっている、と示されているはず」
ユーリ「それっぽく決まるじゃなくて、バシッと決まる?」
僕「そうだね。じゃあ、次のページに進もう」
ユーリ「だーかーらー! 図が見えちゃうって言ったじゃん! パッと進めないでよー! 《予言者読み》してるんだからさー」
僕「ごめんごめん……でも、これは無理かも。この図の複雑さは……」
ユーリ「えっ、もーあきらめるの? 早すぎ! 『一歩一歩追っていけば、必ずその立体が作れるはず』っていったじゃん」
僕「了解、了解。そうだったね。さて、じゃあ、説明を読みながらこの図を解読していくか……」
ユーリ「未来を読み取る《予言者読み》じゃなくて、古代文字を読み解く《探険者読み》じゃのう……」
アルキュタスの解法(続き)
与えられた $a$ と $b$ に対して、 $a:x = x:y = y:b$ を満たす比例中項 $x,y$ を求める。
(1)線分ABの長さが $a$ で、直径ACの長さが $b$ になるような円を描いて、円周上に三点A,B,Cを定める。この円を円αと呼ぶ。また円αを含む平面を平面αと呼ぶ。
(2)線分ACを直径に持つ円βを新たに描く。ただしその円βを描く平面は、円αを含む平面αと垂直な位置関係にある。円βを含む平面を平面βと呼ぶ。
(3)円βを回転させてトーラスを描く。回転の軸となる直線は点Aを通り、平面αに垂直である。

僕「まずは、これまでと同様だね。立方体倍積問題に直接取り組むんじゃなくて、ヒオスのヒポクラテスが発見した二つの比例中項の問題に取り組んでる(第355回参照)」
ユーリ「うん」
僕「(1)から順番に読んでいこう。こういうときは先を急いじゃだめだ」
ユーリ「《探険者読み》はつらい……」
僕「与えられているものは $a$ と $b$ で、ここではその二つの数をもとにして円αを作っている」
ユーリ「(2)は円βだけど、ややこしいこと言ってるよ。平面αと垂直ってどゆこと?」
僕「あれ……この図には円βは描かれてないなあ。それから(3)のトーラスも描かれていない。これは……文章を読むだけじゃダメだね。図に書き込みしながら読んでいくことにしようか。ええと……」
(1)(2)(3)の解説図
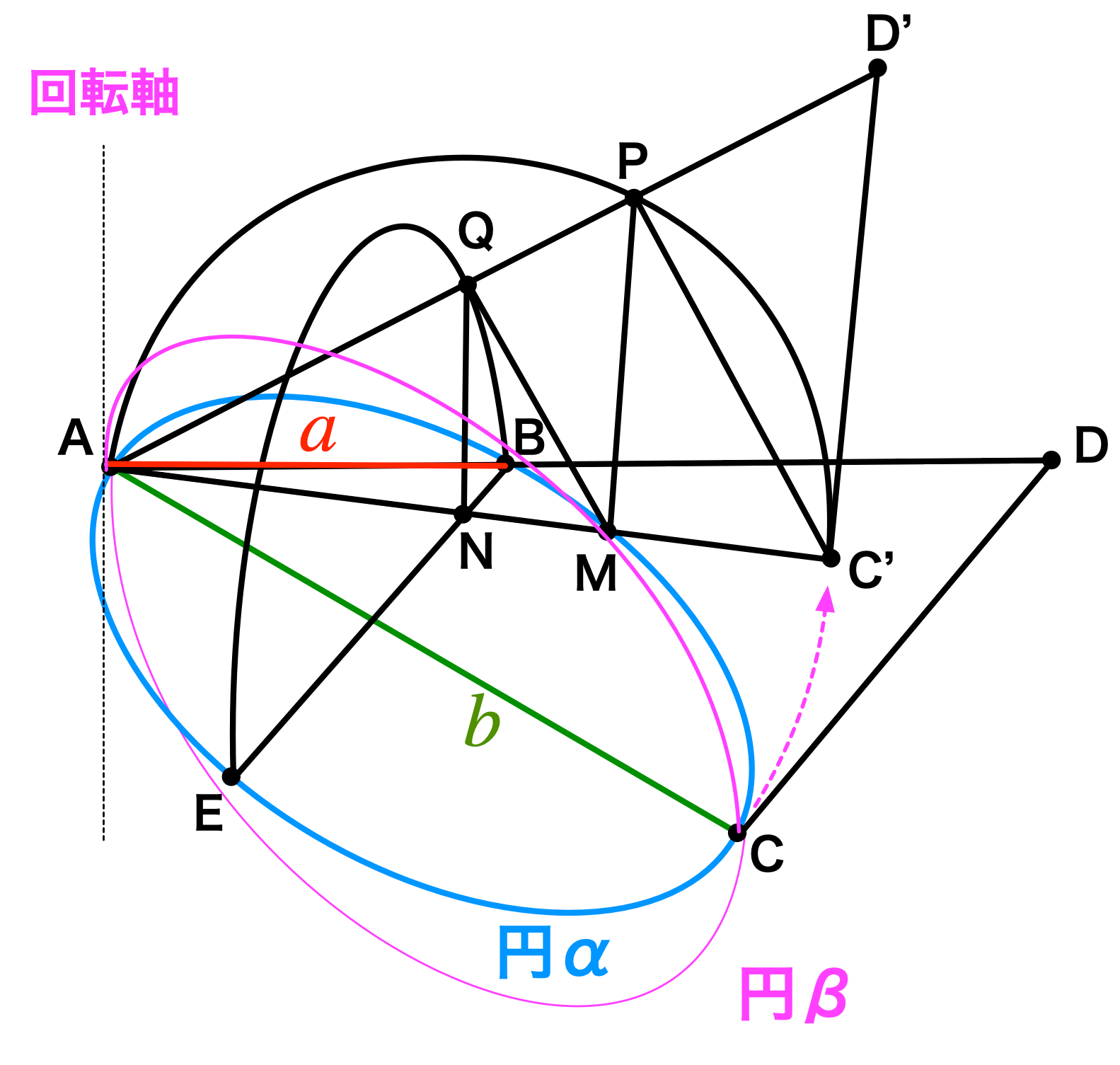
ユーリ「うわあ……すでにぐちゃぐちゃ」
僕「$a,b$ を描き入れて、円αをはっきりさせた。円αが楕円に見えるのは、斜め上から見てるためだね。そして、その円αに垂直に円βを描いた。 円αと円βは直径ACを共有していて垂直に交わっている。この円βを回転軸で回転させるとトーラスになる」
ユーリ「トーラスになる? ……ドーナツの穴、つぶれてるね」
僕「そうだね。円βが回転軸に接しているからね。ともかくここまでは解読できた。トーラスを描くともっとごちゃごちゃになるから、 心の中で描くことにしよう。想像できる?」
ユーリ「……なんとか」
ユーリの心の中のトーラス

アルキュタスの解法(続き)
(4)平面αに垂直で断面が円αとなる円柱を描く。この円柱の側面とトーラスとの交線は三次元空間上の曲線となる。
(5)円αの直径ACを軸とする円錐面を次のように作図する。 まず、平面α上で、円α上の点Cにおける接線を描き、線分ABを延長した直線との交点をDとする。 これでできる三角形ACDを、線分ACを軸にして回転させる。
(6)三角形ACDを線分ACを軸にして回転させたとき、線分AD上にある点Bが回転する軌跡は円を描く。その円を円γと呼ぶ。 円γと円αの二つの交点のうち、点Bではない方を点Eとする。線分BEは円γの直径である。
(7)円γの直径BEと、円αの直径ACは垂直に交わる。
僕「図に描きこんでいくと……こうかな」
(4)(5)(6)(7)の解説図
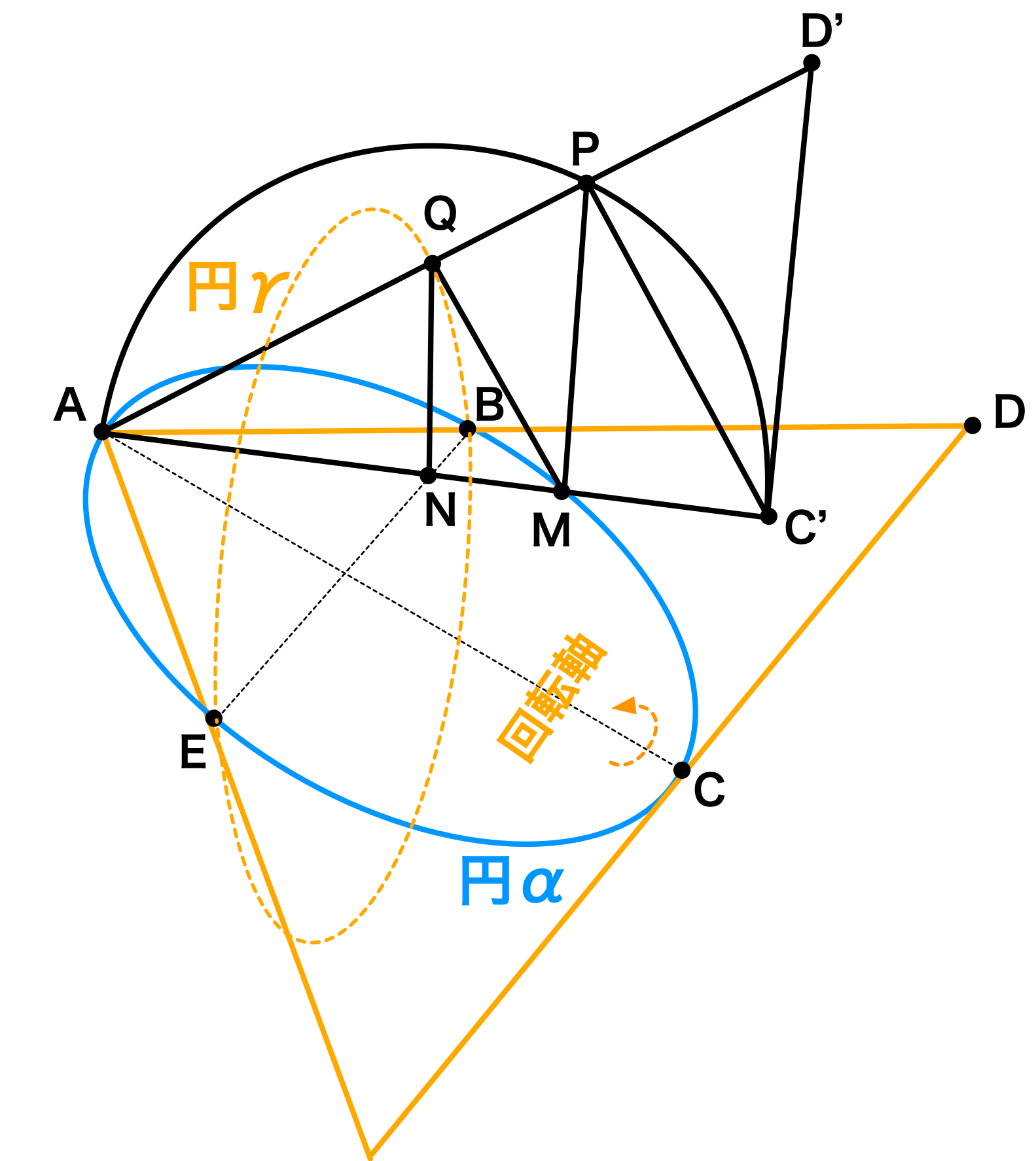
ユーリ「おお……」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2022年5月20日)