第355回 シーズン36 エピソード5

立方体倍積問題で《予言者読み》をやってみよう（前編）

僕の部屋

ユーリ「ねー、お兄ちゃん！」

僕「『なんか、おもしろい話、ないのー？』」

ユーリ「あっ、何それ。人のセリフ取るなよー！……って、ちょっと待って。何だか話がループしてない？」

僕「何のこと？」

ユーリ「このやりとり、こないだやったばっかじゃん（第351回参照）。タイムループものかと思った」

僕「タイムループ？　でもユーリはどうせ『なんか、おもしろい話、ないのー？』って言うんだろ？ ループを生み出しているのはユーリじゃないか」

ユーリ「そんなことないよー。 ねーお兄ちゃんは立方体倍積問題って知ってる？」

僕「うん、知ってるよ」

ユーリ「やっぱり知ってたかー……こないだの円積問題がおもしろかったから（第353回参照）、 とある知人に出題したんだよ。そしたら立方体倍積問題で逆襲された」

僕「とある知人……またボーイフレンドと《数学対決》してたんだ」

ユーリ「そーゆーんじゃないよ」

僕「立方体倍積問題は、こういう問題だよね」

ユーリ「そーそー」

僕「でも、これも円積問題と同じく不可能であることが証明されている問題だよね、確か」

ユーリ「これって、立方体を作るって言ってるけど、結局辺の長さを作る問題なんでしょ？」

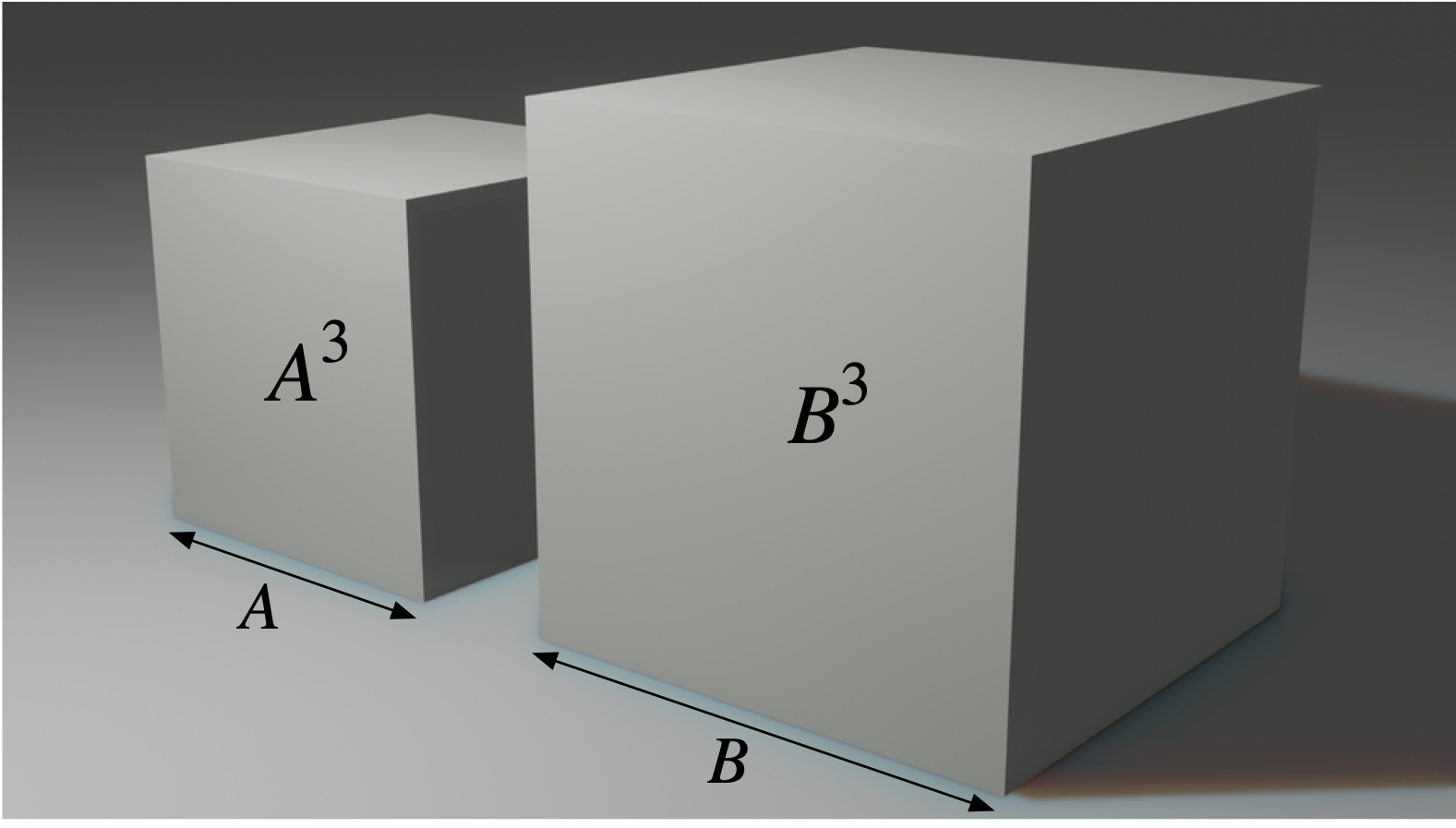
僕「うん、そうだよ。円積問題のときと同じだね。 だから、与えられた立方体の一辺の長さを $A$ とすると、 $$ B^3 = 2A^3 $$ を満たす正の実数 $B$ を求めればいいということになる」

ユーリ「ふんふん。 $A^3$ が与えられた立方体の体積で、 $B^3$ が求めた立方体の体積。 それで、 $B^3$ は $A^3$ の二倍になってるでしょっと」

僕「そうだね。ユーリは正しく読み解いているよ。 『立方体の体積』や『二倍の体積を持つ立方体』のような言い方をすると形についての表現、つまり幾何の表現になる。 でも、 $$ B^3 = 2A^3 $$ という書き方をして式で表せば、代数や解析の表現になる」

ユーリ「こんくらい、手慣れたもんよ」

僕「ところで、 $A$ が与えられたときに $B^3 = 2A^3$ を満たす $B$ を求めるということは、 $$ X^3 = 2 $$ を満たす $X$ を求める方程式を解く問題だと思ってもいい。つまり立方体倍積問題は、 三乗したら $2$ になる問題を求める問題になる。言い換えれば $2$ の三乗根を求める問題だと考えられるんだ。 $2$ の三乗根は三つあって、そのうちの実根を求める」

ユーリ「$2$ の三乗根？　またややこしいこと言い出したね？」

僕「いま $A$ が与えられていて $B^3 = 2A^3$ を満たす $B$ を求めたい。 でも、もしも $X^3 = 2$ を満たす $X$ があったら、その $X$ に $A$ を掛ければそれが求めたい $B$ になる……という話」

ユーリ「$X$ に $A$ を掛けたのが $B$ ってことは、 $$ B = XA $$ だから……三乗すると、 $$ B^3 = (XA)^3 = X^3A^3 $$ になるけど、もしも $X^3 = 2$ が成り立つとしたら、 $$ B^3 = 2A^3 $$ ってことだから、結局 $AX$ が二倍の体積を持つ立方体の一辺になる」

僕「その通り」

ユーリ「ふーん……てことは、 $2$ の三乗根は存在しないってことなの？」

僕「いやいや、実数の中に $2$ の三乗根は存在するよ。そのことは $y = x^3$ という曲線のグラフと、 $y = 2$ という直線の交点を考えればわかる。交点の $x$ 座標は $x = \sqrt[3]{2}$ になるから」

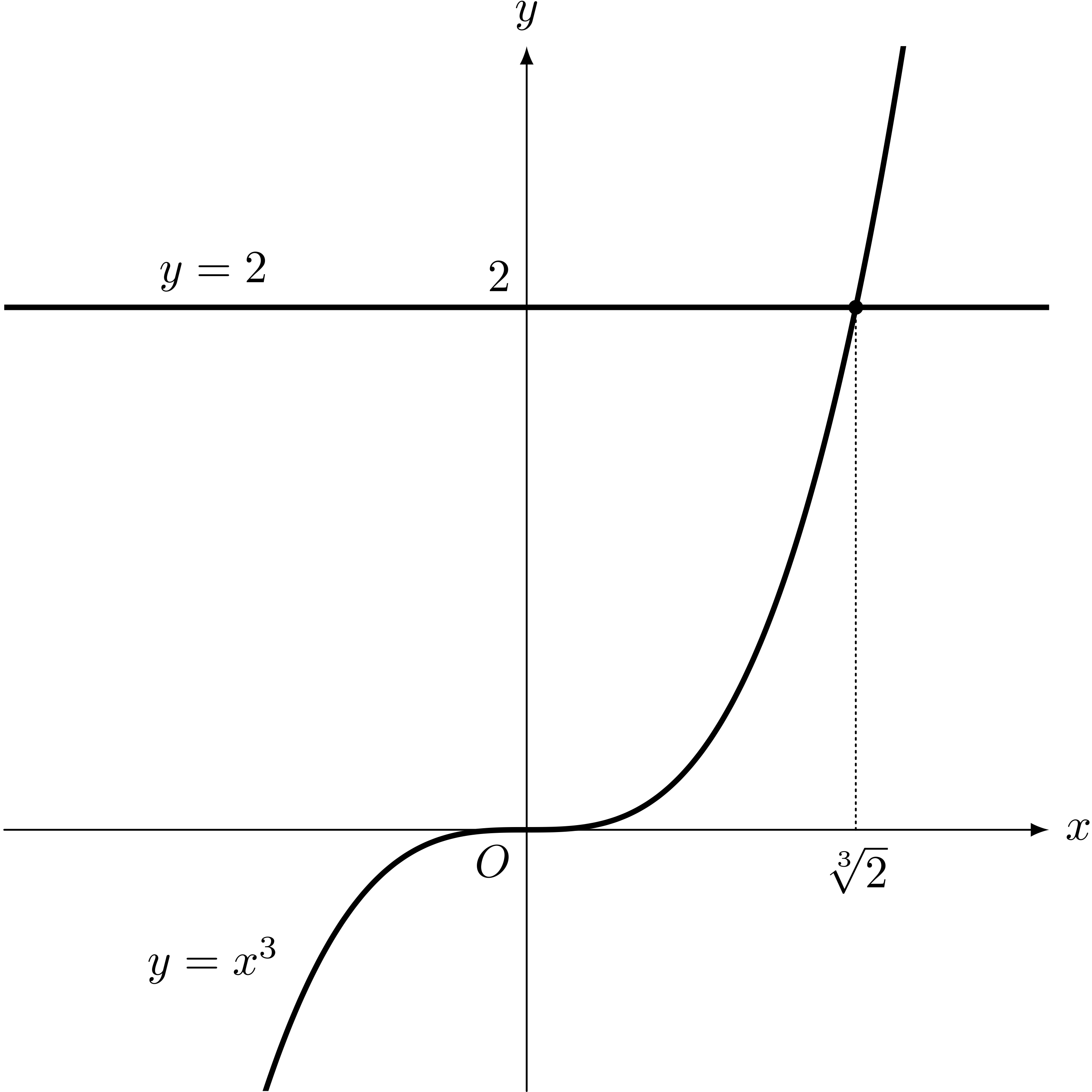
ユーリ「ふむー」

僕「実数の中に $2$ の三乗根は存在する。 でもいまは、定規とコンパスを有限回使って作図できるかどうかを考えている。 そういう制約を付けてしまうと、 整数の四則演算と平方根を取る演算を繰り返すだけでは $2$ の三乗根は得られない」

ユーリ「お兄ちゃん、詳しいね」

僕「詳しくないよ。立方体倍積問題には何か歴史的逸話があったと思うけど、 そっちの方はもう忘れてしまった」

ユーリ「何か本ないの？　それともネットで調べる？」

僕「あるある。ちょっと待って。図書館から借りてきて、まだ読んでない本だけど……」

ユーリ「これも、読んだらつまらない？」

僕「何のこと？」

ユーリ「自分で考える前に、答えを調べちゃったらおもしろくないって言ってたじゃん」

僕「それは数学の問題の話だろ？　数学の問題を少しも考えずに検索したら、答えを見てしまう。 答えをそうやって知ってしまったら、答えを知らない状態には戻れない。だから、せっかくの考えるチャンスをなくしてしまう……でも、 歴史的な話を調べるのは別にかまわないよ。歴史的逸話を自分で考えるわけにはいかないんだから」

ユーリ「あはは」

僕「この本の索引を見て、『立方体倍積問題』を調べて……あった。 立方体倍積問題にはこんな伝説があるという話。これが本当の話かどうかはわからないけど、言い伝えがある」

ユーリ「へー……すっごく理不尽なお告げ！」

僕「確かにそうだね」

ユーリ「一つの辺を二倍にしたら、立方体じゃなくなっちゃうじゃん！」

僕「まさに」

ユーリ「辺を全部二倍にしたら、体積は八倍になっちゃう！」

僕「そうだね。 $(2A)^3 = 8A^3$ だから、体積は八倍になる。 このデロス島の伝説から、立方体倍積問題をデロスの問題とも呼ぶ、と書いてあるね。 だから結局、人々はこのお告げを満たすような祭壇を作れなかったことになる。立方体倍積問題は不可能が証明されているから」

ユーリ「ちょっと待って。 アポロンからのお告げには『定規とコンパスを有限回使うことしかできない』って条件があったの？　数学のテストみたいなお告げ……」

僕「いや、その条件のあたりがどうなっていたかまでは、この本に書いてないな」

ユーリ「だって、 $2$ の三乗根は存在するんだから、条件がついてないんだったら、その大きさの立方体を何とかして作ればいーじゃん！」

僕「それは確かにユーリのいう通り。ただ、作った後に証明しないといけないけどね」

ユーリ「何を証明すんの？」

僕「作図法は『何となくそのくらいの大きさになりました』……じゃダメで『ぴったりその大きさになりました』と言う必要がある」

ユーリ「そりゃそーだ」

僕「だから作図法は、技能の問題じゃなくて論証の問題なんだよ。なぜ、その作図法だと $2$ の三乗根になるかを言わなきゃいけない。証明だね」

ユーリ「ははーん。 理由が大事ってことだね。 『理由は大事……大事です $\NONA$』」

僕「ノナちゃんの真似やめい。……この数学史の本で立方体倍積問題の話がまだ続いてるから、先を読んでみよう」

ユーリ「ひぽくらてす、また出てきた。手がかり？」