![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ユーリ「コンデンサもおもしろいね!」
僕「そうだね」
ユーリ「ぜんぶバシッと決まるとこがおもしろい」
僕「へえ……」
ユーリ「何てゆーのかなー、リクツが合ってるじゃん?」
僕「そうだね。 《自然》ってすごいと思うよ。《法則》があるってことがすごい」
ユーリ「自然?」
僕「オームの法則だって、クーロンの法則だって、自然の法則だよね」
ユーリ「自然……?」
僕「自然っていったのは、この宇宙のことだよ。 この宇宙、そしてそこに存在するものが持っている性質を調べたり、確かめたり、わかっていることを理論にしたり、生活に応用したり……それが科学だよね。 物理学も、化学も、地学も、天文学も、生物学も……とにかくそういうものはぜんぶ自然科学だ。 科学は自然とかけ離れて存在するわけじゃないよ」
ユーリ「んー……《自然》ってゆーと、《緑がいっぱいで気持ちがいい森》みたいなイメージある。エコとか」
僕「そういう気持ちのいい《自然》もあるけど、台風みたいな恐い《自然》もあるよね」
ユーリ「そっか。自然は人間の都合を考えないもんね」
僕「科学もそうだよ」
ユーリ「えっ? 科学は人間が考えたものじゃないの? 人間に役立つように」
僕「うん。科学は人間が考えたものだよ。人間に役立つようにね。 科学は、もちろん人間を幸せにしてほしい。でもそのためにこそ、正しさを追求するときには、人間の『想い』とは関係なく考える必要があると思うな」
ユーリ「は? どゆ意味?」
僕「人間の『想い』とか『感情』で、正しさをねじまげてはいけないってこと。 どんな理論でも、実験で検証する。実験で確かめ、論理的に矛盾がないかを調べる。 科学的な正しさを支える実験では、人間の感情が邪魔になることがありそう」
ユーリ「えー……そーかなー」
僕「ユーリはそうは思わないの?」
ユーリ「科学者って熱心に研究してるんじゃないの? 役に立つすごい発見をしようって」
僕「そうだろうけど、その熱心さが何に向かうかが問題。 このあいだ読んだ本にはこんなことが書いてあったよ」
私は、どんな年齢のどんな科学者に対しても、 次の言葉以上にいい助言を与えることはできない。 すなわち、ある仮説を真であると信じる気持ちの強さは、 それが真であるか否かには何の関係もない。
ユーリ「こういう実験結果になれ! と熱心に考えても、そんなの関係ないぞっと」
僕「そういう話。自然は、人間の想いや熱心や感情とは関係なく動いている。 だから、こういう仮説が成り立ってほしい!……と思っても、自然は知ったことではない。 人間が、熱心さのあまりに、実験結果を誤認してはまずいよね」
ユーリ「そりゃまずいけど……」
僕「人間の気持ちで結果を誤認したら、自然を正確に理解できない。 そうするといざ科学を役立てようと思ったときに、 そこにあるのは役に立たない知識ってことになっちゃう」
ユーリ「確かに」
僕「人間の思惑で実験結果を動かしちゃいけない。思惑で動かさないからこそ、自然科学が役に立つんだ。そこがすごいところ」
ユーリ「誰がボールを投げても放物線を描く?」
僕「その通り! 人間の思惑とは関係なく、法則があるのがすごい」
ユーリ「法則……クーロンの法則とか、オームの法則とか」
僕「そうそう」
ユーリ「抵抗の並列つなぎと、コンデンサの直列つなぎが似てるの、おもしろいよね(第334回参照)」
僕「そうだね」
ユーリ「へへー……もうコツがわかっちゃったんだ」
僕「コツ?」
ユーリ「《共通のもの》と、《足し算になるもの》を見つければいいの」
僕「ああ、そうだね。《共通のもの》と《和になるもの》は、抵抗の並列つなぎでいうと……」
合成抵抗(並列つなぎ) (第332回参照)
二つの抵抗器があって、並列につなぐ。
抵抗値はそれぞれ $R_1, R_2$ とする。
抵抗を流れる電流をそれぞれ $I_1, I_2$ とする。
抵抗に掛かる電圧はどちらも $V$ である。
合成抵抗の抵抗値を $R$ とする。
全体の電流を $I$ とする。
このとき、 $$ I = I_1 + I_2 $$ が成り立つから、オームの法則より、 $$ V/R = V/R_1 + V/R_2 $$ が成り立つ。両辺を $V$ で割って、 $$ 1/R = 1/R_1 + 1/R_2 $$ を得る。
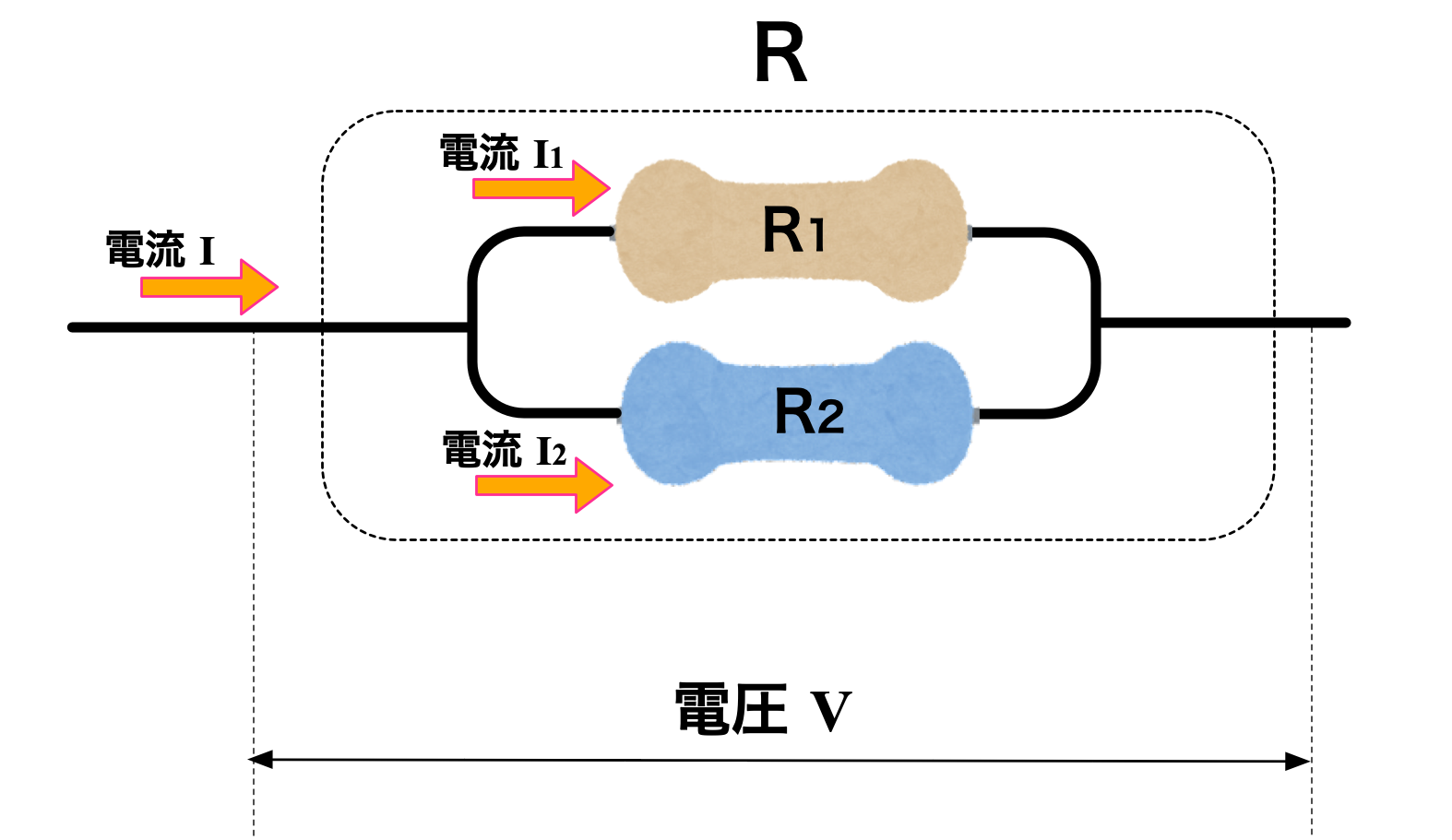
※図は「いらすとや」さんのイラストを加工して作成しました。
ユーリ「二つの抵抗に掛かる電圧は、合成抵抗と《共通》になってるし、二つの抵抗を流れる電流を足したのが、合成抵抗の電流になってる。 あとはオームの法則で一発」
僕「すごいな」
ユーリ「100%理解してるよん!」
僕「すごいすごい。じゃあね、こんなクイズはどうだろう」
クイズ
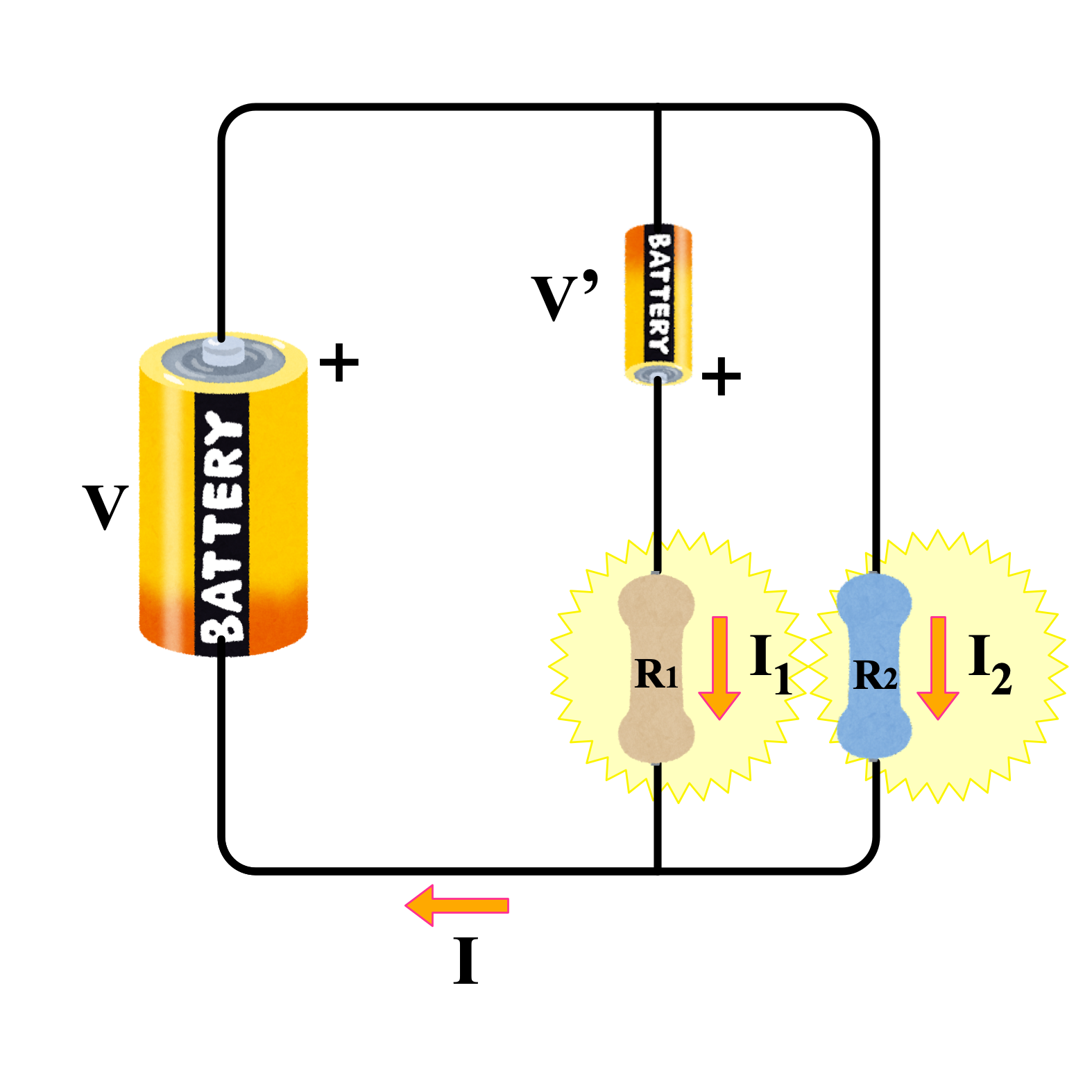
図のような回路があります。

このとき、電流 $I$ の大きさを求めてください(単位はアンペア)。
※注意: 実験には常に危険が伴います。 もしも電気回路を実際に作ってみようと考えるなら、 必ず指導者の監督のもとで行ってください。
ユーリ「カンタン! だって抵抗の並列つなぎだもん……違うーっ! 電池が二つあるのかーっ!」
僕「理科で習うよね」
ユーリ「やったよーな気もする。式を立てて計算した」
僕「そうそう。出てくる部品は電池と抵抗だけだから、そんなに難しくはないよ。考えるものは電圧と電流だけだし」
ユーリ「そっか……紙、ちょうだい!」
僕「何を計算すればいいかはわかるよね?」
ユーリ「わかる。 $I$ でしょ?」
僕「そうだね。 $V,V',R_1,R_2$ を使って、 $I$ を求める」
ユーリ「ヘィヘィ、アイを求めていきますぞっと……」

僕「……どう?」
ユーリ「むずい! あのね、この《片方にだけ入ってる電池》がじゃま。 $V'$ がすごくじゃま!」
僕「じゃまと言われてもね。どういうふうに考えたの?」
ユーリ「電流はすぐわかった。抵抗 $R_1,R_2$ に流れる電流を、 $I_1,I_2$ にするじゃん? そうしたら、必ず $I_1 + I_2 = I$ になるはず!」
$I_1 + I_2 = I$ になるはず
僕「それはどうして?」
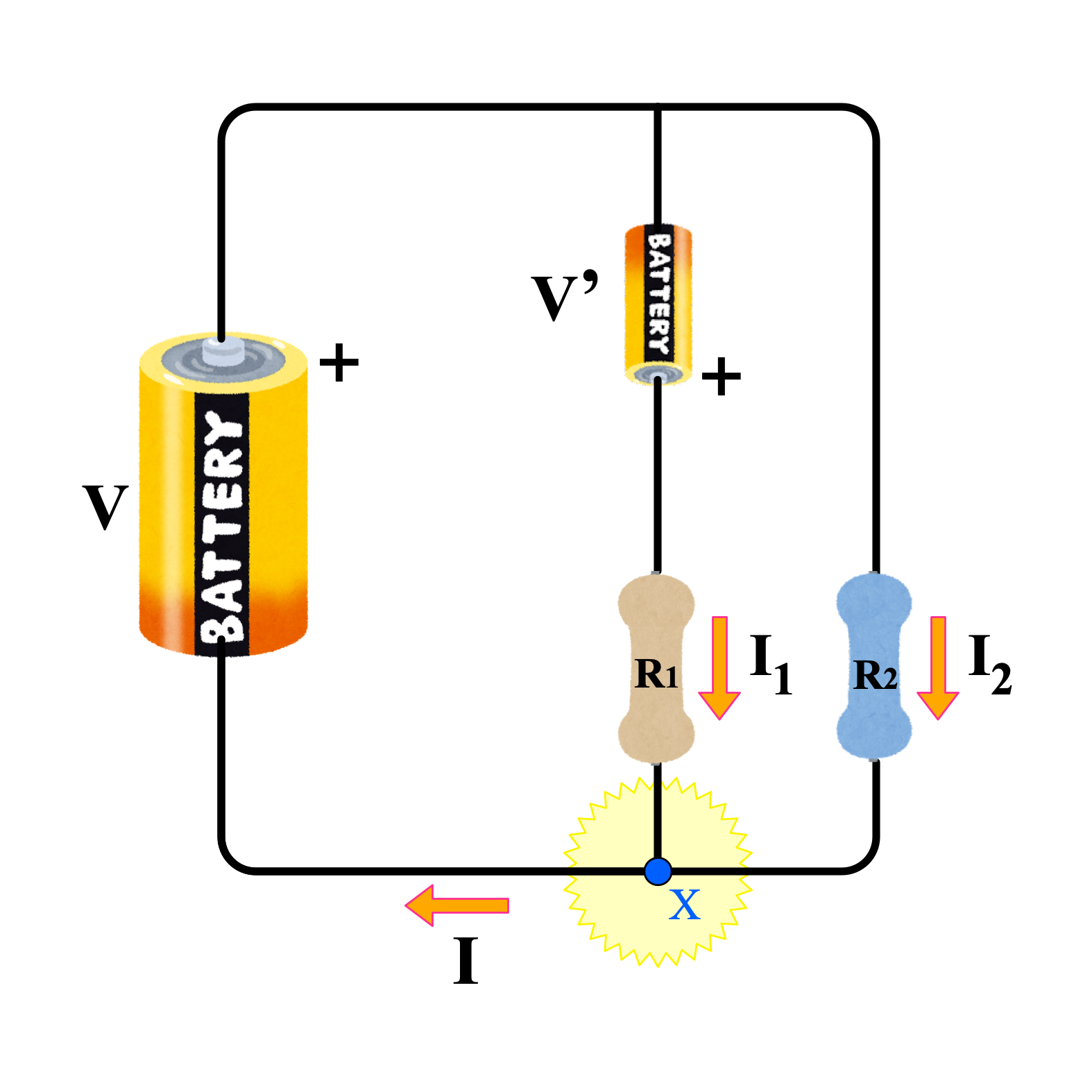
ユーリ「だって、ほら、この《X地点》で合流するはずだもん」
電流は《X地点》で合流する
僕「そうだね」
ユーリ「$I_1,I_2$ が《X地点》で合流して、 $I$ が出て行くんだから、 $I_1 + I_2 = I$ になる。そーでしょ?」
僕「うん。それはすごく大事! そして一般的にもいえる」
ユーリ「何が?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2021年9月17日)