![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
双倉図書館の一般講座《リンクとストラクチャー》でアルゴリズムを学んできたテトラちゃんは、 自分の理解のため、学んだことを僕に向けて《講義》している。
これまでに、 数列の中から最大の値を求めるMAX-VALUEを題材にして議論をしてきた(第321回参照)。
僕「テトラちゃんが教えてくれたから、ノードとリンクを使った線形リストについてはだいぶわかったと思うよ。ありがとう」
テトラ「い、いえ……あたしこそ、先輩に説明しながら理解が深まりました」
僕「気がついたことがあるんだけど……MAX-VALUEのアルゴリズムを《配列で実装した場合》と《線形リストで実装した場合》を比べてみると、うまく対応がついているよね」
テトラ「はいっ! そうですよねっ!」
僕「たとえば《数列のすべての要素を確かめたかどうか》という判定をしている部分は、 どっちもwhileの条件に書かれていて……」
List 5(再掲)(第321回参照)
MAX-VALUE: 最大値をもとめるアルゴリズム(配列版)
入力
出力
手続き
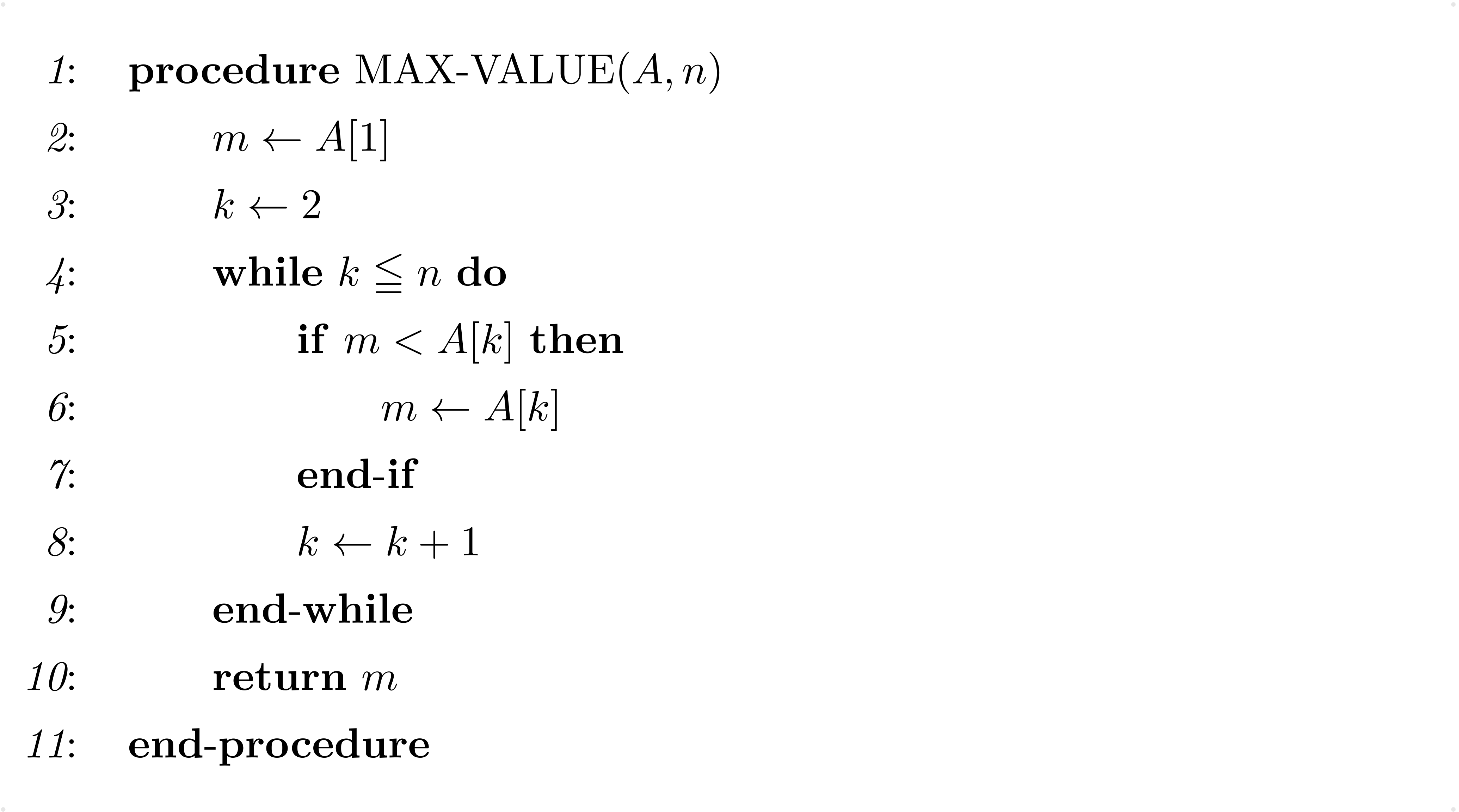
例: $L = \LLRR{31,41,59,26}, n = 4$ で、最初に4行目に来たときの様子

List 6(再掲)(第321回参照)
MAX-VALUE: 最大値をもとめるアルゴリズム(線形リスト版)
入力
出力
手続き

例: $L = \LLRR{31,41,59,26}$ で、最初に5行目に来たときの様子

テトラ「はい。《すべての要素を確かめた》という条件は、実装の仕方で変わりますが、ちゃんと対応がついています。 《配列で実装した場合》は、kという変数の値が要素数を越えたときです。 《線形リストで実装した場合》は、cという変数の値がnilになったときになりますね。 その他にもきれいに対応がついています。たとえば《kを1増やす》と《cにc.nextを代入する》のが対応しています。 これは《次の要素を調べるための準備》になりますね」

僕「うん。書き方は違うけれど、うまく対応してるなあと思ったんだ」
テトラ「このお話、 双倉図書館であたしが聞いた一般講座では《抽象度を変えて理解する》と教えていただきました」
僕「抽象度を変える?」
テトラ「はいはい。たとえば $k \LEQ n$ という式を見たときに《変数kの値は変数nの値以下である》と理解する抽象度と、《まだ調べていない要素がある》と理解する抽象度は違います」
僕「なるほど。《変数kの値は変数nの値以下である》という方が抽象度は……高いのかな、低いのかな」
テトラ「講義では《低い》としていましたね。 《実装寄り》という表現もありました。コンピュータという具体的なものに近いということでしょうか」
僕「コンピュータに近いの方が抽象度が低くて具体的なんだね」
テトラ「実装寄りの抽象度で理解しますと、次の二つの式はまったく違うように見えます」
僕「……」
テトラ「でもこの二つの式はどちらも、List 5とList 6というプログラムの中にそれぞれ置けば《数列を最後まで調べたかどうか》を表しているといえます。つまり、まったく違うように見えた二つの式も、抽象度を上げると同じ意味に見える。それが《抽象度を変えて理解する》ことなんです」
僕「なるほどなあ! 字面にとらわれず、抽象度を上げて理解することが大切なんだね!」
テトラ「そうなんです! あ、ええっと……そうなんですが、《抽象度を上げる》だけではなくて《抽象度を変える》ことが大事だそうです。必要に応じて抽象度を上げて理解し、必要に応じて抽象度を下げて理解する。必要とあらば、ぐぐっと実装寄りに理解することも大切……ということでした」
僕「……」
テトラ「せ、説明が下手ですみません」
僕「いやいや! 逆だよ。テトラちゃんの説明はすごくよくわかる。《抽象度を上げる》って表現、ミルカさんが言いそうだなって思っていたんだ。《抽象度を下げる》ことも大事なんだね」
テトラ「はい……ああ、それから《抽象度を変えて理解する》ことがどうして大事なのかという話題もありました」
テトラちゃんは用意してきたノートをめくりながらそう言った。
僕に《講義》するため、彼女はずいぶん準備をしてきたんだな。
僕「《抽象度を変えて理解する》ことがどうして大事か? うーん……改めて答えようとすると難しいな。 どうして大事なんだろう」
テトラ「はい。理由はいくつかありますが、たとえば《アルゴリズムの誤りを見つけやすくなるから》だそうです。なるほどですよね」
僕「なるほど……」
テトラ「アルゴリズムを複数の方法で実装したり、 プログラムを移植したりすると誤りが見つかりやすくなることも多いそうです。 《移植》ってすごい表現ですよね。 一つのプログラムを別の動作環境で動かすために書き直したり、修正したりすることだそうです」
僕「検算と似ている発想かもしれない。数学の問題で答えが出たあと、答えを吟味するのにも似てるかな」
テトラ「ああ、そうですね。描いた絵を左右反転しておかしな点を見つけるのにも似ています」
僕「ところでテトラちゃん……テトラ先生、質問です!」
僕はいつものテトラちゃんを真似して、さっと手を挙げた。
テトラ「はい、何でしょう」
テトラちゃんはそんな僕をにこにこしながら指さした。
僕「さっきから気になってたんだけど、配列で実装する方が単純なように思うんだ。どうして線形リストなんて使うんだろう」
テトラ「とてもいい質問ですっ! たとえば、配列の途中にある数を《先頭に移動》したいとします。 すると、それまで1番目にあった数は2番目に、2番目にあった数は3番目に……のようにずるずると移動しなくてはいけません。 こんなふうになります」
配列の途中にある要素を先頭に移動する
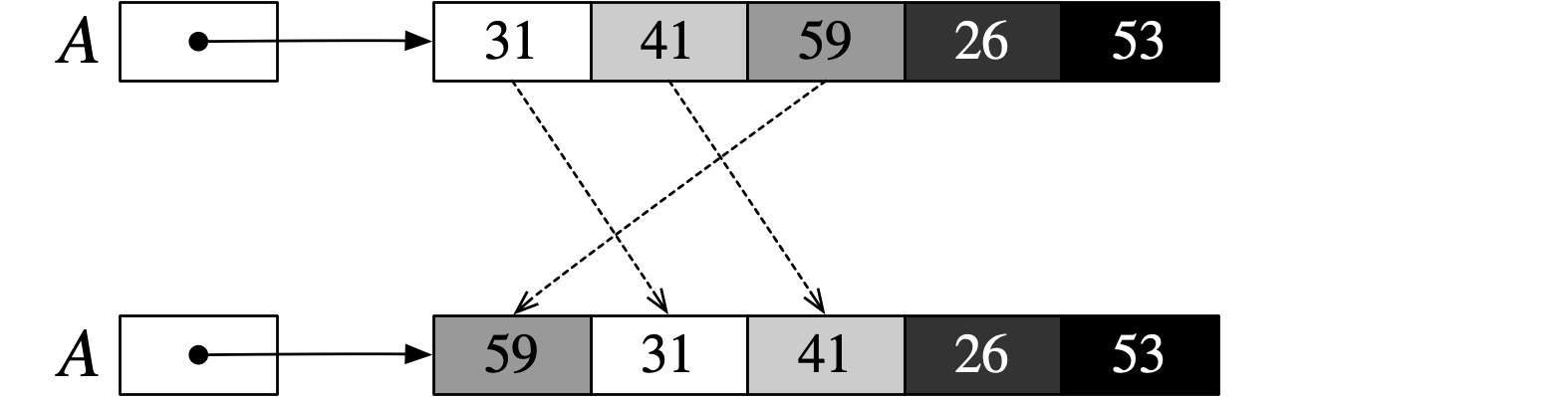
僕「ああ、確かにそうだね。単に、 $$ A[1] \leftarrow A[k] $$ のように代入しちゃだめか。 $A[1]$ の情報が消えちゃうから?」
テトラ「そうですっ! 配列の各要素は、コンピュータ上ではメモリ上で連続した領域に置かれているので、途中に要素を挿入したり、途中から要素を削除したりすると、大量の移動が発生してしまうんです……」
僕「なるほど。たとえば配列で最後の要素を先頭に持ってくるとなると、残り全部を一つ後ろに移さないといけないんだね」
配列の最後にある要素を先頭に移動する

テトラ「そうです。この例では5個しかありませんが、 データの個数に合わせて掛かる時間が増えてしまいます」
僕「線形リストだと、リンクが指すノードを切り換えるだけで済むということ……」
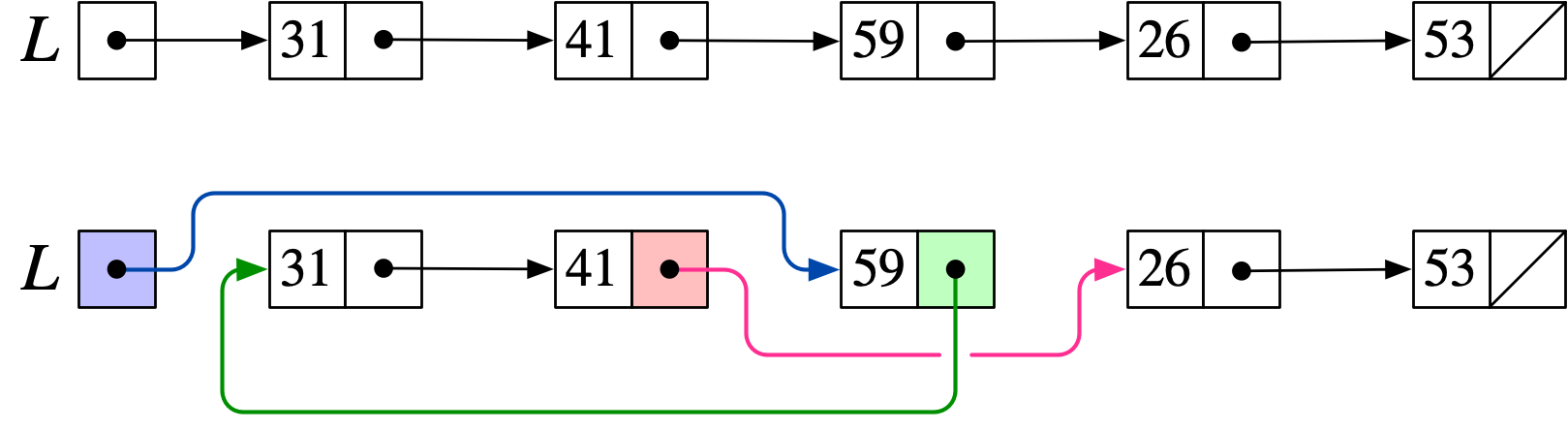
テトラ「そうです。こちらをご覧ください。先頭に持ってくる要素が途中にある場合でも、最後にある場合でも書き換えるnextフィールドの個数は変わりませんっ!」
線形リストの途中にある要素を先頭に移動する
線形リストの最後にある要素を先頭に移動する
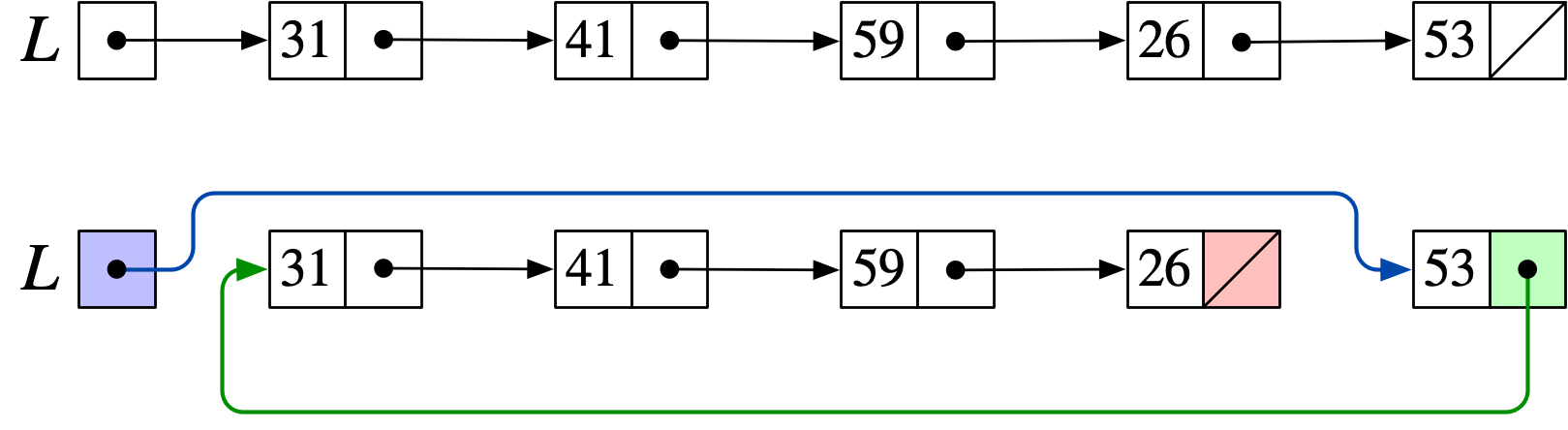
僕「なるほどねえ……だとすると確かに線形リストを考える価値はありそうだね。 でもそうなると順番が大事になりそう」
テトラ「順番といいますと?」
僕「リンクを切り換える順番だよ。 ほら、プログラムでは、数学と違って変数の値が書き換えられるよね。 だから、リンクを切り換える順番を間違えると期待したようなリンクにならないんじゃないかと思ったんだ」
テトラ「まさに、その通りですっ! あたし、演習でたくさん間違えましたよ……」
テトラちゃんはそう言いながら両手で頭を抱えた。
僕「へえ、演習の時間もあったんだ」
テトラ「はい。ところどころで小さなプログラムを書きながら進みましたので、まさに《例示は理解の試金石》でした。 お話を聞いたり、書かれたプログラムを読んだりしているときは理解したつもりになっていても、 実際に書こうとすると、自分がまったく理解していなかったということがありありとわかるんです。それはもう驚くほどです」
僕「そうなんだ……」
テトラ「先輩も、やってみます?」
テトラちゃんの大きな目がきらりと光った。この輝きはめずらしいぞ。
僕「う、うん……やってみたいな」
テトラ「では問題1です! 線形リストが状態Aで、Lとpが与えられているとします。これを状態Bに変えるプログラムを書いてください!」
問題1 状態Aを状態Bに変えるプログラムを書きましょう(pが指しているノードを先頭に移動)
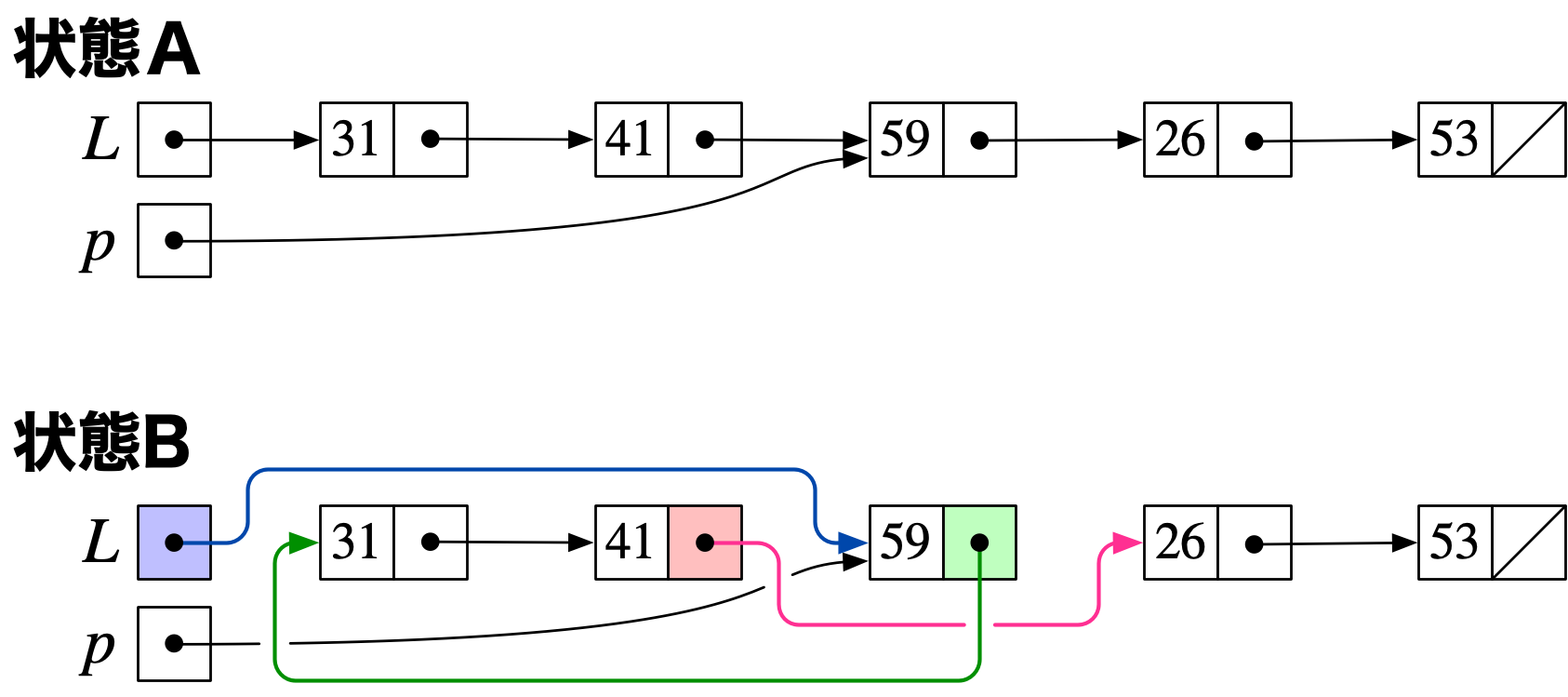
僕は考える。
順番が大事になるのは確かだけど……とはいえ、リンクを切り換えるだけなんだから、 何回か代入するだけでいいはず。
代入は何回必要だろうか……
うん、書き換えるnextフィールドは3箇所あるから、3回だけ代入すれば……いや? どうなる?

無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2021年5月7日)