![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
双倉図書館の一般講座《リンクとストラクチャー》でアルゴリズムを学んできたテトラちゃんは、 自分の理解のため、学んだことを僕に向けて《講義》している。
最大の値を求めるMAX-VALUEを題材にしたり(第321回参照)、 線形リストのノードを先頭に移動するMOVE-TO-FIRSTを題材にしたり(第322回参照)と、 いろんな議論を重ねてきた。
いまは、 リストヘッド付き線形リストというデータ構造を議論しているところ。
テトラ「リストヘッドがあると、List 9のようにシンプルに書けるんですよ!」
List 9:リストヘッド付き線形リスト版MOVE-TO-FIRST

実行例
僕はしばらくList 9を眺めた。
うん、確かにずいぶんシンプルになったけど……!
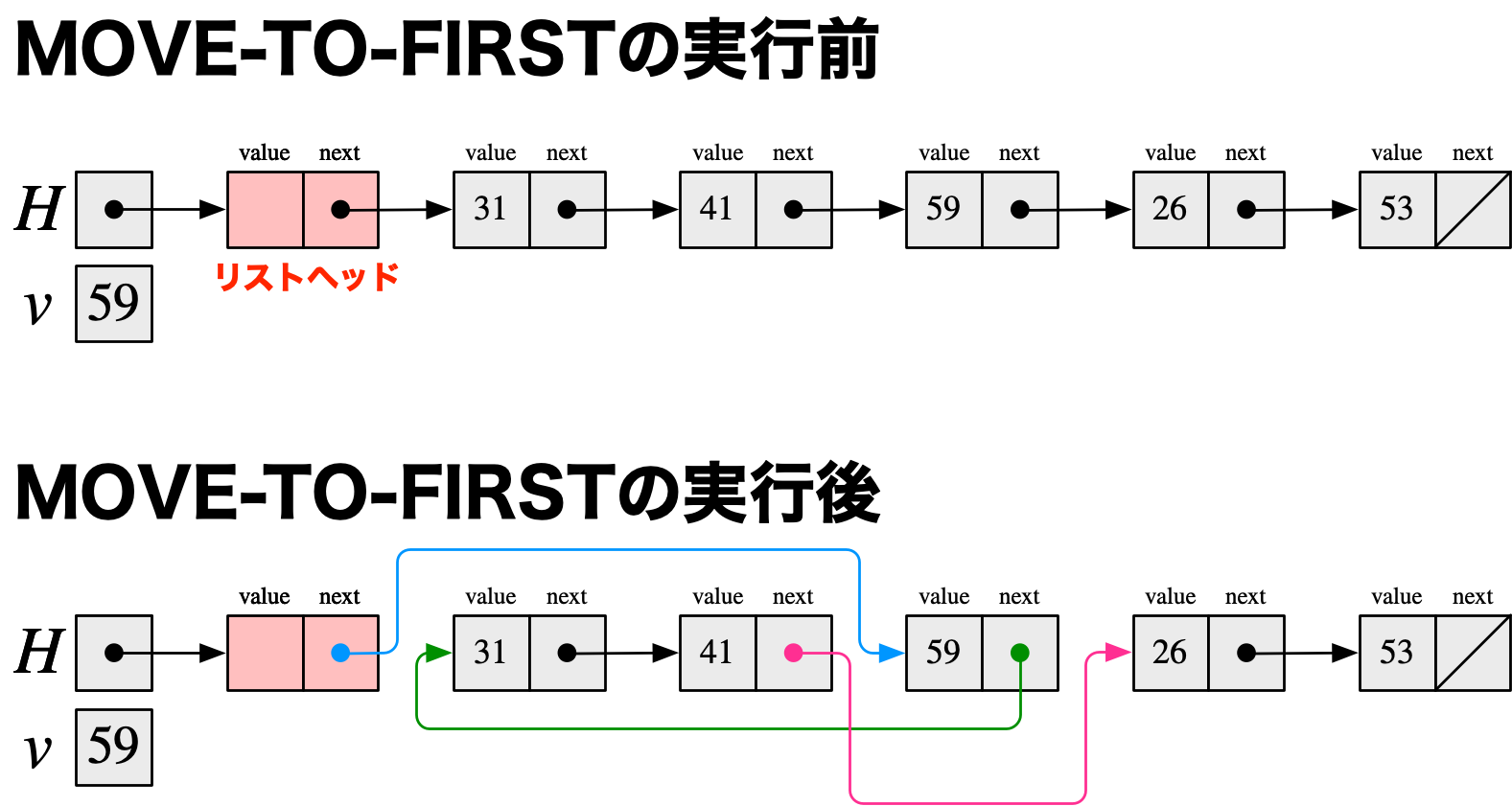
僕「ちょっと待って。これって $a_1 = v$ のときでもうまくいく? 怪しくない? だって、 H5〜H9ではどんなときでもリンクを切り換えてしまうよね?」
テトラ「驚くことに、うまく行くんですよ!」
テトラちゃんが図を描こうとしているあいだ、僕はもう一度List 9を読み返した。
僕「いやいや、駄目だよ。だって、 $a_1 = v$ のときは、pはリストヘッドを指していて、qは最初のノードを指している。 その状態でH6にやってくる。H6はいいとして、H7がまずいよ。だって、 $$ q.\Fnext \leftarrow H.\Fnext $$ を実行してしまったら、最初のノードは自分自身を指してしまうことになる! 線形リストが途中で切れてしまうはずだよ」
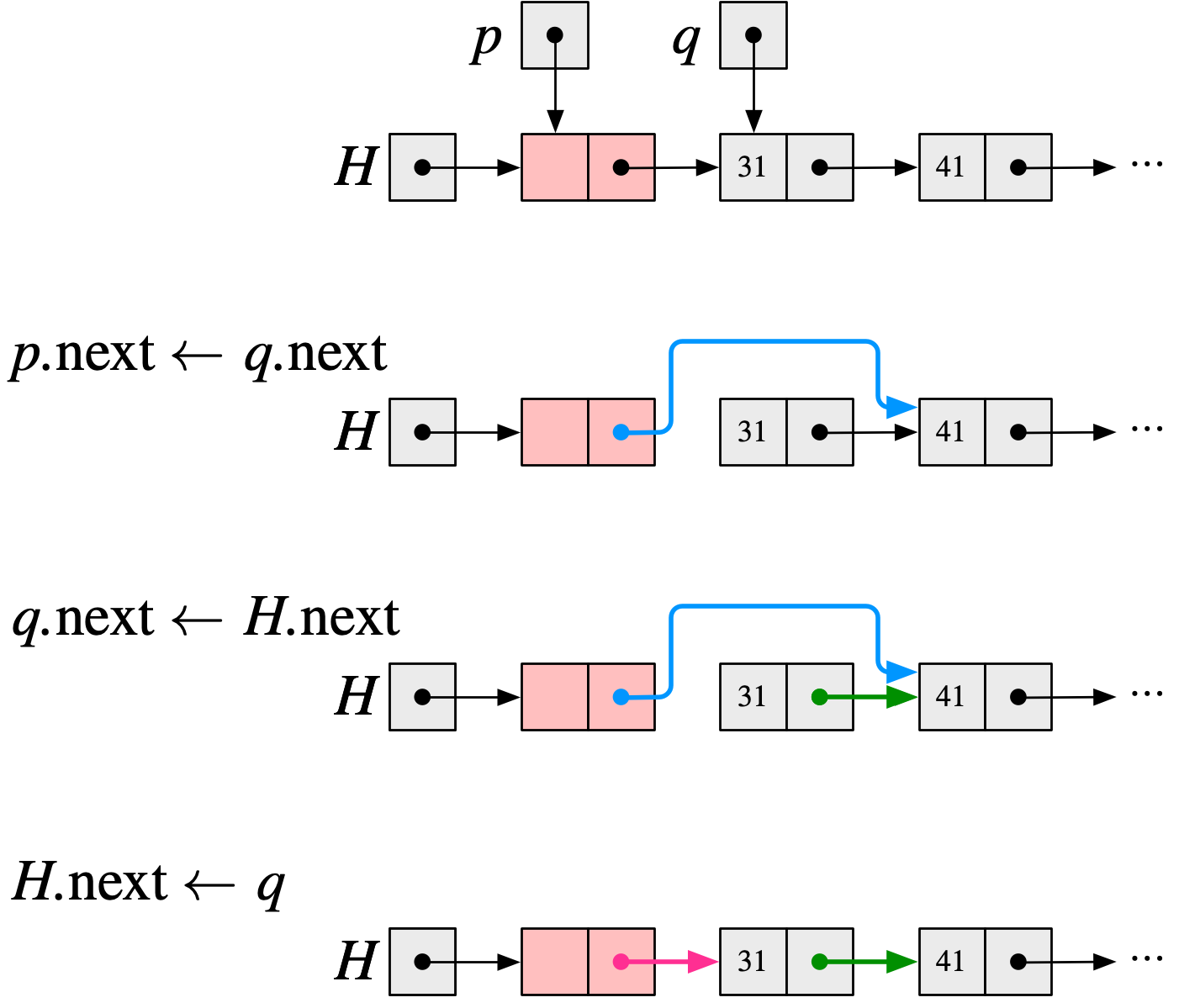
テトラ「……ところがそうはならないんですよ、先輩。 こちらのステップ・バイ・ステップで描いた図をごらんください。 先輩が気になさっていたH7を実行するときには、 $H.\Fnext$ の値は最初のノードではなくなっているので、 途中で切れることはないんですっ!」
HEAD-TO-FIRST(H, v)でvに31が渡された場合の、H6, H7, H8の動き
僕は、彼女が描いた図を見てショックを受けた。
僕「本当だね。うーん……」
テトラ「もちろんこの場合、代入を三回行って結局は何も変わっていないことになります。 でも、先頭を特別扱いしなくて済むとプログラムはシンプルになりますので、 間違いが入り込む危険性も少なくなります。 リストヘッド付きの線形リストでは、そういうことがよくあるそうです」
僕「いや……それはわかったんだけど」
テトラ「先輩?」
僕「テトラちゃんはきちんと図を描いて説明してくれたけれど、 僕は先を急いで読もうとしてしまい……まちがった。 たった三ステップしかないんだから、ほんの少しの時間を使うだけですぐに図を描けるし、 図を描きさえすれば自分のまちがいに気がつく。 その《ほんの少しの時間》を、自分が無意識のうちに惜しんだことがショックなんだ」
テトラ「双倉図書館の一般講座でも、講師の先生はそんなことをおっしゃっていました。 《ステップ・バイ・ステップ》で確かめることが、結局のところ近道になることが多いというお話です。 あたし、それにすごく励まされました。 たとえ、すごいひらめきがやってこなくても、 根気よく確かめることはあたしにもできそうだからです!」
僕「なるほどねえ……」
そしてまた僕は『グラフを描かないのが君の弱点だ』といったミルカさんのことを思い出した。
グラフに限った話じゃないなあ……
テトラ「先輩はすっと理解してしまいましたが、あたしはアルゴリズムの一般講座で悩んだのは、たとえば、 $$ p \leftarrow H $$ という代入でした。この表記が……」
僕「これはHをpに代入するということだよね」
テトラ「はい。もちろんそうなんですが、あたしが引っかかったのは、 $$ p \leftarrow H $$ と表現されたとき、pとHとでは意味が違うという点でした」
僕「意味が違う?」
テトラ「はい。こういうことです」
僕「……ああ、確かにそうだね。 $p \leftarrow H$ と書かれているときに行われるのは、こうだから」
テトラ「はいはい! そういうことです。図を描いていて、それに気付いてからプログラムが読みやすくなりました。 講師の先生にお尋ねしたところ、左辺値(さへんち)と右辺値(うへんち)という名前がついているそうです。 《左辺値》は《値を保持している場所を表す値》のことで《メモリのアドレス》と思えばわかりやすいです」
僕「《左辺値》は代入の左辺に来ることができる値ってことだね。代入できる場所を表す値だ」
テトラ「だいたいはそうなんですが、プログラミング言語によってはメモリのアドレスは表しているけれど、 代入できない定数のような概念があるので《左辺値》のことを《代入できる場所を表す値》というのは不正確だそうです」
僕「そうなんだね……ところで《右辺値》の方は123のような値のことかな」
テトラ「はい。《右辺値》は、123のような値の場合もあるし、《左辺値》を《右辺値》として扱う場合もあるそうです。 先ほどの $p \leftarrow H$ の場合もそうですよね」
僕「変数Hの値は、ノードを表すアドレスだから《左辺値》といえるけど、 $$ p \leftarrow H $$ では、その値を変数pに代入する《右辺値》として扱っている?」
テトラ「そうです、そうです。いずれにしても、図を描けばあまりまちがうことはありません」
僕「いわれてみると、 $$ p.\Fnext \leftarrow q.\Fnext $$ は自然に読んじゃったけど、左辺と右辺で確かに違うものを表しているね」
$p.\Fnext \leftarrow q.\Fnext$
左辺の $p.\Fnext$ は、《pが指している先にあるノードの、nextフィールドという場所》を表している。
右辺の $q.\Fnext$ は、《qが指している先にあるノードの、nextフィールドに保持されている値》を表している。
テトラ「そうです! この場合、代入によって、同じ場所を指すようになるわけですね。図に描くとわかりやすいです」
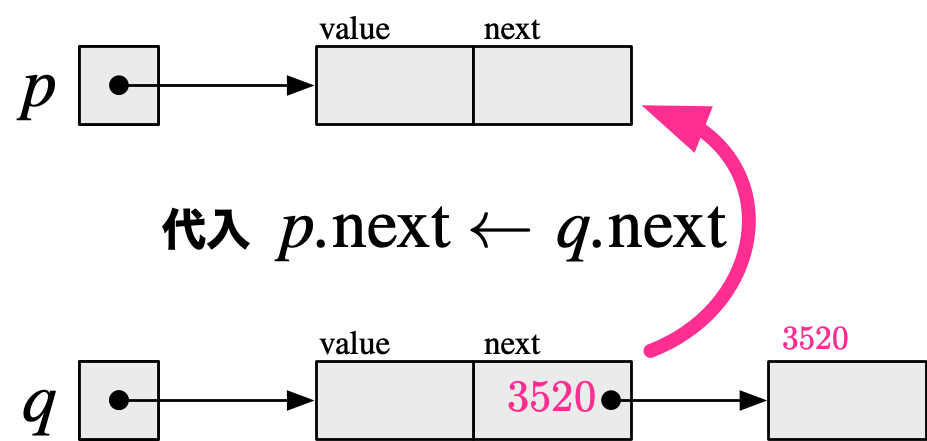
※nextフィールドに書かれた数値はアドレスの例を表しているものとします。

※nextフィールドに書かれた数値はアドレスの例を表しているものとします。
テトラ「それではここで先輩にクイズをひとつ、お出しします!」
テトラちゃんはにこやかにそう言って、人差し指を立てた。
僕「おっ?」
テトラ「線形リストにリストヘッドをつけて、プログラムがシンプルになった理由は何でしょう?」
僕「理由……?」

テトラ「いかがですか?」
僕「リストヘッドをつけると、先頭を特別扱いしなくて良くなるから、かな。 List 8のテトラちゃんのプログラムがまさに先頭を特別扱いしていたから(第322回参照)」
テトラ「はい、そうですね。先頭を特別扱いしなくてよくなります。 もう少しいいますと、こうなります」
リストヘッドがない場合
リストヘッドがある場合
僕「確かにそうなるね。リストヘッドという特別のノードを最初に置くことで、 すべてのノードを統一的に扱えるようになる。だからプログラムがシンプルになる」
テトラ「はい。いうなれば《一様性》や《均一性》があるためにシンプルになるんです」
僕「なるほどね」
テトラ「ところで先輩に、もうひとつ、クイズをお出しします」
僕「今度は何だろう」
テトラ「あたしたちは《リストヘッド付き線形リスト》を扱ってきましたけれど、 ここにはまだ《一様性》に欠けている部分があります。 それはどこでしょうか?」
僕「うーん……」

テトラ「いかがでしょう?」
僕「たぶん、リストの最後だね。リストの最後にあるノードには《一つ次のノード》が存在しない。 最後のノードのnextフィールドには、nilが保持されている。 でも、nextフィールドにnilが保持されているのは最後のノードだけ。ここじゃない?」
テトラ「はいっ! 正解です!」
僕「ということは、《リストテール付きの線形リスト》を考えることができるんだね」
テトラ「それでもいいんですが……もっと便利なものがあります。それは《リストヘッド付き循環リスト》です」
僕「循環リスト?」
テトラ「はい。この図のように、リスト最後のノードのnextフィールドが必ずリストヘッドを指すようにするんです。 そうすると、山手線のようにぐるっと回るデータ構造ができあがります。 これが《リストヘッド付き循環リスト》です。nextフィールドにnilはもう出てこなくなります」
リストヘッド付き循環リスト

僕「ちょっと待って。だったら、どうやってリストの終わりを判定するんだろう……ああ、 リストヘッドかどうかで判定すればいいのか」
テトラ「その通りです! 《リストヘッドを指している》という状況を《nilである》という扱いにするんです」
僕「……」
テトラ「な、何かおかしいでしょうか?」
僕「いや、おかしくはないし、確かに《一様性》はわかるんだけど、それだけでそんなにシンプルになるのかなあ……」
テトラ「では問題3ですっ! プログラムを書きましょうっ!」
問題3(数列内に値が存在するかどうかの判定)
与えられたリストヘッド付き循環リストCに含まれているノードのうち、 valueフィールドの値が、与えられたvに等しいものがあるかどうかを判定する手続きCONTAINS(C, v)を書いてください。
手続き
入力
出力
CONTAINS(C,v)への入力&出力例1
入力
出力
CONTAINS(C,v)への入力&出力例2
入力
出力
僕「ああ、これは簡単だね……っとっと。いや、ちゃんと考えないと」

テトラ「……いかがでしょうか?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2021年5月14日)