![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
ミルカさん:数学が好きな高校生。 僕のクラスメート。長い黒髪の《饒舌才媛》。
僕たちは、こんな問題を考えていた。
問題
鋭角三角形の三個の角をそれぞれ $A,B,C$ とすると、 $$ \tan A + \tan B + \tan C = \tan A \tan B \tan C $$ が成り立つことを証明せよ。
僕は $\tan(\pi - C) = -\tan C$ を使って《まっすぐな証明》を終えた(第317回参照)。
ミルカ「こんな《広がる証明》もある。つまり複素平面を使う」
テトラ「この問題に、複素数が出てくる……?」

ミルカ「さっき、 $\tan$ の加法定理を複素平面を使って考えた(第317回参照)。それと同じように考える」
テトラ「複素数で《積の偏角は、偏角の和》になる、それをまた使うんですか?」
僕「僕もそれはちらっと思ったよ。ただ……加法定理では $\tan(\alpha + \beta)$ の中に和が出てきたけれど、この問題の式、 $$ \tan A + \tan B + \tan C = \tan A \tan B \tan C $$ には角度の和は出てきていないからなあ」
テトラ「$\tan A + \tan B + \tan C$ は $\tan(A + B + C)$ とは違いますよね……」
僕「違うね。それに $A + B + C = \pi$ なんだから、 $$ \tan (A + B + C) = \tan \pi = 0 $$ だよ。関係式というよりも値が出てきてしまう」
テトラ「ああ、タンジェントの値が決まってしまうんですね」
ミルカ「それが、のちのち効いてくる」
テトラ「はい?」
ミルカ「ともかく、三個の複素数 $z_1,z_2,z_3$ を次のように定めよう」
$$ \begin{align*} z_1 &= 1 + i\tan A \\ z_2 &= 1 + i\tan B \\ z_3 &= 1 + i\tan C \end{align*} $$僕「これは加法定理のときと同じだね。二個じゃなくて三個になったけど。偏角がそれぞれ $A,B,C$ になっている複素数」
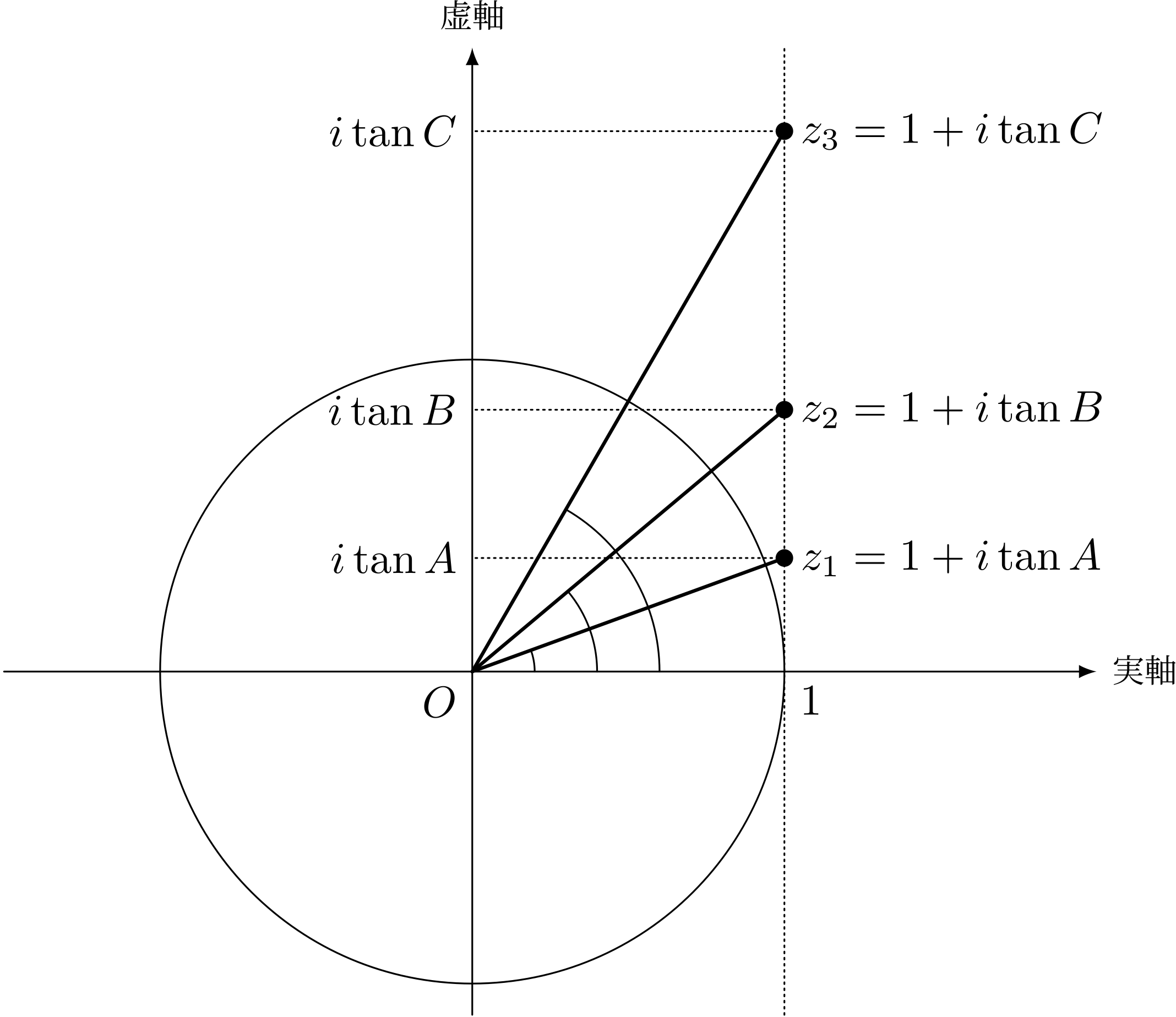
テトラ「そうですね。また積を取るんですか」
ミルカ「そうだ。そして何が出てくるかを観察する」
$$ \begin{align*} z_1z_2z_3 &= (1 + i\tan A)(1 + i\tan B)(1 + i\tan C) \\ &= \bigl((1 - \tan A\tan B) + i(\tan A + \tan B)\bigr)(1 + i\tan C) \\ \end{align*} $$僕「ああ、そうか。 $(1 + i\tan A)(1 + i\tan B)$ はさっき計算したからすぐにわかるんだね(第317回参照)」
テトラ「《いち引くタンタン、タン足すタン》ですね」
$$ (1 + i\tan A)(1 + i\tan B) = (\underbrace{1 - \tan A \tan B}_{\REMTEXT{いち引くタンタン}}) + i (\underbrace{\tan A + \tan B}_{\REMTEXT{タン足すタン}}) $$ミルカ「計算を続ける。ただの展開だ」
$$ \begin{align*} z_1z_2z_3 &= \cdots \\ &= \bigl((1 - \tan A\tan B) + i(\tan A + \tan B)\bigr)(1 + i\tan C) \\ &= (1 - \tan A\tan B) + i(\tan A + \tan B) \\ & \qquad + i\bigl((1 - \tan A\tan B) + i(\tan A + \tan B)\bigr)\tan C \\ &= (1 - \tan A\tan B) + i(\tan A + \tan B) \\ & \qquad + i(1 - \tan A\tan B)\tan C - (\tan A + \tan B)\tan C \\ &= (1 - \tan A\tan B) + i(\tan A + \tan B) \\ & \qquad + i\tan C - i\tan A\tan B\tan C - \tan A\tan C - \tan B\tan C \\ &= 1 - \tan A\tan B + i\tan A + i\tan B \\ & \qquad + i\tan C - i\tan A\tan B\tan C - \tan A\tan C - \tan B\tan C \\ &= (1 - \tan A\tan B - \tan A\tan C - \tan B\tan C) \\ & \qquad + i(\tan A + \tan B + \tan C - \tan A\tan B\tan C) \\ \end{align*} $$僕「なるほど! これはおもしろいな!」
テトラ「これが……?」
$$ \begin{align*} z_1z_2z_3 &= (1 - \tan A\tan B - \tan A\tan C - \tan B\tan C) \\ & \qquad + i(\tan A + \tan B + \tan C - \tan A\tan B\tan C) \\ \end{align*} $$ミルカ「私たちがやったことはこれだ」
僕「ゴール直前だね」
ミルカ「そう。ここから私たちが求める式の証明までは、ほんの一歩だ」
テトラ「あ、あたしにとっても?」
ミルカ「恐らくは」
テトラ「先輩方っ! ここからはヒント無用です。テトラ、考えます……」
問題
鋭角三角形の三個の角をそれぞれ $A,B,C$ とすると、 $$ \tan A + \tan B + \tan C = \tan A \tan B \tan C $$ が成り立つことを証明せよ。
いま、わかっていること
$$ \begin{align*} & (1 + i\tan A)(1 + i\tan B)(1 + i\tan C) \\ &\qquad = (1 - \tan A\tan B - \tan A\tan C - \tan B\tan C) \\ & \qquad\qquad + i(\tan A + \tan B + \tan C - \tan A\tan B\tan C) \end{align*} $$

ミルカ「……」
僕「……」
テトラ「……た、たぶんわかりました」
僕「どうぞ、どうぞ」
テトラ「$\tan$ の加法定理のときと同じに考えます。つまり、 $$ z_1z_2z_3 = a + ib $$ という複素数になったとします。 $a,b$ は実数です」
僕「うん」
テトラ「そうして、 $z_1z_2z_3$ の偏角を……たとえば $\theta$ としますと、 $$ \tan\theta = \frac{b}{a} $$ になります」
$z_1z_2z_3 = a + ib$ になったとすると……
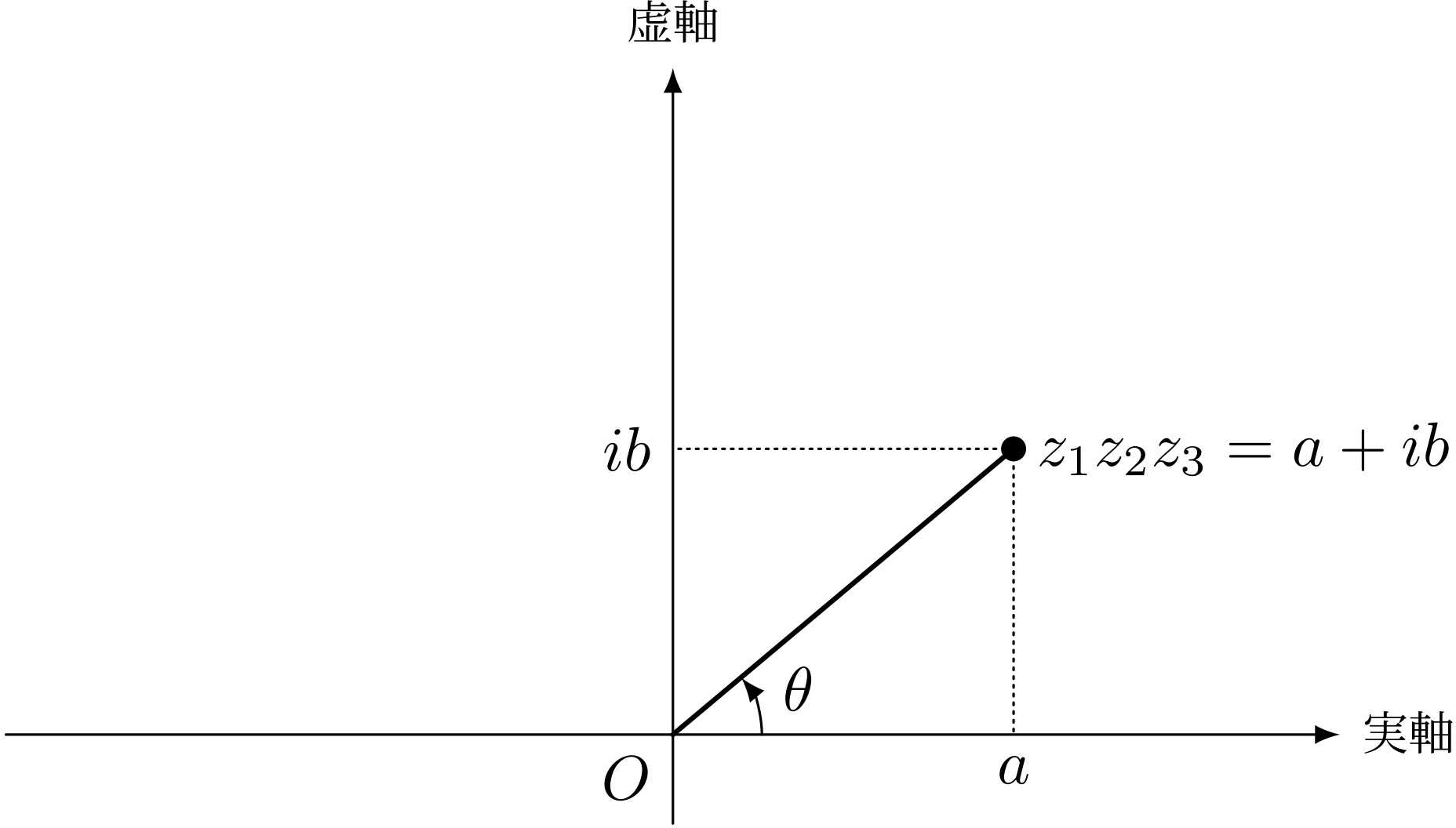
$$ \tan\theta = \frac b a $$
僕「$a = 0$ にならなければ、そうだね」
テトラ「え、ええと……たぶん $a \neq 0$ だと思うんですが……」
ミルカ「まずはテトラの話を聞こう」
僕「あ、そうだね。ごめん」
テトラ「いったん $a \neq 0$ として話を進めます……」
$\theta$ を積の偏角としましたが、実は、 $$ \theta = \pi $$ となることがすぐにわかります。なぜなら、 $z_1z_2z_3$ の偏角の和だからです。
$z_1,z_2,z_3$ の偏角はそれぞれ $A,B,C$ です。
複素数では《積の偏角は、偏角の和》ですから、 複素数 $z_1z_2z_3$ の偏角は、 $\theta = A + B + C$ となります。
ところで、三角形の内角の和は $\pi$ なので、 $$ \theta = \pi $$ といえます。
偏角が $\pi$ ということはですね、複素数はこう……ぐるっと回って実軸にペタンと着地します。
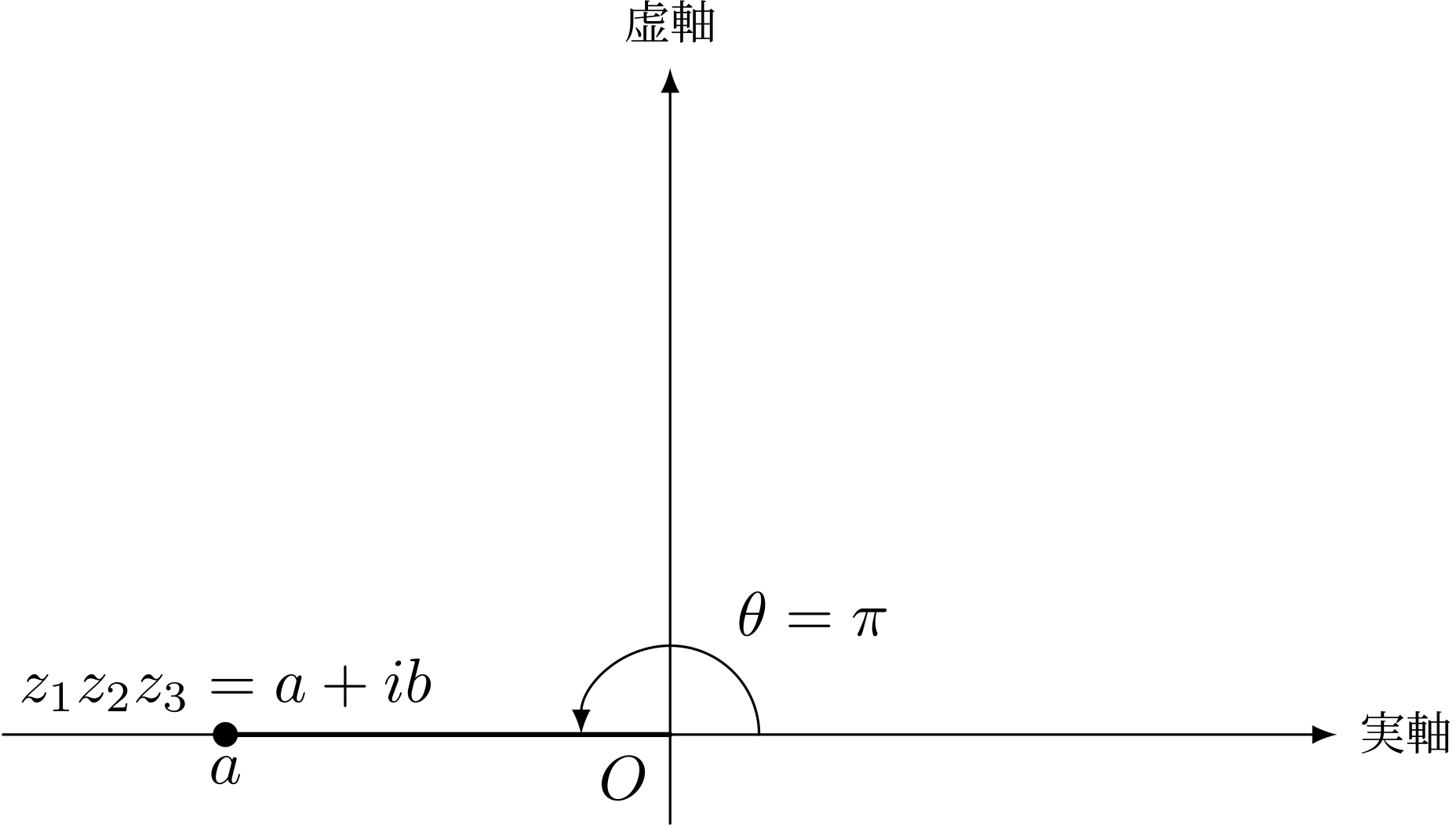
いいかえると、この複素数 $z_1z_2z_3$ の虚部はゼロなんです!
つまり、 $$ z_1z_2z_3 = a + ib $$ と置いたならば $b = 0$ ということです。
先ほどミルカさんの計算から、、 $$ \begin{align*} z_1z_2z_3 &= \underbrace{(1 - \tan A\tan B - \tan A\tan C - \tan B\tan C)}_{=a} \\ & \qquad + i\underbrace{(\tan A + \tan B + \tan C - \tan A\tan B\tan C)}_{=b} \\ \end{align*} $$ になっていて、 $b = 0$ ですから…… $$ \tan A + \tan B + \tan C - \tan A\tan B\tan C = 0 $$ すなわち、 $$ \tan A + \tan B + \tan C = \tan A\tan B\tan C $$ が言えました!
(証明終わり)ですっ!
ミルカ「とてもおもしろい」
僕「複素平面を利用した《広がる証明》だね!」
テトラ「おもしろいですねえ……ペタンと着地! あっ、それから確かに $a \neq 0$ です。なぜなら、もしも $a = 0$ だとしたら、 $a = b = 0$ ということで $z_1z_2z_3 = 0$ になってしまいますから」
僕「そうだね。 $z_1 \neq 0, z_2 \neq 0, z_3 \neq 0$ だから積は $0$ にならない」
ミルカ「この証明は、一つのものを《二つの視点》で見ているところがおもしろい」
テトラ「《二つの視点》……といいますと?」
僕「複素数を《実部と虚部》で見る視点と《絶対値と偏角》で見る視点だよね?」
ミルカ「そう」
僕「$z_1z_2z_3$ を展開するときでは最終的に、 $$ z_1z_2z_3 = a + ib $$ のように $a,b$ という《実部と虚部》に分けたことになる。成分を計算したんだね」
テトラ「そうですね」
僕「複素数の偏角を考えるときというのは、 $$ z_1z_2z_3 = r(\cos\theta + i\sin\theta) $$ のように、 $r,\theta$ という《絶対値と偏角》に分けたことになるよね。 $r$ は絶対値、 $\theta$ は偏角。極形式だ」
テトラ「ああ、そうですね! そうなりますね! 確かに複素数を《二つの視点》から見ています。……で、でも、どうしてそれで証明ができたのでしょう。あっ、待ってください。これは《結果を一目でとらえられるか》ですね」
僕「うん、そうだね。《二つの視点》から見たときの鍵はどこにあったんだろう」
テトラ「結局、一つのものを《二つの視点》で見るというのは、この等式が成り立つときです」
$$ a + ib = r(\cos\theta + i\sin\theta) $$僕「うんうん。積を計算したときに、 $$ b = \tan A + \tan B + \tan C - \tan A\tan B\tan C $$ という僕たちが証明したい式の形が出てきた。僕たちが示したいのは $b = 0$ だけど……」
ミルカ「しかし、どうしたら $b = 0$ が示せるのか、すぐにはわからない」
テトラ「《三角形の内角の和》という条件を使えば、 $\theta = A + B + C$ から $b = 0$ が示せる! ペタンと着地ですっ!」
ミルカ「それは、 $$ \sin\theta = \sin(A + B + C) = \sin\pi = 0 $$ といってるわけだ」
僕「そうだね。計算すれば《実部と虚部》の視点で見ることができて、 《絶対値と偏角》の視点で見ることによってそのうちの虚部の値が求められた。 それが僕たちの示したかったこと!」
※複素平面を使ったこの証明は、栗田哲也『難関大入試数学・発展していく三角関数』(東京出版)を参考にしています。
テトラ「《三角関数》の計算練習をしていたと思ったら、いつのまにか《複素数》のお話になっていました。楽しいですね!」
ミルカ「それなら今度は《積分》の話をしよう」
問題
$$ \int_{0}^{1} \frac{1}{1 + x^2} dx = \REMTEXT{?} $$
僕「なるほど、確かに三角関数はここにも出てくるね」
テトラ「えっ、何がですか? そんなに一瞬でわかるものなんですか? あたしには、さっぱり……」
僕「いやいや、これは有名な問題だから、積分をならうときの例題で出てくるんだよ。だから、一瞬でわからなくても大丈夫。何回か練習していると、自然に覚えちゃう」
テトラ「へえ……」
ミルカ「テトラは定積分はわかっている?」
テトラ「か、簡単なものなら……たとえば、これによく似た積分でこれならわかります」
$$ \int_1^2 \frac{1}{x^2} dx = \REMTEXT{?} $$ミルカ「ふむ」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 430本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2021年2月26日)