![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
ミルカさん:数学が好きな高校生。 僕のクラスメート。長い黒髪の《饒舌才媛》。
テトラ「$\tan$ を使って映画のスクリーンを《見込む角》を調べる問題はとてもおもしろかったです(第316回参照)」
僕「そうだね。いろんな解法がある問題はとても楽しい」
テトラ「ミルカさんの円周角を使った解法もすごかったんですが、あの問題がテストに出たとしたら制限時間中に思いつきそうな気はまったくしません……」
ミルカ「テトラが解いていた微分は堅実な方法だな」
テトラ「何だかそれって不思議ですよね」
僕「何が?」
テトラ「ミルカさんは図形で、先輩は相加相乗平均の関係で解いて、あたしは……先輩に助けていただきながら……微分を使って解きました。難しい方法だと確実に解けて、易しい方法だと解けるかどうかわからないというのが不思議です」
僕「《解けるかどうか》がわからないというより、《気付くかどうか》がわからないという感じだね。気付いてしまえば易しいかもしれないけれど、気付くところまで含めたら易しいとは言いにくいかなあ」
ミルカ「関数の最大値を求める際に微分を使う。それ自体には《ひらめき》は要らない。先人たちのおかげだ」
僕「《ひらめき》が要らないとまでは言いにくいけど、まずは試してみる定番の方法だよね」
テトラ「まずは試してみる定番の方法ですか……変な話かもしれませんが、最初から微分を学ばないのはどうしてでしょうか」
僕「微分を学ばないって、どういう意味?」
テトラ「あっ、つまり、学校で学ぶ順番としては、図形→相加相乗平均の関係→微分になるわけですよね」
僕「まあ、そうだね」
テトラ「もしも微分が、確実に解ける堅実で定番の方法なら……この問題に限らず最大値の問題を解くための強力な《武器》だとするなら……最初から微分を学べばいいと思ってしまったんです」
僕「しょっぱなから微分を学ぶってこと? それはずいぶん過激だね」
テトラ「そ、そうでしょうか」
僕「微分は大事だけど、そこに至るまでも数学のいろんな概念に触れていくのは大事なんじゃないのかな。角のイメージを持たなかったり、不等式の概念や式の扱いや関数がよくわからないうちに、さらにその関数を操作する微分について学ぶなんて、なかなかつらいし、かなり無茶だと思うんだけど」
テトラ「それは……確かにそうですね」
僕「便利な方法をいったん学んでしまうと『なーんだ、最初からこれを学べばいーじゃん!』となってしまうけど、それは順序立てて学んだ後からの視点かもしれないよ」
ミルカ「ユーリが憑依したな」
僕「山頂に行くならヘリコプター使えばいい、坂道を上らなくてもいい、というのはそうかもしれないけど、何だか違う気もするよね。無理に苦行をする必要はないけど」
テトラ「なるほど……」
ミルカ「そもそも私たちは最初から微分を学んでいるとはいえるな」
僕「え?」
ミルカ「私たちはまだ数学を学び始めたばかりだ。それなのにすでに微分のことを知っているし、計算もできる。《最初から微分を学んでいる》といえるのではないかな? さらにいうなら、人類が微分という道具を手に入れて整備するようになってから、まだ数百年しか経っていない。たったの数百年なのだ。私たちは微分が存在する時代に生きている」
ミルカさんの言葉に、僕たちはしばらく物思いにふけった。
テトラ「最近あたしは三角関数の練習をしているんですが、加法定理にもだいぶ慣れました。《しっかり覚える加法定理》も教えていただきましたし(第315回参照)」
《しっかり覚える加法定理 $$ \begin{align*} \cos(\alpha+\beta) &= \cos\alpha\cos\beta - \sin\alpha\sin\beta \\ \sin(\alpha+\beta) &= \sin\alpha\cos\beta + \cos\alpha\sin\beta \end{align*} $$
ミルカ「$\tan$ は?」
テトラ「はい、 $\tan$ の加法定理は先ほど導きましたよ! 『いち引くタンタン、タン足すタン』ですっ!(第315回参照)」
《いち引くタンタン、タン足すタン》
$$ \tan(\alpha+\beta) = \frac{\tan\alpha + \tan\beta}{1 - \tan\alpha\tan\beta} = \frac{\REMTEXT{タン足すタン}}{\REMTEXT{いち引くタンタン}} $$
僕「うん、 $\tan$ の定義を使って素直に計算したよね。《まっすぐな証明》だ」
$$ \tan\theta = \frac{\sin\theta}{\cos\theta} $$
ミルカ「ふうん……だったら複素数の積を使って《広がる証明》はどうだろう」
テトラ「三角関数の公式なのに、複素数の積を使うんですか?」
僕「おお……!」
ミルカ「複素平面に単位円を描こう。複素平面上の点と複素数を同一視するとして、この点 $z$ に対応する複素数は何か」
点 $z$ に対応する複素数は?
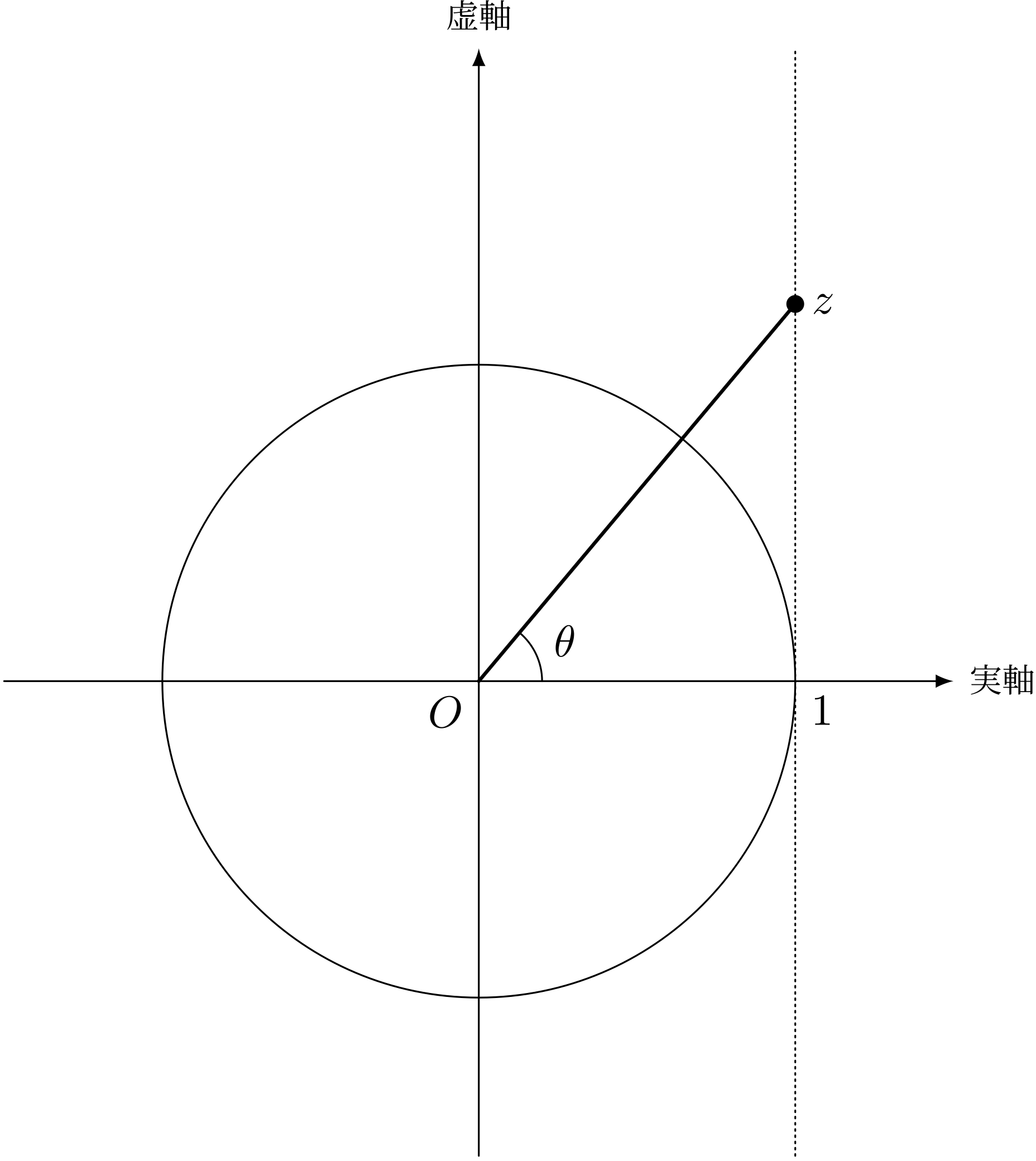

僕「これは……はい、テトラちゃん」
テトラ「はい。原点から見上げるようすを考えて……縦方向は $\tan\theta$ ですから、複素数としては、 $$ z = 1 + (\tan\theta)i $$ ですよね?」
僕「そうだね。 $\tan\theta i$ としなかったのは……」
テトラ「はい、 $\tan(\theta i)$ と紛らわしくなるからです」
ミルカ「カッコでくくるのは面倒だから、虚数単位を前に書くことにしよう。つまり、こうだ」 $$ z = 1 + i\tan\theta $$ 僕「ああ、こういう表記、本でもときどきあるね。複素数を $a + ib$ と書くような」
点 $z$ に対応する複素数
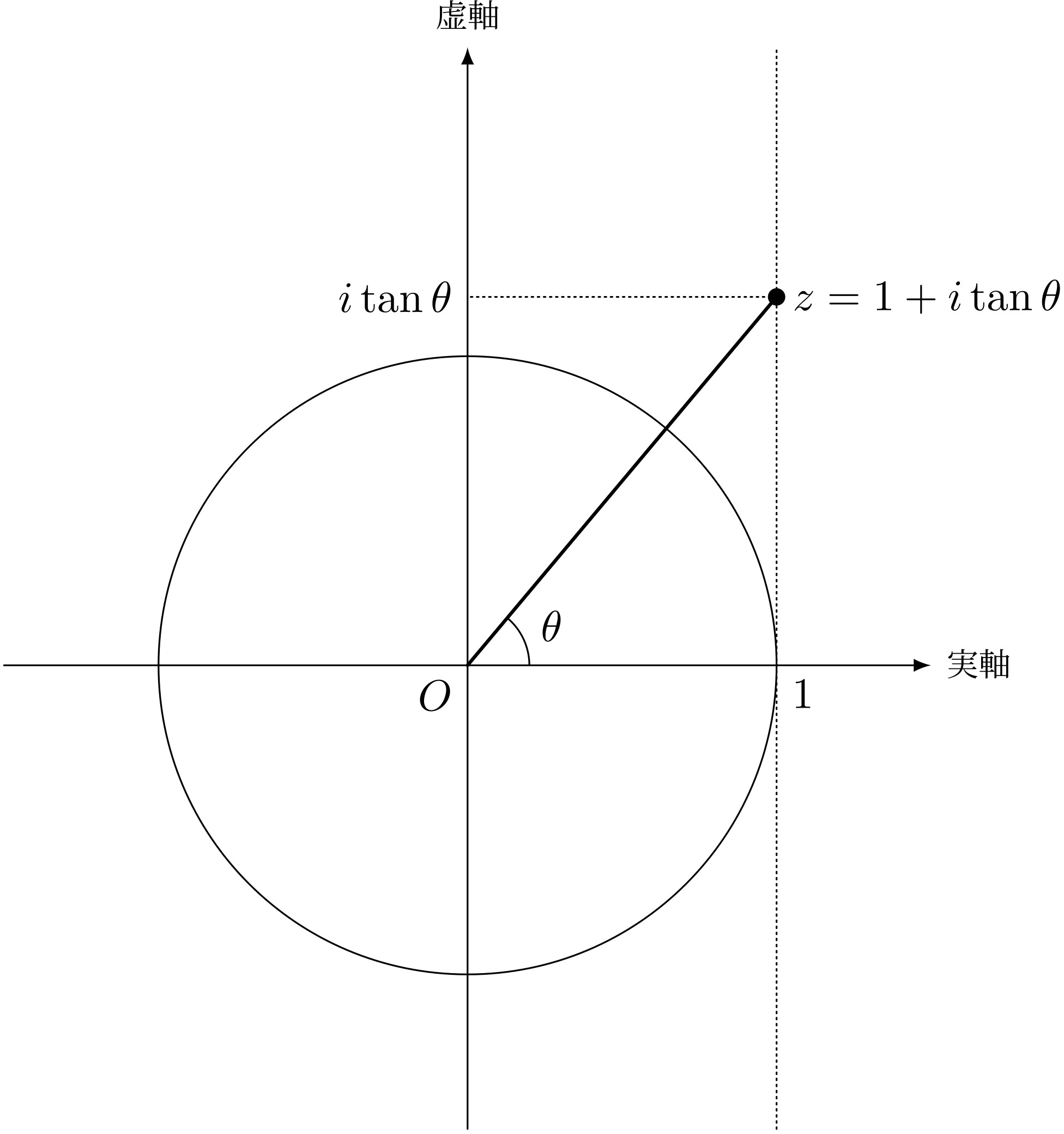
テトラ「そうなんですね。ところでこれが加法定理になるんですか?」
ミルカ「二個の複素数をこのように定義する。偏角をそれぞれ $\alpha,\beta$ とする」 $$ \begin{align*} z_1 &= 1 + i\tan\alpha \\ z_2 &= 1 + i\tan\beta \end{align*} $$ 僕「こういうことだね」
二個の複素数を考える
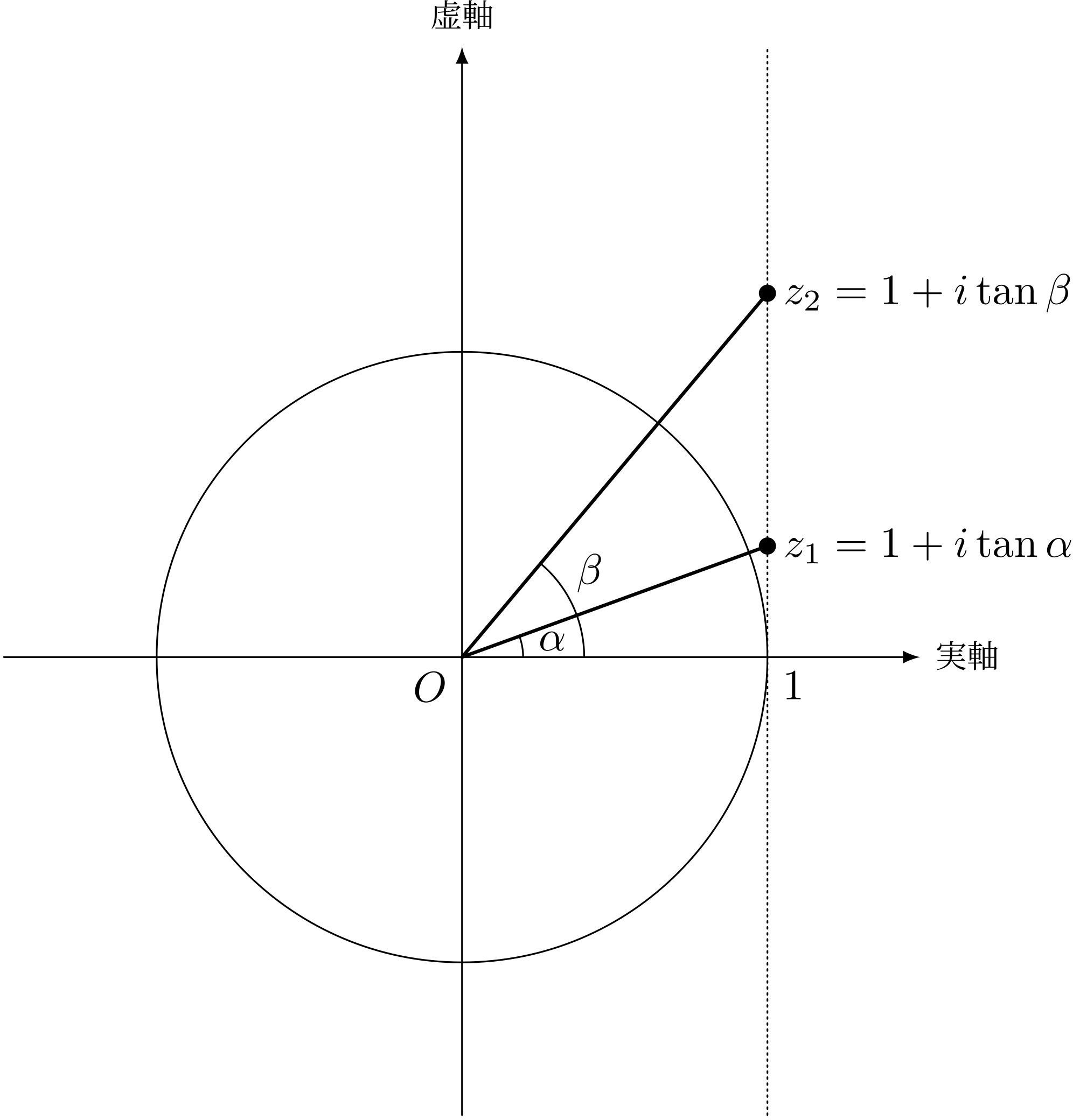
ミルカ「そう。君にはもう話は見えているんだろう?」
僕「うん。同じ方法で $\cos,\sin$ の加法定理を計算したこともあるよ(『数学ガールの秘密ノート/複素数の広がり』参照)」
テトラ「お待ちください。あたしもそれは見ていましたよね?」
僕「そうだね」
テトラ「二つの複素数の積を計算して……確かふつうに展開すればよかったはずです。あたし、計算してみます」 $$ \begin{align*} z_1z_2 &= (1 + i\tan\alpha)(1 + i\tan\beta) && \textbf{$z_1,z_2$の定義そのままです} \\ &= (1 + i\tan\alpha) + (1+i\tan\alpha)(i\tan\beta) && \textbf{展開前半} \\ &= 1 + i\tan\alpha + i\tan\beta + i^2\tan\alpha\tan\beta && \textbf{展開後半} \\ &= 1 + i\tan\alpha + i\tan\beta - \tan\alpha\tan\beta && \textbf{$i^2 = -1$ですから} \\ &= (1 - \tan\alpha\tan\beta) + i(\tan\alpha + \tan\beta) && \textbf{実部と虚部をまとめました} \\ &= \REMTEXT{……ええと?} \\ \end{align*} $$
ミルカ「出てきた」
僕「出てきたね」
テトラ「何がですか?」
僕「いち引くタンタン、タン足すタン」
$$ z_1z_2 = (\underbrace{1 - \tan\alpha\tan\beta}_{\REMTEXT{いち引くタンタン}}) + i (\underbrace{\tan\alpha + \tan\beta}_{\REMTEXT{タン足すタン}}) $$テトラ「ほんとですね!……って、あれ? でも、どうしてですか? いま考えたいのは《加法定理》ですよね。どうして和じゃなくて積を考えるんでしたっけ?」
僕「複素数では《積の偏角は、偏角の和》になるからだね。 $2\pi$ の整数倍は同一視するとして」
テトラ「あっあっ、そうでした! この例でいうと……こうなりますね」 $$ \begin{array}{cc} 複素数 & 偏角 \\ \hline z_1 & \alpha \\ z_2 & \beta \\ z_1z_2 & \alpha + \beta \end{array} $$ 僕「そういうこと、そういうこと」
テトラ「ええと……《積の偏角は、偏角の和》はわかっているつもりなんですが、それと、この $z_1z_2$ の関係がよくわからないです。理解が遅くてすみません」
$$ z_1z_2 = (1 - \tan\alpha\tan\beta) + i (\tan\alpha + \tan\beta) $$ミルカ「だったら時間を掛けよう」
テトラ「え?」
ミルカ「複素数の積の偏角が、それぞれの複素数の偏角の和になることはわかっている。それから $z_1z_2$ がこの値になることもわかっている。しかし、それが加法定理とどう関係しているのかがわからない。理解が遅いからとテトラは言う」
テトラ「……はい」
ミルカ「だったら時間を掛けよう。考える時間を掛けよう。テトラはいま理解のゴール直前にいる。テトラはここまで走ってきたのだ。だったら、自分で走り抜けてテープを切りたいだろう?」
僕「いくらでも待ってるよ」
テトラ「わかりました。考えますっ! 《なるほどのテープ》を自分で切りますっ!」
$z_1z_2$ から加法定理を導こう


僕たちは沈黙に入り、しばらくそれぞれの思考に集中した。
テトラちゃんは何か図を描き出したようだ。
僕「……」
ミルカ「……」
テトラ「わかっ、わかりましたっ! なるほどですっ!」
僕「わかった?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2021年2月19日)