![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
いまは放課後。ここは高校の図書室。
僕は書架のあいだを歩きながら本の背表紙を眺めていた。と、後輩のテトラちゃんがひょいと顔を出す。
テトラ「せーんぱいっ!」
僕「ああ、テトラちゃん」
テトラ「先輩、クイズです。すぐに答えてくださいね」
僕「いきなりのテトラクイズだね。どういう問題?」
テトラ「$\cos(\theta + \pi/4)$ を求めてくださいっ!」
僕「ええと、求めるっていうのは?」
テトラ「あっと、失礼しました」
テトラクイズ
$\cos\theta\REMTEXT{と}\sin\theta$を使って、 $$ \cos\PS{\theta+\frac{\pi}{4}} $$
を表してください。
僕「なるほど。うん、これは加法定理を使えば一発だよね。あっちの机で書いてもいい?」
テトラ「先輩、せんぱい。暗算してくださいよう! あ・ん・ざ・ん!」
僕「暗算? そういうチャレンジなのね、はいはい、ええと……」
僕は、加法定理の式を思い浮かべる。
僕「……うん、 $1/\sqrt2$ でくくれば、こうだね。くくらなくてもいいけど」
テトラクイズへの答え
$$ \cos\PS{\theta + \frac{\pi}{4}} = \frac{1}{\sqrt2}\PS{\cos\theta - \sin\theta} $$
テトラ「やっぱりサッとできちゃうんですね……」
僕「まあこのくらいはできるよ。基本的な三角関数トレーニングはしてるからね(『数学ガール/ポアンカレ予想』参照)」
テトラ「あたしも最近、三角関数の公式を練習していますが、難しいですよね。先輩はこの $\cos(\theta + \pi/4)$ はどういうふうに計算したんですか?」
僕「いや、ふつうに加法定理を使っただけだよ。 $\cos(\alpha + \beta)$ はこうなるよね。これは覚えている」
$$ \cos(\alpha + \beta) = \cos\alpha\cos\beta - \sin\alpha\sin\beta $$テトラ「はい」
僕「それから、有名角の三角関数の値も覚えている。この場合は $\pi/4$ つまり45度のコサインとサイン」
$$ \left\{ \begin{align*} \cos\frac\pi4 = \frac1{\sqrt2} \\ \sin\frac\pi4 = \frac1{\sqrt2} \end{align*} \right. $$テトラ「はいはい、そうですね。それもサッと出るんですか……」
僕「うん。もちろん覚えているんだけど、 単位円周上の点が45度にあるところを想像すれば、 $\cos\pi/4 = \sin\pi/4 = 1/\sqrt2$ になるのは軽くチェックできる。 一つの角度が45度になる直角三角形は直角二等辺三角形ということで、 対角線の長さが1になっている正方形の一辺の長さになるからね」
一つの角度が $\pi/4$ の直角三角形は直角二等辺三角形になる
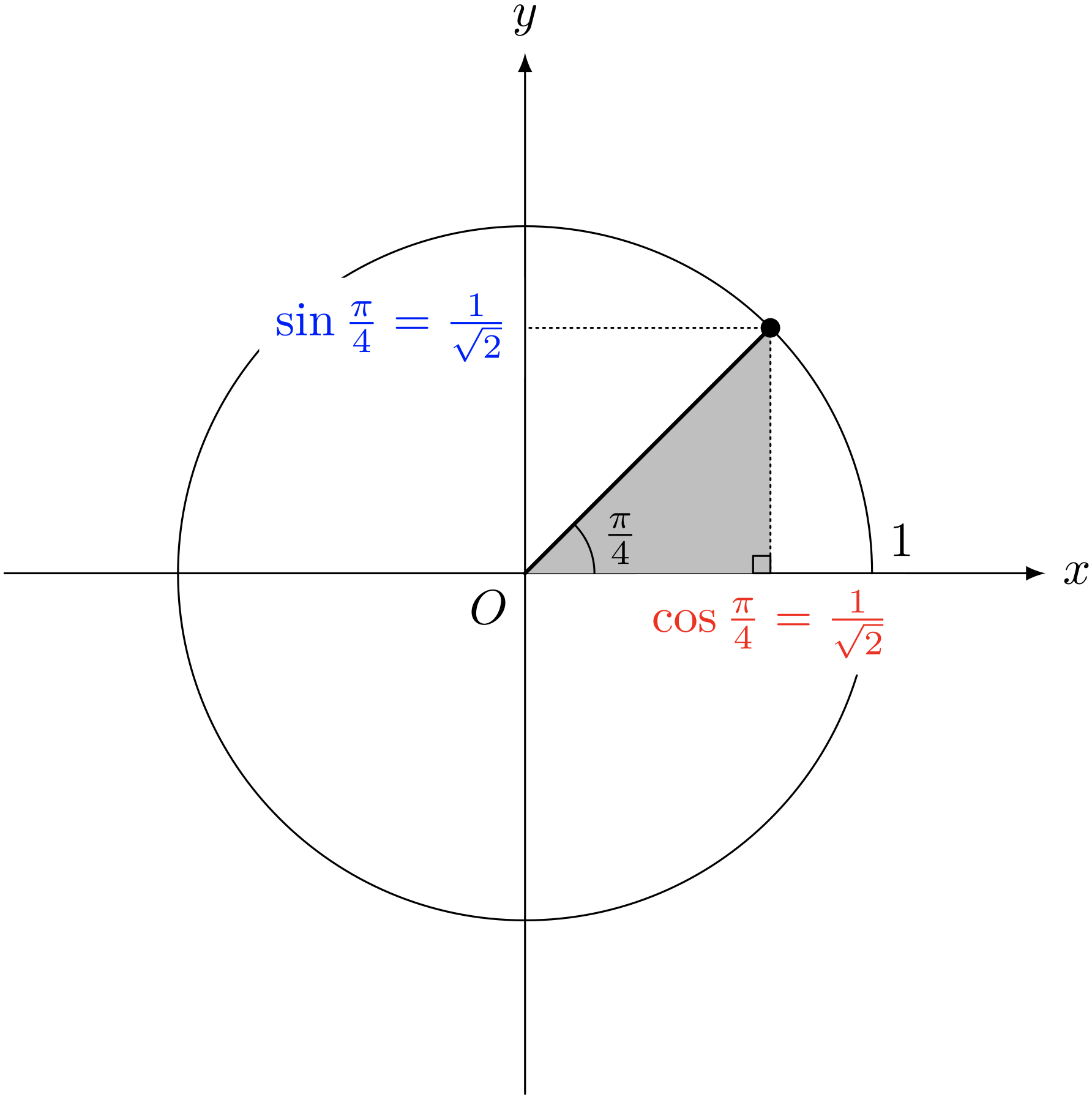
テトラ「確かにそうですね。三平方の定理で、 $$ \PS{\frac{1}{\SQRT2}}^2 + \PS{\frac{1}{\SQRT2}}^2 = 1^2 $$ ということですね?」
僕「そうそう。この場合は二辺がたまたま $\cos\pi/4 = \sin\pi/4 = 1/\sqrt2$ で等しいからくくって答えたんだ。 くくらなくても正しいけど}
$$ \begin{align*} \cos\PS{\theta + \frac\pi4} &= \cos\theta\cos\frac\pi4 - \sin\theta\sin\frac\pi4 && \REMTEXT{加法定理から} \\ &= (\cos\theta)\frac1{\sqrt2} - (\sin\theta)\frac1{\sqrt2} && \REMTEXT{$\cos\pi/4 = \sin\pi/4 = 1/\sqrt2$から} \\ &= \frac1{\sqrt2}(\cos\theta - \sin\theta) && \REMTEXT{$1/\sqrt2$でくくった} \end{align*} $$テトラ「先輩のおっしゃることはよくわかります。 テトラもいちおうその計算はできるんですが、サッと出てきません。練習でしょうか?」
僕「そうだね。有名角の値や加法定理はよく練習して損はないよね。 有名角の値はほんの数個だけだからすぐに覚えられるし、単位円を思い浮かべればすぐにチェックできる。 分数で混乱しないように注意しないといけないけど」
テトラ「有名角は $\pi/6, \pi/4, \pi/3$ とか?」
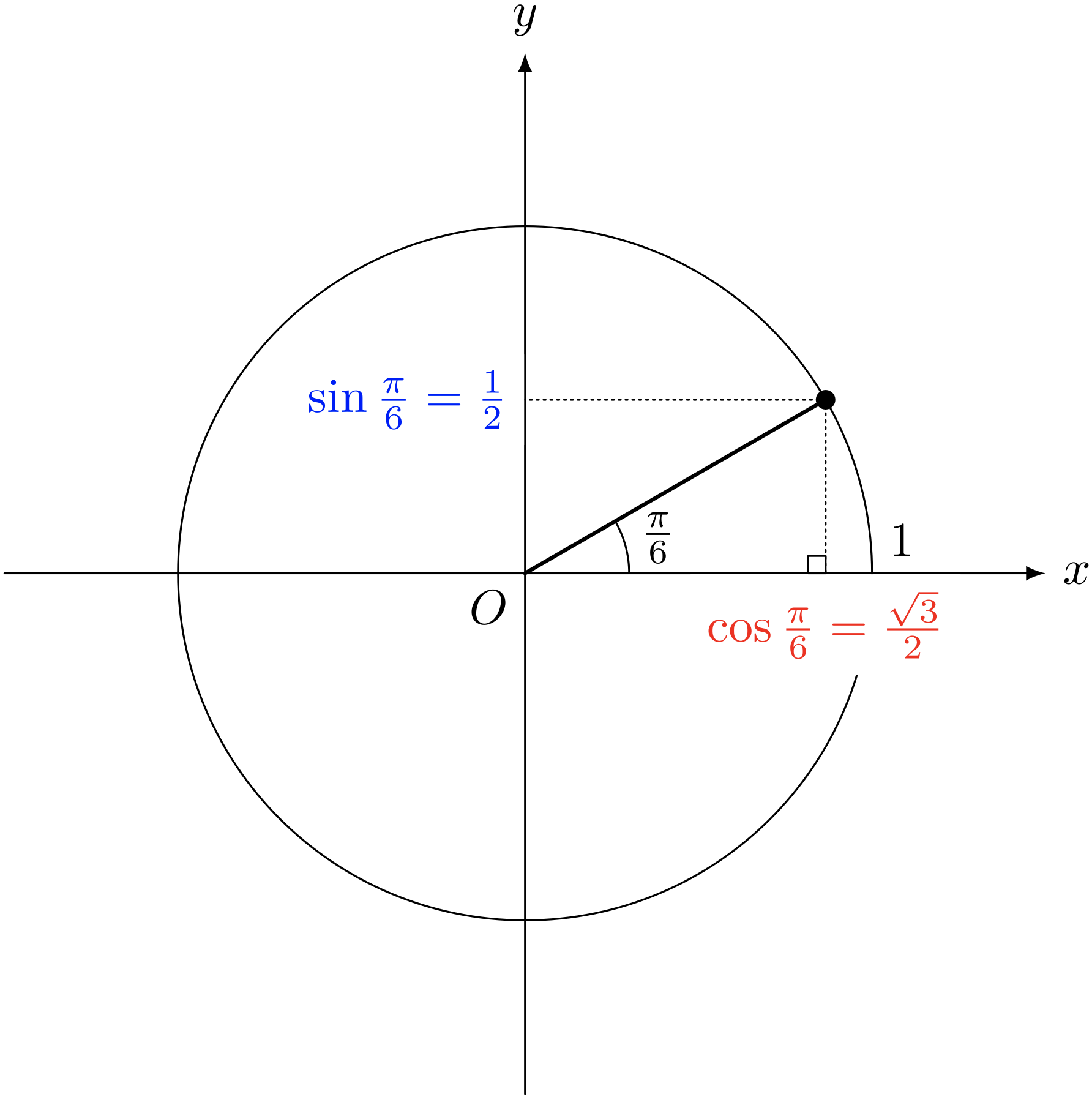
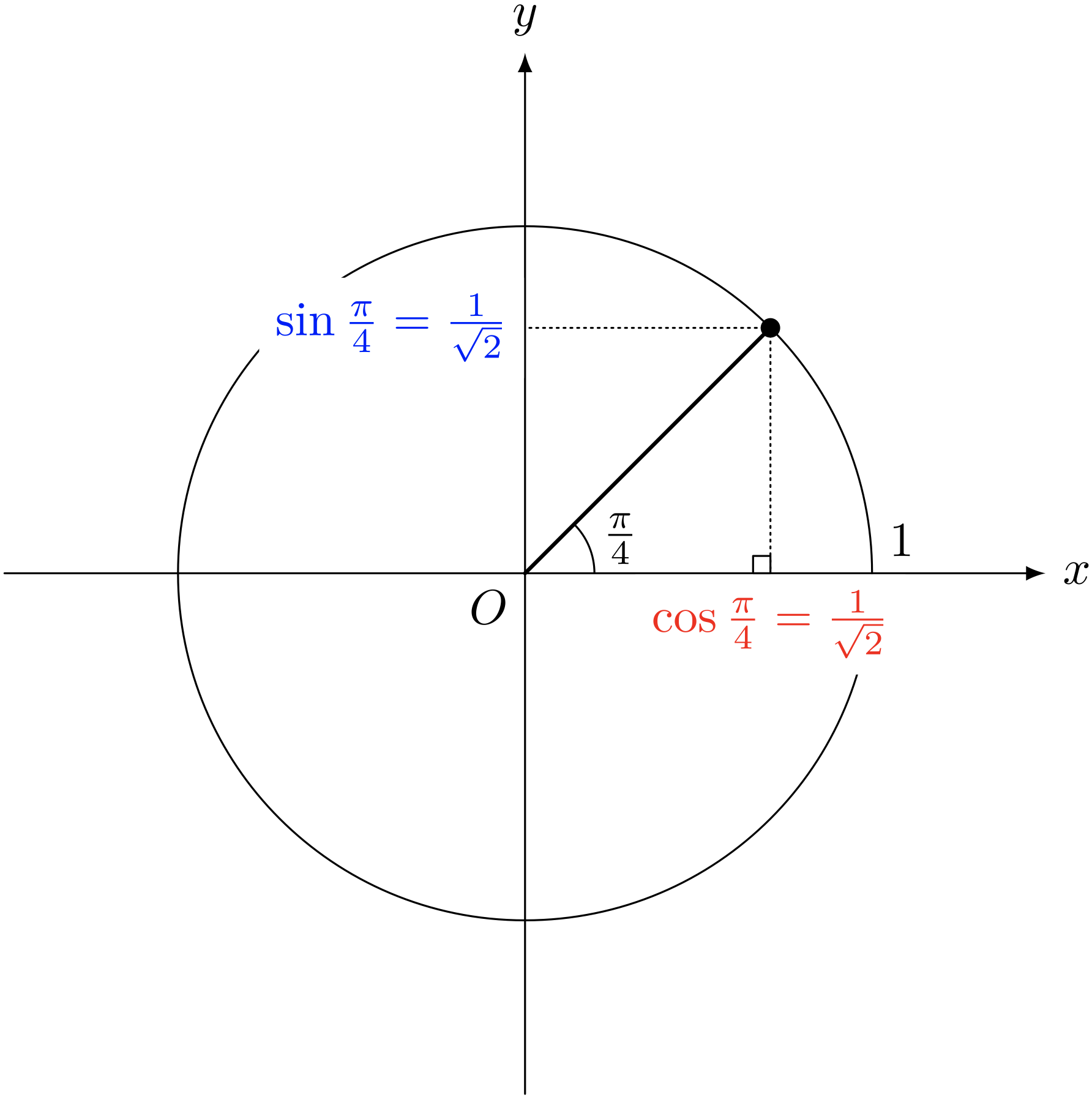
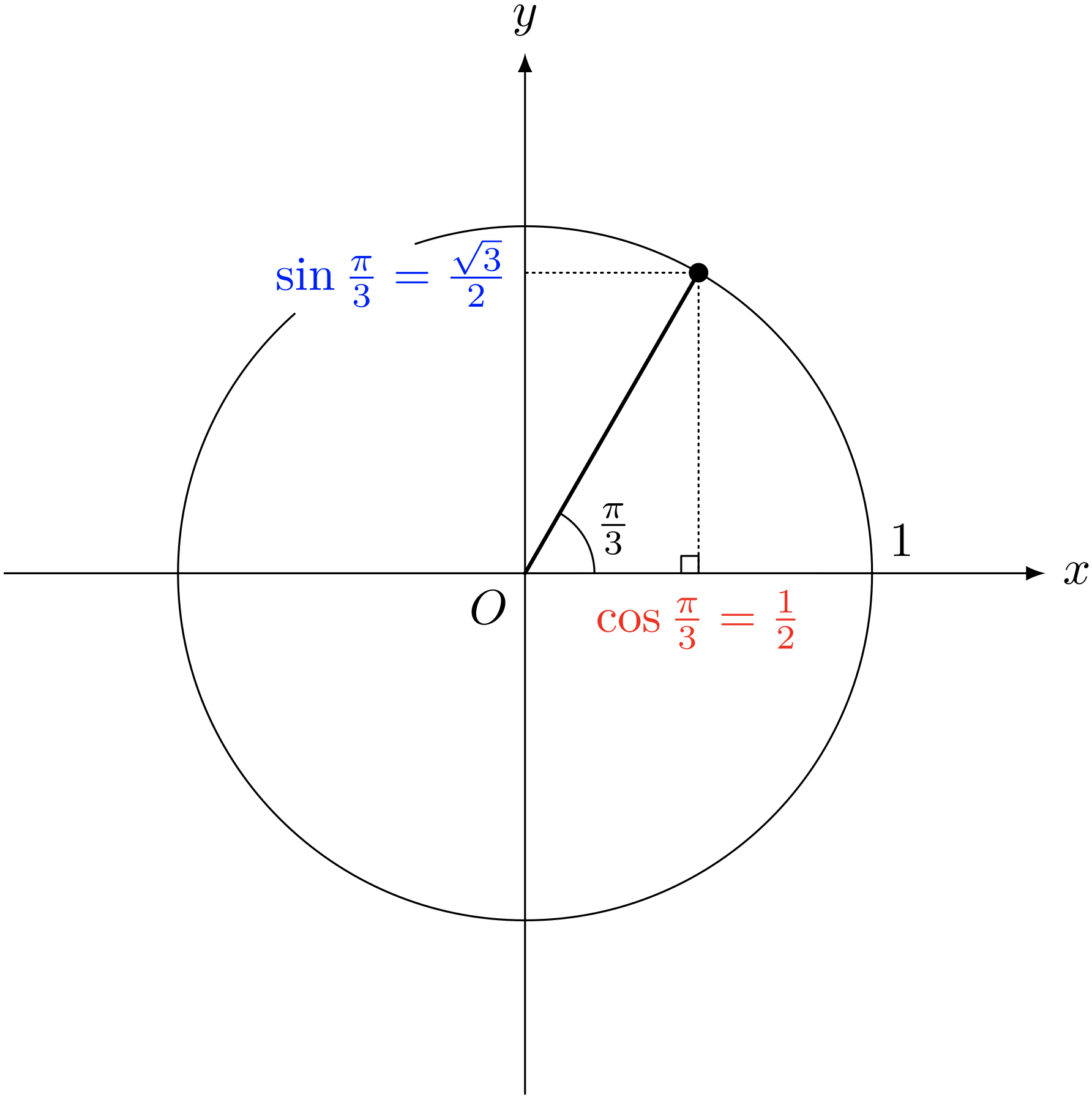
僕「うん、それから $0, \pi/2, \pi$ もいちおうね」
テトラ「なるほど」
僕「その他に $2\pi/3, 3\pi/2$ も練習すると楽しいけど、それは暗記というよりも単位円を思い浮かべる練習になるかな」
テトラ「練習って暗記カードを作るんですか? 表に $\cos\pi/3$ と書いてあって裏に $1/2$ と書いてあるみたいな」
僕「それでもいいけど、録音してもいいよね」
テトラ「録音?」
僕「自分の声で $\cos\pi/3$ と録音して、数秒あいだをあけて $1/2$ と録音する」
テトラ「なるほどですっ! それを使ってトレーニングするんですか」
僕「ゲーム感覚だよね。あとは友達と問題を出し合うのも練習になるかな」
テトラ「問題を出し合うのは楽しそうですね。問題。 $\cos\pi/2$ イコール?」
僕「ゼロ。そうそう、そういう具合に問題を出すんだ」
$$ \cos\frac\pi2 = 0 $$テトラ「はい」
僕「問題。 $\sin\pi/2$ イコール?」
テトラ「えとえと、点が上に来るから……えっと、1です!」
僕「はい、正解です」
$$ \sin\frac{\pi}{2} = 1 $$テトラ「いきなり言われるとドキドキしちゃいますね。問題。 $\cos2\pi/3$ イコール?」
僕「$-1/2$ だね」
$$ \cos\frac{2\pi}{3} = -\frac{1}{2} $$テトラ「先輩、速すぎですっ!」
僕「1の三乗根である $\omega,\omega^2$ の実部だから、すぐに出るよ。複素数平面で、正三角形の頂点」
$x^3 = 1$ の解
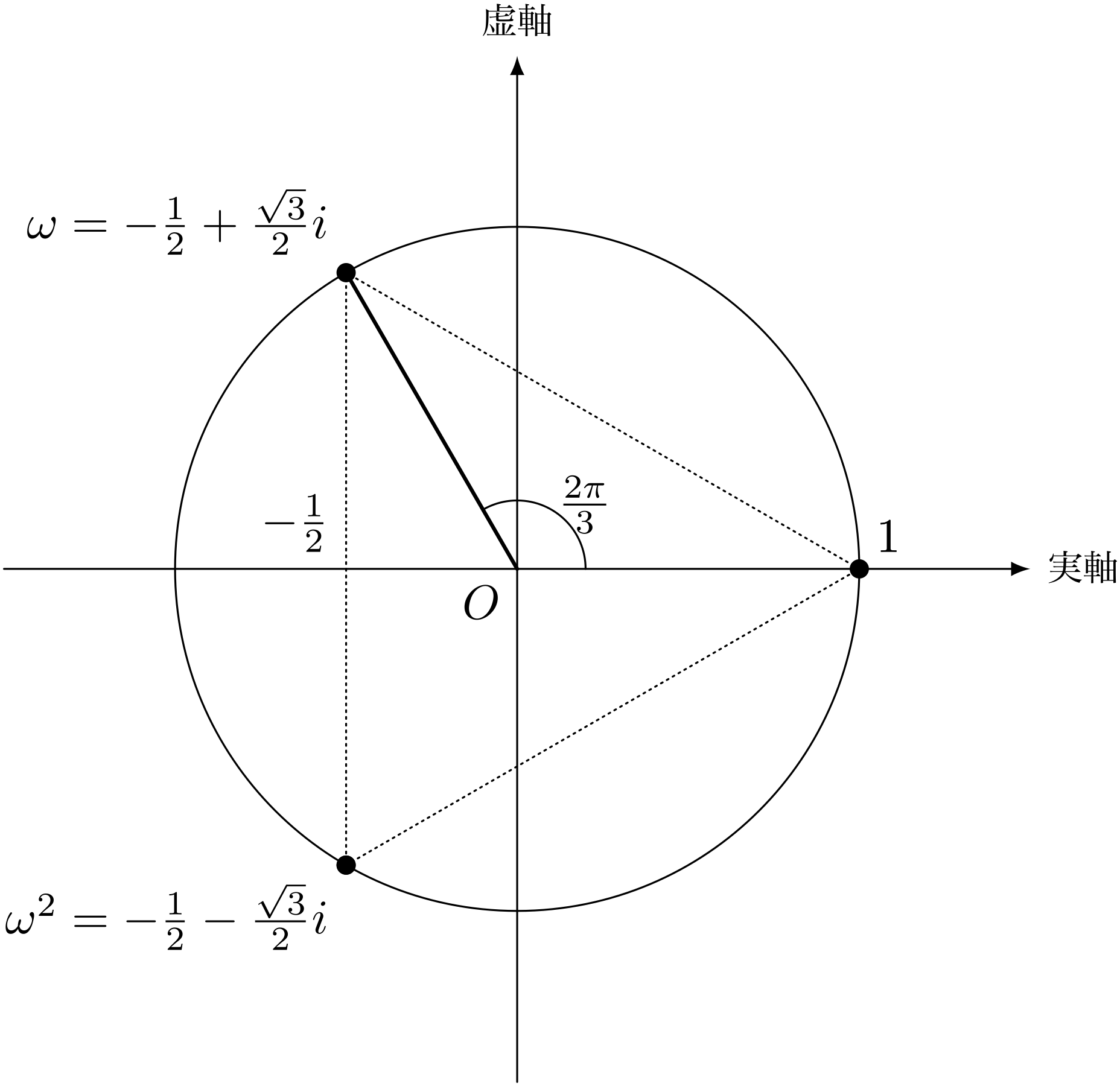
三次方程式 $x^3 = 1$ の解は、 $x = 1, \omega,\omega^2$ になる。
テトラ「なるほど……先輩は有名角の値が《お友達》になっているんですね……」
僕「お友達?」
テトラ「そうです。友達の名字を言われるとあだ名や性格がパッと思いつくみたいに」
僕「そうかもしれないね。《お友達》か……」
テトラ「有名角もそうですけれど、加法定理も練習する必要がありますよね」
僕「といっても、加法定理については二つをしっかり覚えておくと、あとは導けちゃうけど」
テトラ「《しっかり覚える加法定理》?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2021年2月5日)