![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
僕が出した問題をテトラちゃんが整理し、だいぶ計算も進んできた(第315回参照)。
問題
縦が2メートルのスクリーンがあり、その底部は座席の目の高さから1メートルの高さに設置してあります。
このスクリーンを《見込む角》をできるだけ大きくするためには、スクリーンから何メートル離れればいいでしょうか。

※少年のイラストは「いらすとや」さんから
テトラ「《見込む角》と《見上げる角》をそれぞれ $\theta,\alpha$ として、タンジェントの加法定理を使って整理するとこうなりました。 $$ \tan\theta = \frac{2x}{x^2 + 3} $$ ああああっ! やっぱり駄目ですっ!」
僕「ど、どうしたの? 合ってるよ?」
テトラ「$\theta$ を最大にするんですよね?」
僕「そうそう。《見込む角》を最大にするような、 $x$ の値を求める。 だからこの式を得たのはとても大きな成果だよ。だって、 $$ \tan\theta = \REMTEXT{《$x$の関数》} $$ という形になったから」
テトラ「でも、ここからどうやって、 $$ \theta = \REMTEXT{《$x$の関数》} $$ という形にするんでしょう?」
僕「もちろんそれは $\tan$ の逆関数を使えばできるけど、そこまで考える必要はないよ。だって……」
テトラ「お待ちください。 $\theta = $ じゃなくてもかまわないということですよね……ちょっと考えさせてください」
僕「ああ、うん、もちろんどうぞ」

テトラ「……あたしはこんなふうに考えました」
僕「うん、それはとても正しい道筋だと思うよ」
テトラ「ですよね。そしてその《$x$ の関数》がどんなふうに増えて、どんなふうに減るかを調べるんだと思ったんです。そうです。そうやって最大値を求めるんです」
僕「念のために言うけど、いま知りたいのは、
$\theta$ の最大値
じゃなくて、
$\theta$ が最大値を取るときの、 $x$ の値
だよ」
テトラ「あっ、そうです。あたしが言いたかったのはそっちです。あたしって、自分が思っていないことを口走っていますね……」
僕「いやいや、まあまあ」
テトラ「いま、あたしたちが手に入れたのは、 $$ \tan\theta = \frac{2x}{x^2 + 3} $$ という式です。この式は $x > 0$ のときにいつも成り立ちます」
僕「うん、そうだね」
テトラ「でもこの式ではまだ、 $x$ の値が決まったとしても $\tan\theta$ の値しかわかりませんよね。 だとしたらどうやって $\theta$ の最大値がわかるんでしょう」
僕「テトラちゃん、テトラちゃん。ほらほら、またまた。 いま知りたいのは $\theta$ の最大値じゃないよね?」
テトラ「あっ、また……あたしたちは、 $\theta$ を最大にするような $x$ の値を求めているんでした。 それがあたしたちの目的です。 あたし、何か大きな勘違いしてます?」
僕「$\tan\theta$ の値は、 $x$ の値が決まればわかる。 それを考えれば僕たちの目的は達成することができるよ。 $\tan$ がどういう関数であるかを考えればわかる」
テトラ「$\tan$ がどういう関数であるか……どういう関数なんでしょう」
僕「たとえば、 $0 \leqq \theta < \pi/2$ の範囲で考えたとき、 $y = \tan\theta$ はどんなグラフになるかわかる?」
テトラ「はい、わかります。 $0$ から始まっていくらでも増えていきますね」
$0 \leqq \theta < \pi/2$ での $y = \tan\theta$ のグラフ
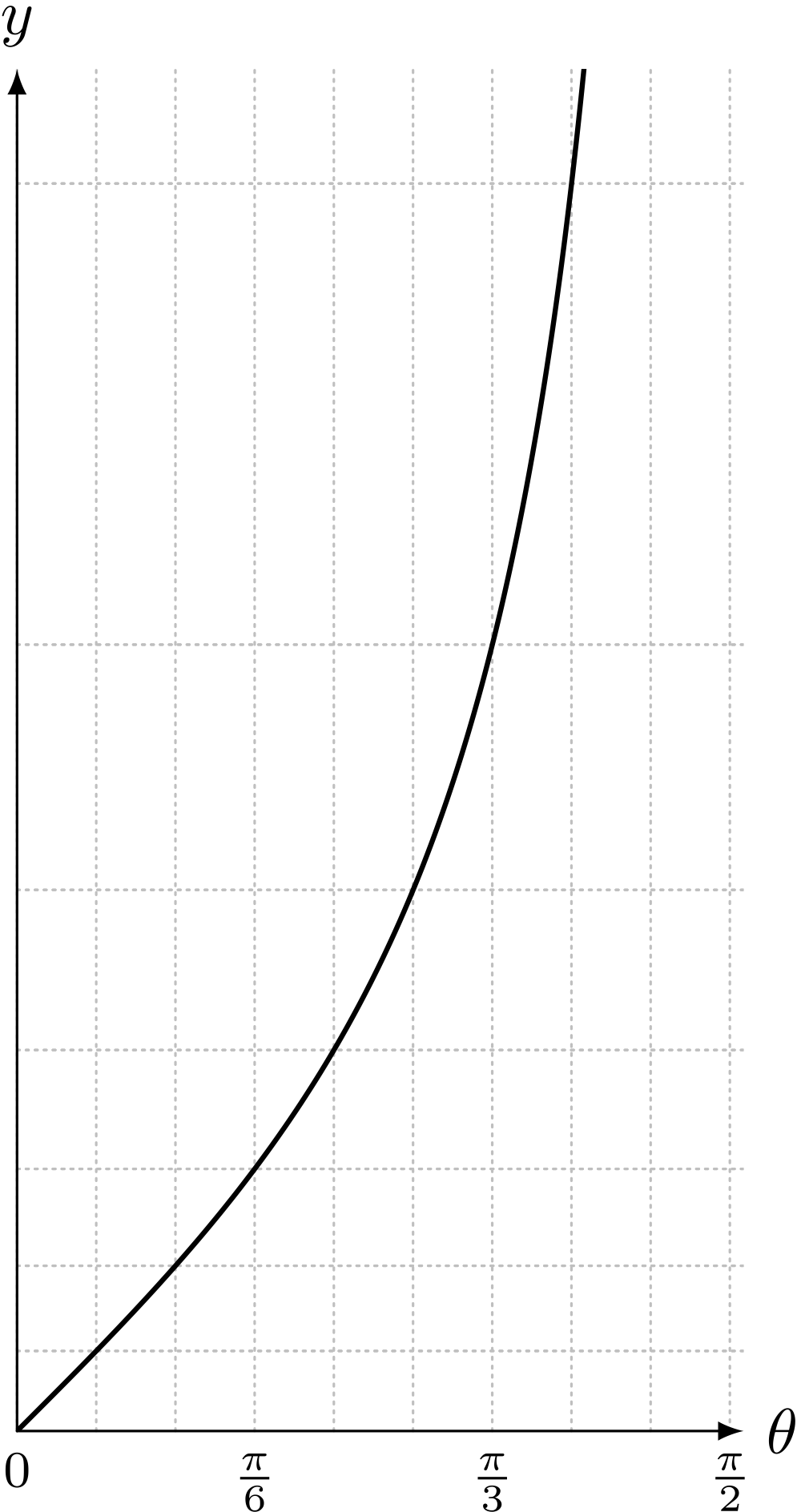
僕「そうそう。単調増加しているわけだ」
テトラ「単調増加……あっ、わかりましたっ! 先輩のおっしゃっていることがわかりました。 $\tan\theta$ が最大値を取るとき、 $\theta$ も最大値を取るんですねっ!?」
僕「それそれ」
テトラ「ああああっ、そうですよねえっ! だったら、 $$ \tan\theta = \frac{2x}{x^2 + 3} $$ を考えればいいということになりますね……」
僕「うん、だから、 $x > 0$ として、 $$ f(x) = \frac{2x}{x^2 + 3} $$ という関数 $f$ を考えればいいんだね。そしてこの関数 $f$ が最大値を取る $x$ を求めるのが僕たちの新たな目標ということになる。うん、分母はゼロにならないし」
テトラ「わかりました。 $f(x)$ が最大値を取る $x$ を求めれば、自動的にそれは $\theta$ を最大にする $x$ になります」
僕「テトラちゃんは、関数 $f(x)$ が最大値をとるときの $x$ を求めよと言われたら、どうする?」
テトラ「あ、あのですね。び、微分しようと思います」
僕「そうだね。微分するのは関数を調査する定番の方法だけど、それはどうして?」
テトラ「微分するというのは、 $y = f(x)$ のグラフで考えると、 各点での接線の傾きを求めることですよね。最大値を取るところでは、 接線の傾きがゼロになるから……ですか?」
最大値を取るところで《接線の傾き》がゼロになっている例

僕「うんうん、そうだね」
テトラ「はい」
僕「大きな流れはこれでいいし、導関数の値がゼロになる点を調べるのは大事なんだけど、注意がいくつかある。 たとえば、最大値じゃなくて最小値を取るときの場合もあるし、 極大値や極小値のときもあるし、 $x$ の範囲が区切られているときも注意がいるね。 導関数の値がゼロになるのはあくまでも接線の傾きがゼロになっているということに過ぎないから」
最大値を取るところと最小値を取るところの両方で《接線の傾き》がゼロになっている例
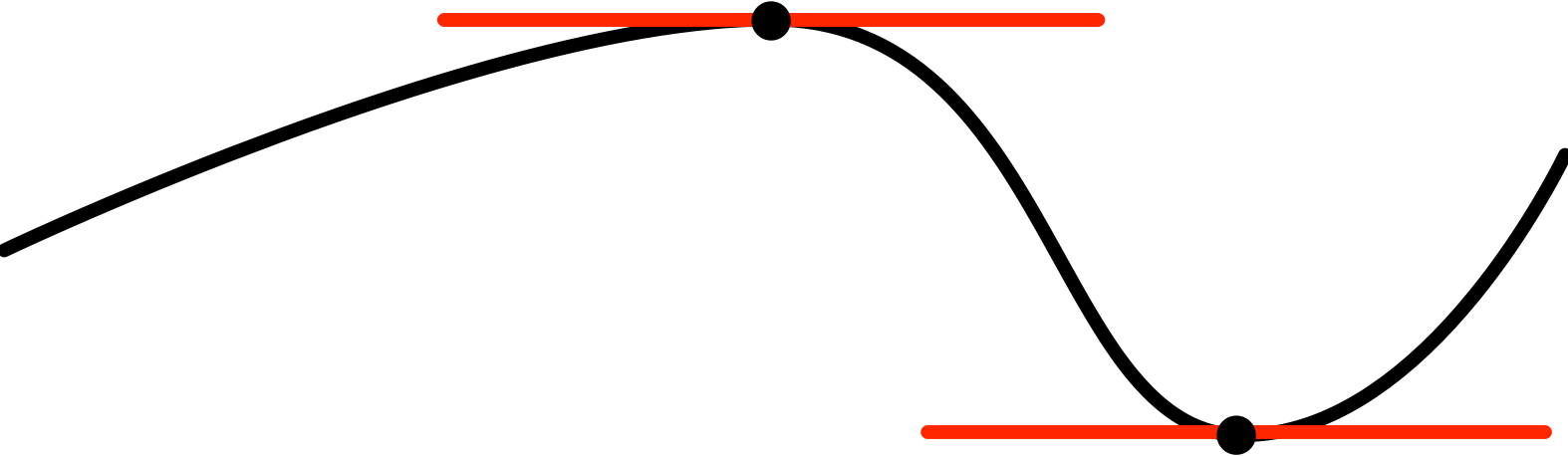
《接線の傾き》がゼロになっていても、そこでは最小値を取らないし最大値も取らない例
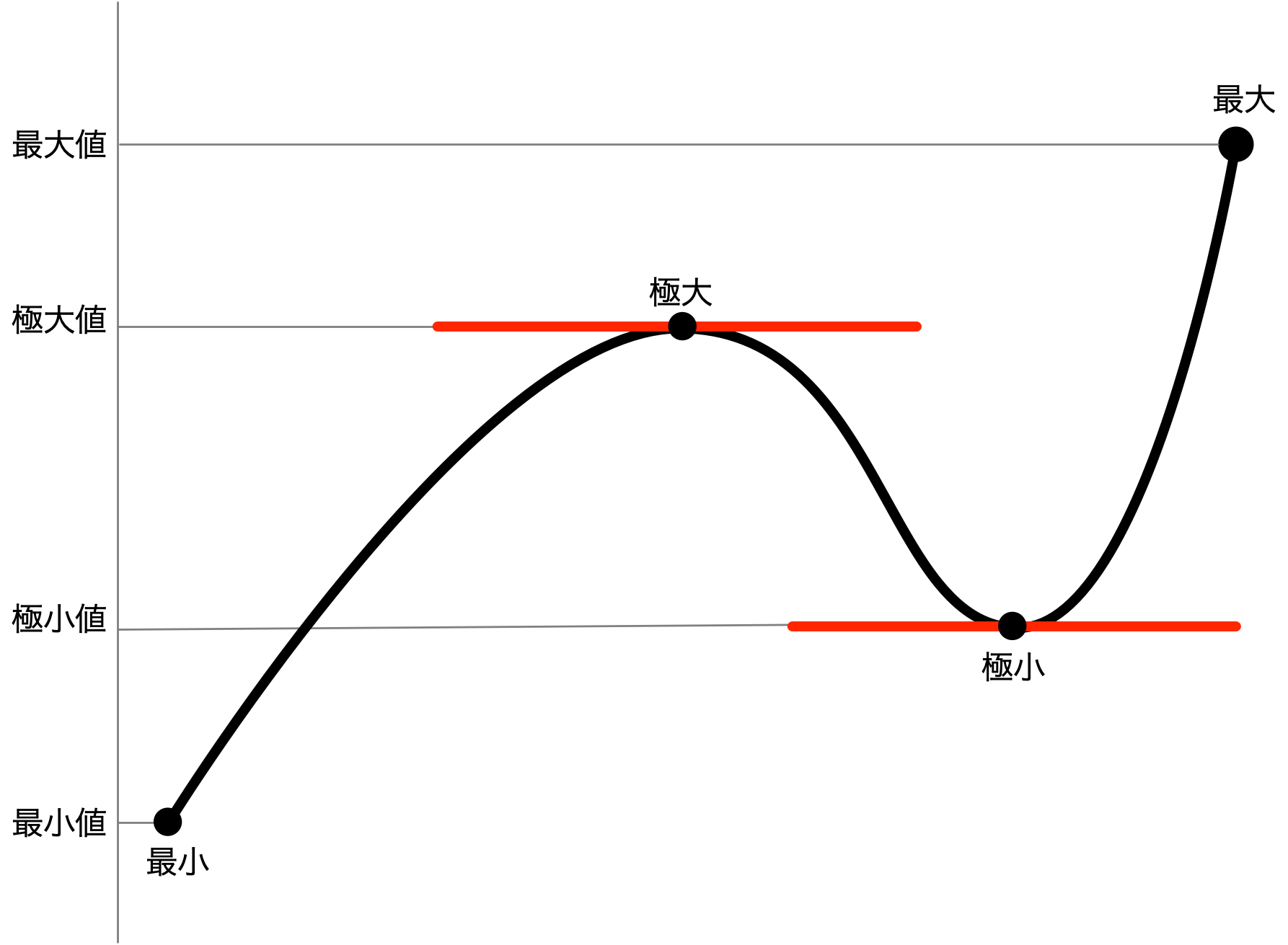
テトラ「なるほど……それは何とか理解しているつもりです。ですが……」
僕「?」
テトラ「関数 $f(x)$ を微分する方法が自信ないんです。分数関数ですよね……」
この関数を微分しよう
$$ f(x) = \frac{2x}{x^2 + 3} $$

僕「あ、そっちを気にしていたんだね。これは《積の微分》を使えば難しくないよ」
積の微分
二つの関数の積 $g(x)\cdot h(x)$ の導関数は、次のようにして求められる。 $$ \PS{g(x)\cdot h(x)}' = g'(x)\cdot h(x) + g(x)\cdot h'(x) $$
テトラ「ああ!」
僕「こんなふうに単純化した方が覚えやすいけどね」
$$ (gh)' = g'h + gh' $$テトラ「あっはい。《積の微分》はわかってました……」
僕「$f(x)$ は分数になっているけれど、それは二つの関数の積と考えられるよね」
$$ \begin{align*} f(x) &= \frac{2x}{x^2 + 3} \\ &= 2x \cdot \frac{1}{x^2 + 3} \\ &= \underbrace{(2x)}_{= g(x)}\cdot\underbrace{(x^2 + 3)^{-1}}_{= h(x)} \end{align*} $$テトラ「はいはい確かに積ですね。分母に来ているところを $-1$ 乗だと考える!」
$$ \frac{1}{x^2 + 3} = (x^2 + 3)^{-1} $$僕「これで $f$ を微分できるかな……」
テトラ「積の微分に当てはめてみます!」
僕「お願いします(ぺこり)」
テトラ「うけたまわりました(ぺこり)」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2021年2月12日)