![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕とユーリは、 $y = \tan\theta$ のグラフを描いていた。
いまは、ユーリが $\tan$ が持っている性質のひとつを証明したところ。
ユーリ「……ね! これで、 $$ \tan(\KAKUDO{90} - \alpha) = -\tan(\KAKUDO{90} + \alpha) $$ がいえたよ!」
僕「そうだね。大正解! これで証明ができたね!(第313回参照)」
こんなふうにわいわい話しながら、僕とユーリはタンジェントをたっぷりと楽しんでいった。
僕「$y = \tan\theta$ のグラフもできたことだし、ユーリに大小クイズを出そう」
ユーリ「大小クイズ? 何でもどんとこいやー!」
大小クイズ
$\alpha,\beta$ は実数とします。
また $\tan\alpha,\,\tan\beta$ が定義されているとします。このとき、 $$ \alpha < \beta \quad\REMTEXT{ならば}\quad \tan\alpha < \tan\beta $$ といえますか。
僕「さあ、どうかな?」

ユーリ「角度が大きくなれば $\tan$ は大きくなるから、いえる!」
僕「そうかな?」
ユーリ「だって、 $y = \tan\theta$ のグラフはいつも上がっていくじゃん? こんな感じで」
$y = \tan\theta$ のグラフは、いつも上がっていく(?)

僕「いつも上がっていく」
ユーリ「それに、角度が大きい方が高く見上げるわけだから、 $\tan\alpha < \tan\beta$ なのは当たり前でしょ」
僕「ファイナルアンサー?」
ユーリ「ん……ん……待って! 違う、違う! いまのなし! 90度を《またぐ》ときがあるんだね? たとえば、こーゆーの!」
$\alpha = \KAKUDO{60}, \beta = \KAKUDO{120}$ の場合
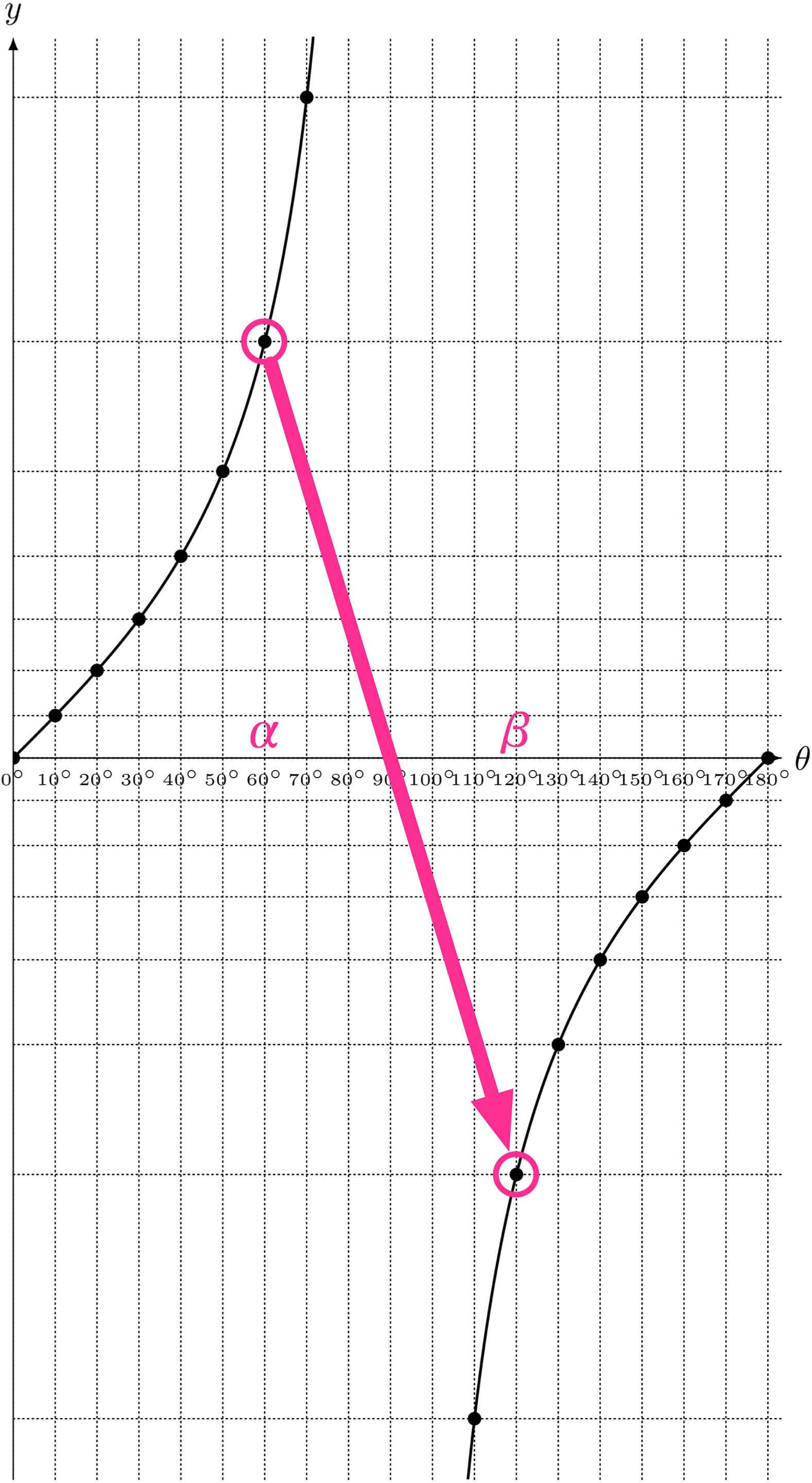
僕「うん、そうだね」
ユーリ「だから、 $\alpha < \beta$ のとき……」
僕「はい、正解。だから答えとしては《いえません》になる」
クイズの答え
$\alpha < \beta \quad\REMTEXT{ならば}\quad \tan\alpha < \tan\beta$とはいえません。
反例は、 $\alpha = \KAKUDO{60}, \beta = \KAKUDO{120}$ です。 このとき、 $$ \alpha < \beta $$ ですが、 $\tan\alpha = \SQRT3,\, \tan\beta = -\SQRT3$ なので、 $$ \tan\alpha > \tan\beta $$ となるからです。
ユーリ「ふー……あぶなかったぜ。勘違い、勘違い」
僕「ところで、ユーリは、 $$ \tan\alpha < \tan\beta \quad\REMTEXT{と}\quad\tan\alpha > \tan\beta $$ の二つの場合を書いたけど、 $\alpha < \beta$ のとき、 $$ \tan\alpha = \tan\beta $$ になることはある?」
ユーリ「角度が違うのに $\tan$ が等しいとき……あっ、あるね! もっと広げればいーんだ! たとえば、 $\alpha = \KAKUDO{-120},\,\beta = \KAKUDO{60}$ とか!」
$\alpha < \beta \,\,\REMTEXT{で}\,\, \tan\alpha = \tan\beta$になる例
($\alpha = \KAKUDO{-120},\,\beta = \KAKUDO{60}$ の場合)
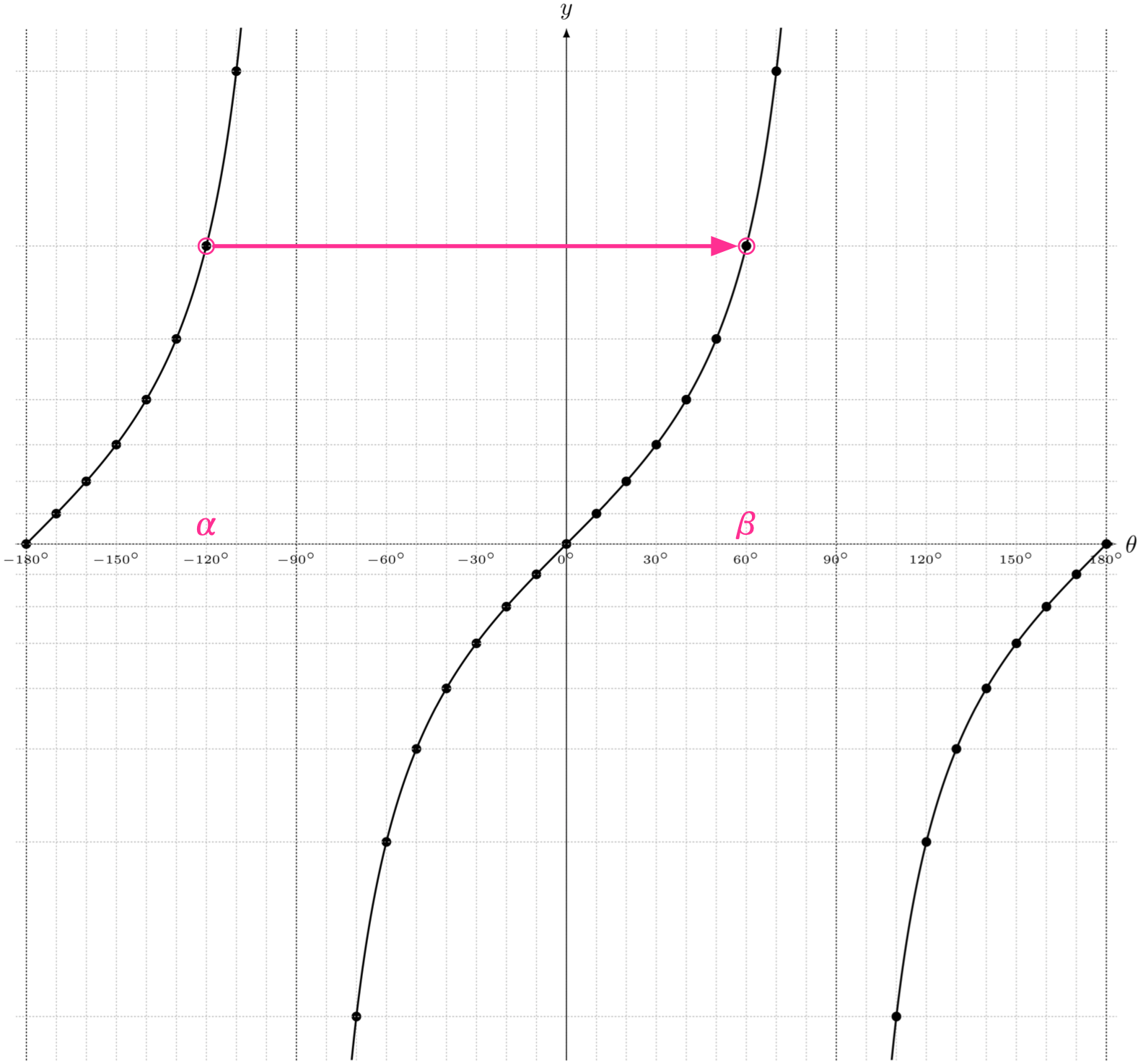
僕「そうそう、そうだね。 $\theta$ の定義域を考えればわかる」
ユーリ「むー……あのね、最初、 $$ \alpha < \beta \quad\REMTEXT{ならば}\quad \tan\alpha < \tan\beta \qquad \REMTEXT{(誤り)} $$ だって勘違いしたのはね、 $y = \tan\theta$ のグラフがつながってるところで考えたからなんだよー」
僕「そうだね。その気持ちはすごくわかる。 関数tanが連続になっている範囲ではいつも増加している。 たとえば、 $$ \KAKUDO{-90} < \alpha < \beta < \KAKUDO{90} \quad\REMTEXT{ならば}\quad \tan \alpha < \tan \beta $$ といえる」

ユーリ「-90度って、真下を向いてて、90度は真上を向いてる。だから、そのあいだについては、角度が大きくなるとtanも大きくなる」
僕「途中で減少せず、ずっと単調に増加するから、 《$\KAKUDO{-90} < \theta < \KAKUDO{90}$ で関数tanは単調増加する》っていうんだ。
ユーリ「たんちょうぞうか」
僕「途中で減少しないし、途中で等しくなることもないから、 狭義単調増加するということもある」
ユーリ「きょうぎたんちょうぞうか? 途中で等しくならないってどーゆーこと?」
僕「たとえば、 $y = f(\theta)$ のグラフがこんなふうになる関数fがあったとすると、これは狭義単調増加とはいわない」
広義単調増加だけど、狭義単調増加ではない関数の例
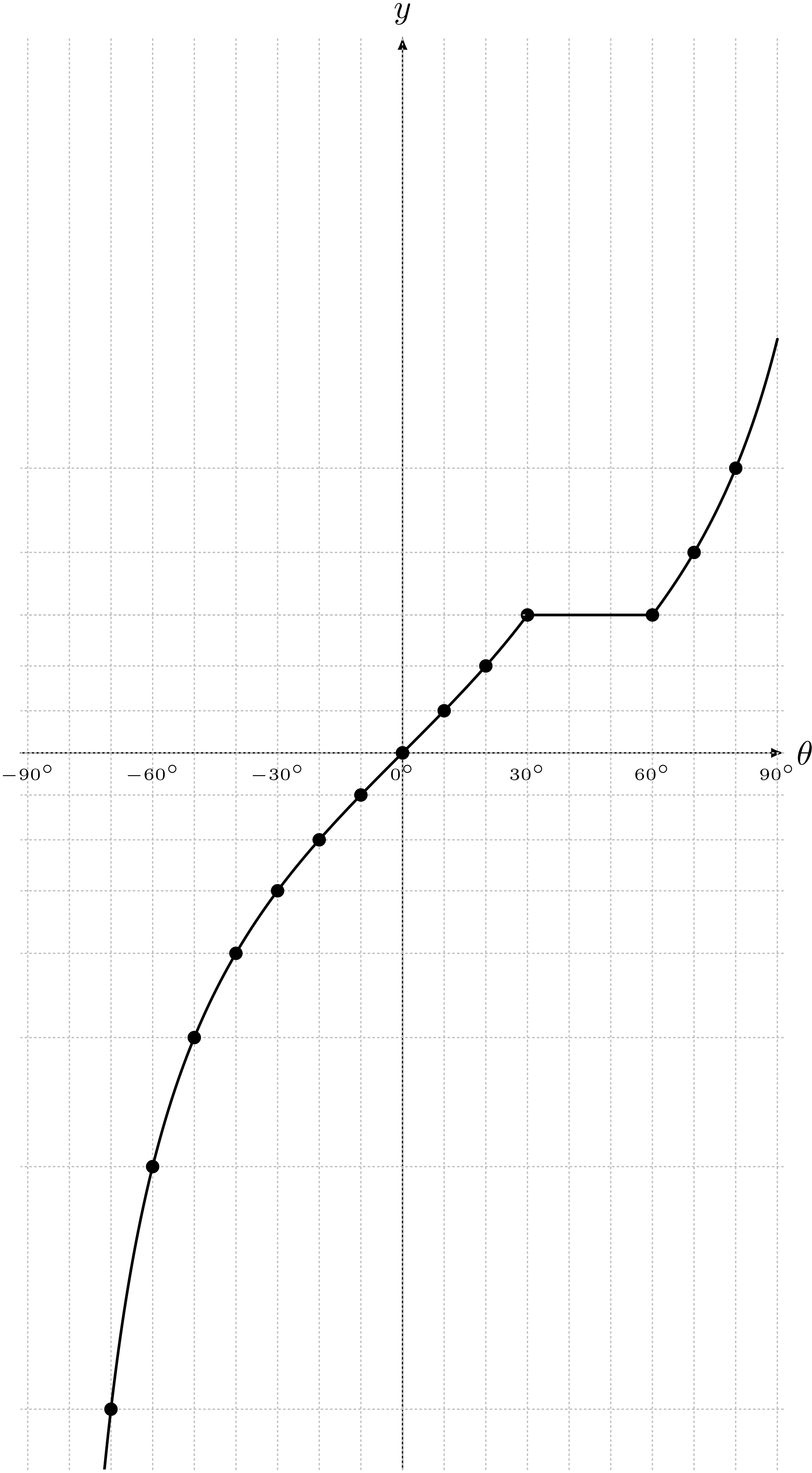
ユーリ「途中で値が等しくなるところがあるから?」
僕「そういうこと。この関数fは広義単調増加だけど、狭義単調増加ではない。$\alpha < \beta\,\REMTEXT{で}\,f(\alpha) = f(\beta)$になる場合があるから」
ユーリ「こうぎたんちょうぞうか……《こーぎ》とか《きょーぎ》とかまぎらわしくてわかんないぞー!」
僕「そうだね。ちゃんと定義を書こうか」
広義単調増加
関数fが広義単調増加であるとは、 $$ \alpha < \beta \quad\REMTEXT{ならば}\quad f(\alpha) \LEQ f(\beta) $$ が成り立つことをいいます。
※「単調増加」というと、一般にはこの意味になります。
狭義単調増加
関数gが狭義単調増加であるとは、 $$ \alpha < \beta \quad\REMTEXT{ならば}\quad g(\alpha) < g(\beta) $$ が成り立つことをいいます。
ユーリ「なーんだ、要するにイコールがつくかどうかの違い?」
僕「そういうことだね。単調増加という言葉で《減少せずに増加する》ことをいいたいんだけど、 そうすると等しくなる場合も含まれてしまう」
ユーリ「あー、だから、イコールが付くの?」
僕「そういうことだね。 それに対して、等しくはならないときの言葉を用意した。それが狭義単調増加。 《狭義》は《狭い意味では》ということ」
ユーリ「ふむふむー。理解したぜ!」
僕「関数はいろんなものの変化を考えるときに使うものだから、 増えていくか減っていくか……どんな振る舞いをするかは大事なことだよね」
ユーリ「そりゃそーだ」
僕「だから、関数の振る舞いを表す言葉があるんだよ」
ユーリ「またまた《先生トーク》炸裂だにゃ。……むむ、ちょっと待って」
そう言ってユーリは熟考モードに入った。
僕は待つ。
彼女が熟考モードに入っているあいだ、僕は静かに待つ。
窓からの光を受けて輝く、彼女の栗色の髪をながめながら。
ユーリ「もしも、関数が狭義単調増加だったら、広義単調増加?」
僕「おお!」
ユーリ「そーじゃない?」
僕「定義からすると、そうなるね。もしもある関数 $f$ が狭義単調増加だったら、それは広義単調増加といえるよ。それは論理的に正しい。なぜなら、 $$ f(\alpha) < f(\beta) \quad\REMTEXT{ならば}\quad f(\alpha) \LEQ f(\beta) $$ はいつもいえるから」
ユーリ「うんっ! だったら納得!」
僕「それを考えてたんだね」
ユーリ「それから、 $-\KAKUDO{90} < \theta < \KAKUDO{90}$ の範囲で関数tanは単調増加……狭義単調増加だよね?」
僕「そうだよ」
ユーリ「でも、全体だと?」
僕「関数tanの定義域全体で考えるということ? その場合は関数tanは単調増加じゃないよ。広義でも狭義でも。単調減少でもない」
ユーリ「あ、そっか。《どっちでもない》もアリなんだね。りょーかい!」
ユーリはすぐに『めんどくさい』って言うけれど、いざ考え始めると粘り強いんだよな。
引っかかることがあるといくらでも食い下がるし、 あれこれ納得いくまで考える。
僕も、広義単調増加や狭義単調増加という用語を聞いたとき、すぐには飲み込めなかった。
ユーリと同じように、ややこしいなと思った。 そしてさっき説明したのと同じように、 「広義」は「広い意味」で、「狭義」は「狭い意味」と考えた。
そして、本に書いてあった数学の定義と見比べて「いったい何が《広い意味》なんだろう」としばらく考えた。
腑に落ちるまではだいぶ時間が掛かったけれど、いったん納得してからはもう忘れない。
・《増加》という言葉に《等しい場合》も含めたのが、広い意味での《増加》だ。
・《増加》という言葉に《等しい場合》は含めないのが、狭い意味での《増加》だ。
それさえ納得していれば、たとえ忘れたとしても、言葉から定義を思い出すことはもう難しくない。
ユーリ「そっかーうんうん」
僕「どうした? 何か気付いた?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2021年1月29日)