![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png)
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート／図形の証明』として書籍化されています。
登場人物紹介
僕：数学が好きな高校生。
ユーリ：僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ノナ：ユーリの同級生。 ベレー帽をかぶってて、丸い眼鏡を掛けていて、ひとふさだけの銀髪メッシュ。 数学は苦手だけど、興味を持ってる中学生。
ノナとユーリと僕の三人は、図形の証明問題を題材にいろいろおしゃべりをしている（第308回参照）。
ユーリ「お兄ちゃん、他の問題出してよ」
僕「他の問題？」
ユーリ「ほれほれ、ノナも退屈しているし」
ノナ「退屈してないよう $\NONA$」
僕「うーん……じゃあ、 『三角形の外角は、その外角と隣り合っていない二つの内角の和に等しい』ことを証明してみようか。 具体的に書くと、こういう問題」
問題
図のように、三角形ABCと点Pがあります。
このとき、角ABCと角CABの大きさの和は、角ACPの大きさに等しいことを証明してください。
ユーリ「にゃるほど！ 簡単じゃん。あのね……っとっと」
ユーリは自分の考えを言いかけて、口を閉じる。
たぶん、ノナに考えてもらうための配慮をしたんだろうな。
僕「ノナちゃんは、この問題はどうかな？」
ノナ「読んでる……読んでます $\NONA$」
ノナはそういって、問題を何回か読み返す。
読みながらノナは図を指でなぞっていく。
僕「ノナちゃんは偉いね」
ノナ「$\NONAQ$」
僕「問題文に出てきた文字が、どの点に対応するかきちんと確かめているからだよ」
ノナ「読むの遅いです $\NONA$」
僕「なるほど。でも、遅くてもきちんと読むのは大事だよ。きちんと読めるならスピードを上げる練習をするのもいいけどね……ところで、 この問題はわかった？」
ノナ「はい $\NONA$」
ユーリ「じゃ、ユーリしゃべってもいい？」
僕「ユーリはもう証明までわかったの？」
ユーリ「わかってるよん。完璧さ！」
僕「完璧だったら、ちょっと待てる？ 先にノナちゃんの話を聞いてみよう。はい、ノナちゃん。どんなことを考えたか教えてください」
ノナ「こことここを足したのが……ここ $\NONA$」
ノナは、《ここ》と言いながら、図のあちこちを指さした。
僕「うん、いまノナちゃんは《証明すべきこと》が何かを言ったんだね」
ノナ「結論 $\NONAQ$」
僕「そうそう！ そうだね。結論だ。 『この問題で、証明すべきことは何ですか？』と問いかけられたら、 『角ABCの大きさと、角CABの大きさを足したら、角ACPの大きさに等しくなることです』と答えればいい」
ノナ「確かめました $\NONA$」
僕「うん、問題文を読みながら図との対応を確かめるのは大事だね」
ユーリ「名前つけてもいーよね？」
ノナ「$\NONAQ$」
ユーリ「対応いちいち確かめるの、めんどーじゃん。小文字で $a,b,c,p$ って名前を書いちゃおーよ」
僕「それはいいアイディアだね。角の大きさに $a,b,c$ という名前をつけるってことだよね。頂点の名前に合わせて」
ユーリ「そーだよー。それから角ACPは $p$ ね」
僕「ユーリは、こう考えたんだね」
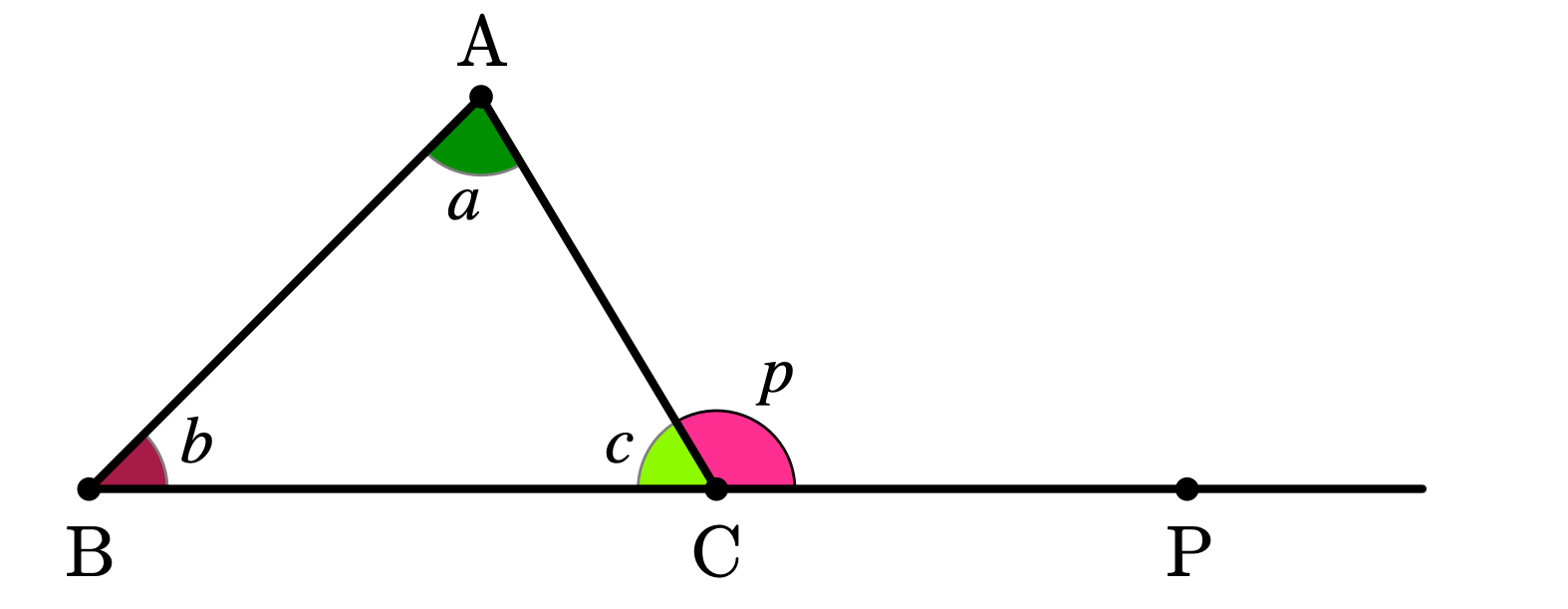
ユーリ「そーすると《証明すべきこと》は、 $$ a + b = p $$ になった！ カンタン！」
ノナ「$\NONAQ$」
僕「ユーリが言ったこと、ノナちゃんには伝わった？」
ノナ「はい $\NONAX$」
ノナは『はい』と言ったけれど、どうも何か引っかかっているように見える。
それは、彼女の自信なさそうな声でわかる。
彼女はまだ、どこかの《迷いの森》を歩いているのだ。心の中にある《迷いの森》を。
僕は、心の扉をノックする。また《先生ノナちゃん》を呼び出さなくては。
僕「（コンコン、コンコン）」
ノナ「まだ……わかってないみたい $\NONA$」
おお、反応が早い！
ノックの音だけで、ノナは自分の状態が言えるんだ！
僕「どのへんがわかってないみたい？」
ノナ「エー、ビー、シー、ピーって決めていいの $\NONA$」
ユーリ「定義は自由だよー。何でも定義すればオッケーだよー。だよね？」
僕「そうだね。『角CABの大きさを $a$ とする』のように、文字を定義するのは自由にやっていいんだよ。 それで考えやすくなったり、まちがえにくくなったりするならば、すごくいいこと。 物事がはっきりすることは、どんなことでも大歓迎なんだ」
ノナ「書かれてなくても $\NONAQ$」
僕「たとえ問題文に書かれていない文字でも使っていいよ。 自分で文字の意味を決めればね。 違うものに同じ文字を当てはめたりしてはダメだし、 あいまいな決め方をしてはダメだけど、 話がはっきりするならば、自由に決めてかまわない」
実際、そうなのだ。
高校の授業で、長い証明を書くようになって特にそれを感じる。 適切に文字を定義するなら、書く量が激減することだってある。
長い式を一文字で表せば転記ミスも減るし、書く時間も減る。式のまとまりが見やすくなることも多い。
それから……自分で文字を定義して書くことを身につけてから、教科書や参考書を読むときの意識も変わった。
本の中でどんな文字を使っているか、 どんな定義をしているかを意識するようになったんだ。
自分で考えて書くことは、誰かが書いたものを読むことにもつながっていて……
ユーリ「……ってもいーの？ ねー、いーの？」
僕「え、ごめん。何だって？」
ユーリ「ユーリの証明、もう話してもいーの？」
僕「ノナちゃんに聞いてみようよ」
ユーリ「ユーリの証明、話しても大丈夫？」
ノナ「教えて $\NONA$」
僕「じゃあ、ユーリ先生、お願いします！」
ユーリ「あいよ」
ユーリの証明
角CAB,角ABC,角BCA,角ACPの大きさをそれぞれ $a,b,c,p$ とする。
三角形の内角の和は180度だから、 $$ a + b + c = \KAKUDO{180} \qquad \cdots\cdots\REMTEXT{（ア）} $$ である。
また、 角BCPの大きさは180度だから、 $$ c + p = \KAKUDO{180} \qquad \cdots\cdots\REMTEXT{（イ）} $$ である。
（ア）と（イ）から、 $$ a + b + c = c + p $$ がいえて、 $$ a + b = p $$ が成り立つ。
したがって、 角ABCと角CABの大きさの和は、 角ACPの大きさに等しい。
（証明終わり）
ノナ「$\NONA$」
僕「なるほど。三角形の内角の和と、平角の大きさがどちらも180度であることを使ったんだね」
ユーリ「カンタン、カンタン！」
ノナ「$\NONA$」
僕「ノナちゃんはわかった？」
ノナ「合同は……合同条件は使わないんですか $\NONAQ$」
ユーリ「使わないよん。使う必要ないし」
ノナ「難しい……難しいです $\NONA$」
ユーリ「カンタンだよー。三角形の内角の和は180度じゃん？」
ノナ「わかってるよう $\NONA$」
ユーリ「それから直線になってる角は180度だし！ 図を見ればわかる」
ノナ「難しいもん $\NONAX$」
ユーリ「カンタンだって！」
ノナ「ユーちゃんみたいにtmykns……やっぱり、難しい $\NONAEX$」
僕「いやいや、二人ともちょっと待った。難しいかどうか、簡単かどうかを言い合ってもしょうがないよ。 ノナちゃんは、ユーリの証明を理解できているし、 そこに出てきた三角形の内角の和や、平角のことも理解しているようだよ」
ユーリ「そーなの？」
ノナ「わかってるよう $\NONA$」
僕「えっとね、ノナちゃんが《難しい》といってるのは、どういう意味だろう」
ノナ「$\NONAQ$」
僕「ノナちゃんは『難しい』という言葉を《外》に出してくれた。僕たちにはその言葉がちゃんと聞こえた。 では、そのときノナちゃんの《中》にはどんな気持ちが動いていたのかな？ いったい何を難しいと感じたんだろうね？」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 440本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方／すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加（2020年11月13日）
この記事は『数学ガールの秘密ノート／図形の証明』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ！
![[icon]](https://img.hyuki.net/20220619121014-abd58cfc2ab436f4.png)