第310回 シーズン31 エピソード10

読むための対話：理由を求める問いかけ（後編）

平行線の錯角

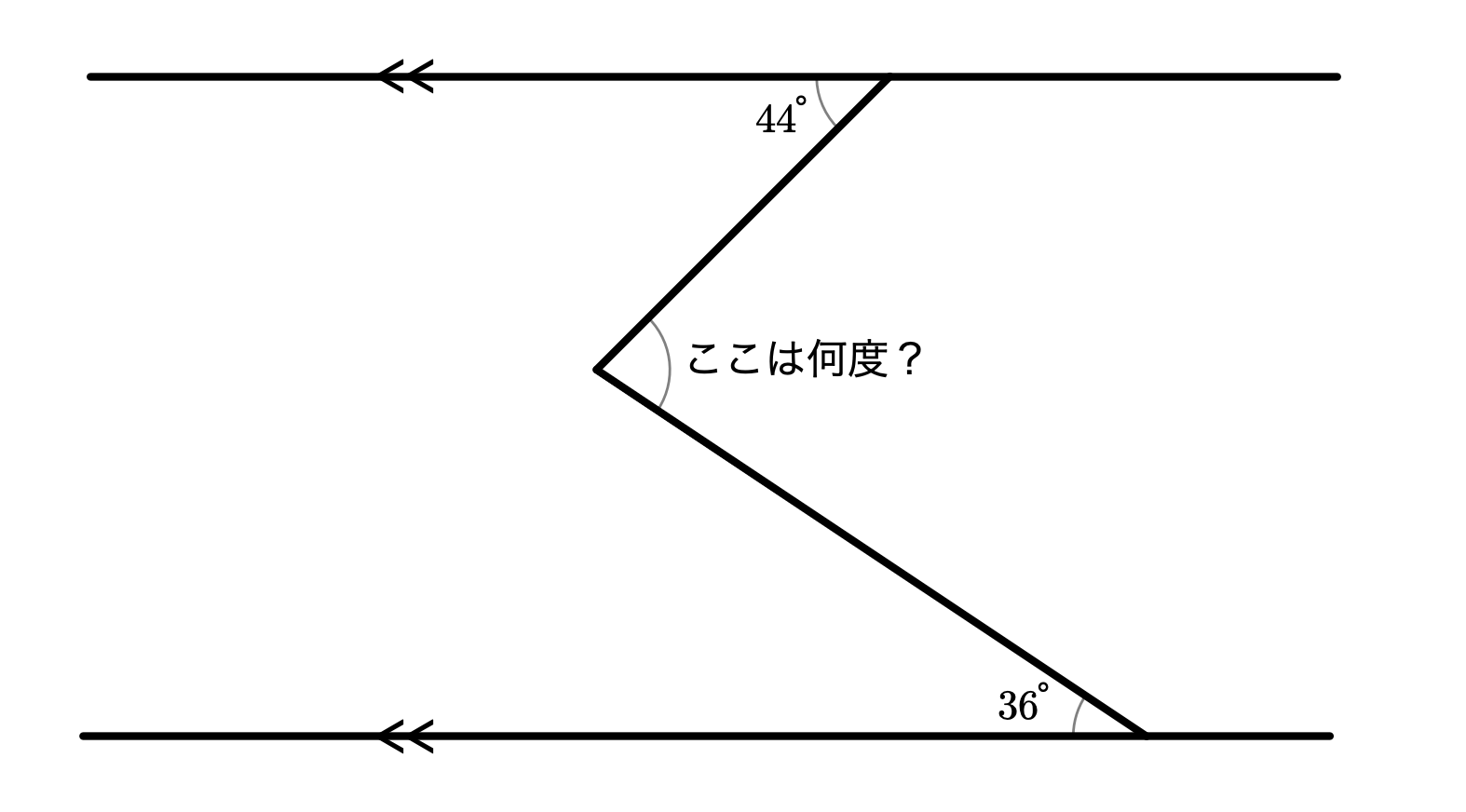
ノナ「補助線は……こうです $\NONA$」

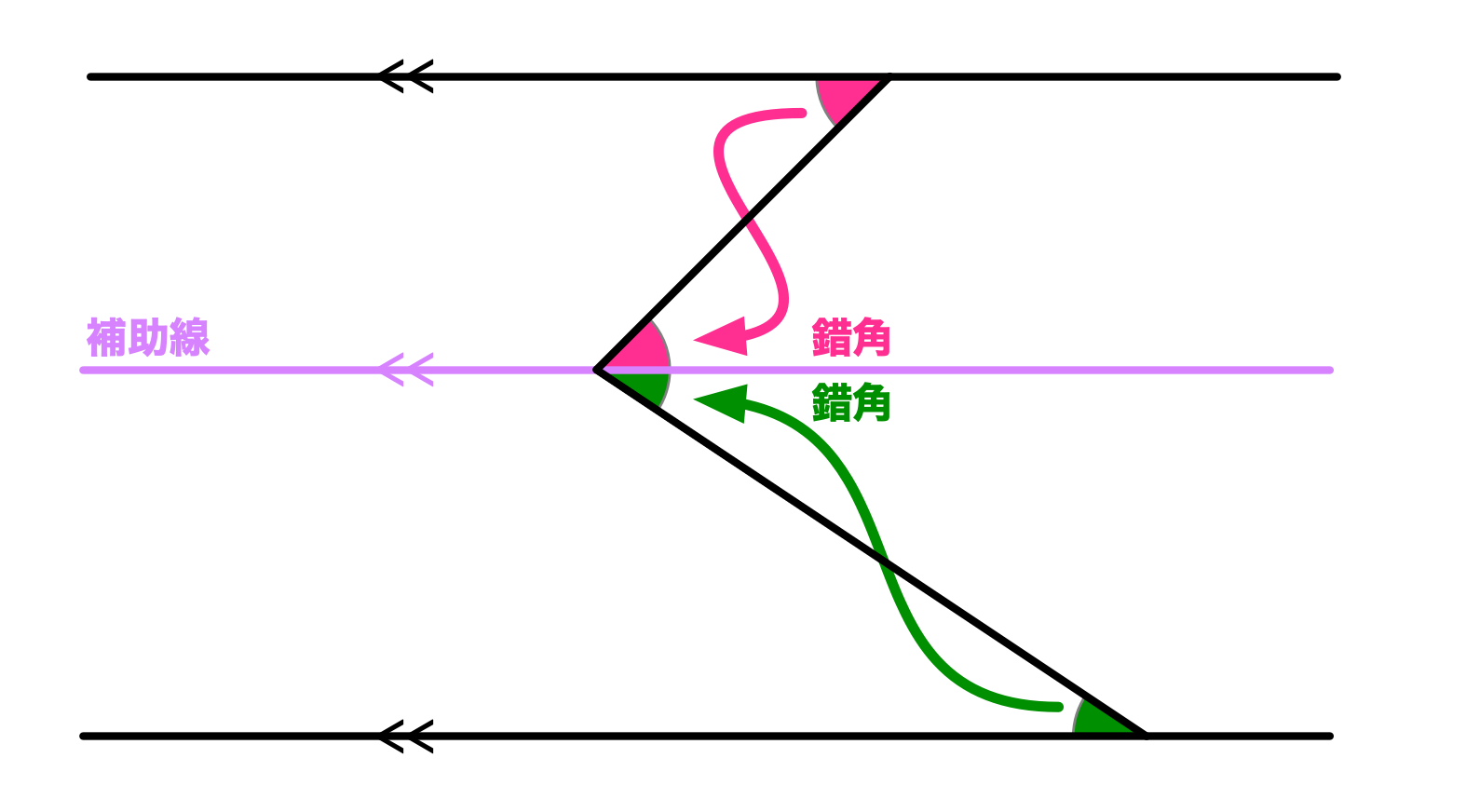
ユーリ「お兄ちゃんは、この補助線を引けなかったの？」

僕「そうだね。小学生で初めてこの問題を見たとき、この補助線を教えてもらって本当に驚いたよ。 この補助線があれば、《平行線の錯角は等しい》ということを使って、すぐに答えがわかる」

ユーリ「44度と36度を足して、80度」

ノナ「角を集める $\NONA$」

僕「そうだね。ノナちゃんの言う通り。《平行線の錯角は等しい》ということを使って角を一箇所に集める。 そうすれば、求める角の大きさがわかる」

ユーリ「《平行線の錯角は等しい》って、三角形の内角の和が180度であるのを証明するときも使ったよね（第309回参照）」

ノナ「$\NONA$」

僕「うん。そうだね。平行線の錯角が等しいことはよく使う」

ノナ「$\NONA$」

ユーリ「ノナ、どしたん？　あ……」

僕「気になることがあったら、何でも言っていいんだよ、ノナちゃん」

ノナ「理由は大事 $\NONAQ$」

僕「うん、そうだね。数学で理由は大事だよ。だから、理由がわからないことがあったら、どんなことでも聞いていいんだ。 どんなことでも『どうして？』と聞いていいからね」

ノナ「《平行線の錯角は等しい》は……どうしてですか $\NONAQ$」

理由を尋ねる

僕「なるほど！　《平行線の錯角は等しい》という主張の理由が気になったの？」

ユーリ「平行線の錯角が等しいのに理由ってあるの？　あるか……」

僕「理由というとわかりにくいかもしれないけれど、 《平行線の錯角は等しい》という主張を、 もっと基本的なことを使って証明することはできるよ。 ちょうど、さっきユーリが《三角形の内角の和は180度である》を証明したようにね（第309回参照）」

ユーリ「へー……」

僕「それにしても、ノナちゃんはすごいよ。本当にすごい」

ノナ「$\NONAQ$」

僕「『《平行線の錯角は等しい》のはどうして？』と、理由をきちんと聞いたよね。それはすごいことだよ」

ノナ「わからなかったの $\NONA$」

僕「そこがすごいんだ。みんなが当たり前だと思って話していることについて、 自分がわからないときに『それはどうして？』と質問するのには大きな勇気が要るよね。 すごく大きな勇気が要る」

ユーリ「ユーリもよく質問するよ！　『なんで？』って」

僕「そうだね。ユーリもよく理由を尋ねるよね。ユーリも偉いな！」

ユーリ「ふふん。だって理由がわかんないと、つまんないし。話を聞くだけになっちゃうから」

僕「そういうことだね。理由を尋ねるのは、自分で考えている証拠だ」

ノナ「何でも質問していい $\NONAQ$」

僕「もちろんだよ。だって、せっかくいっしょにおしゃべりしているんだから、質問したいときに質問しなくちゃ」

ユーリ「本読んでると、いらいらすることある。『え！　なんでそーなるの』と思っても質問できないもん」

僕「ああ、あるよね。考えながら本を読んでいると、理由を確かめたくなるから」

ユーリ「理由をちゃんと書いといてくれればいーのに」

ノナ「$\NONA$」

ユーリ「えーと、そんで、平行線の錯角が等しいことの証明は？」

僕「うん、たぶんできると思うんだけど、 いきなり証明を書くことはできないから、考えながら行きたいな。 考えやすいように問題の形にしよう」

問題1：平行線の錯角は等しいことを証明せよ

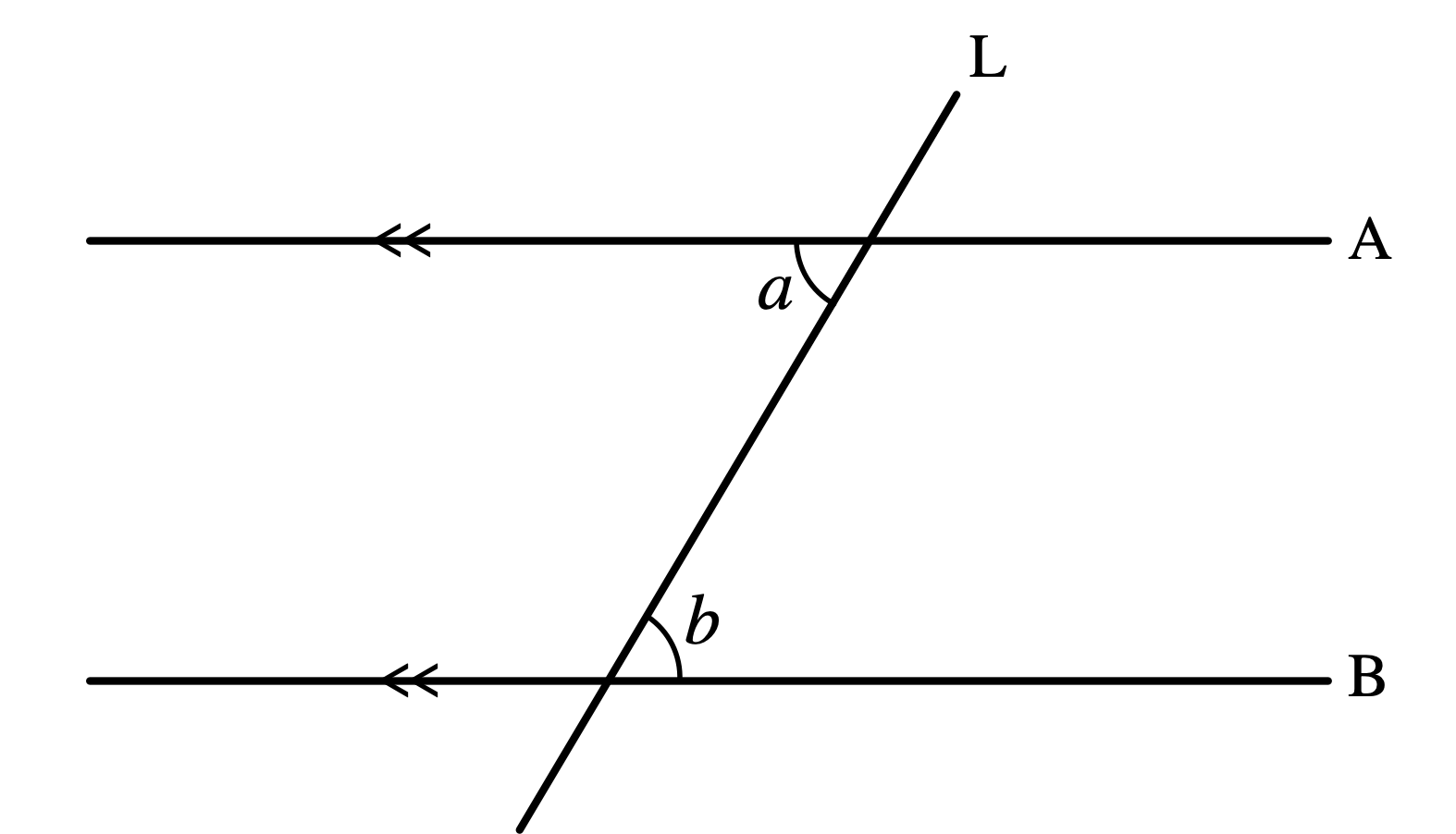
ユーリ「えー、こんなのどー考えるんだろ」

ノナ「結論 $\NONAQ$」

僕「ノナちゃんがいいことを言ったね。証明を考えるときには、まず、最後に示さなくてはいけない結論が何かをはっきりと押さえておこう」

ユーリ「$a = b$」

僕「うん、そうだね。結論は《角aと角bの大きさが等しい》ということだから、 aとbをそれぞれ角の大きさを表すものとするなら、 $$ a = b $$ が結論になる」

ユーリ「あとは仮定も？」

僕「そうなるね！　証明では、与えられた仮定も押さえておく必要がある。 仮定から結論までを理由の連鎖で繋がなくちゃいけないんだから。仮定は何だろう」

ノナ「平行 $\NONAQ$」

僕「そうそう。《直線Aと直線Bは平行である》というのが仮定。 二直線AとBが等しいことは、 $$ \PARALINES{A}{B} $$ と表すこともある。これが仮定。だから、すごく大ざっぱに書けば、証明はこんな感じになるんだろう」

ユーリ「大ざっぱ過ぎね？」

僕「いやいや、まあまあ。ここから自然と《AとBが平行であるならば、何がいえるだろう》と考えられるよね。 つまり、《AとBが平行である》ことからいえる次の一歩は何だろうか、と考えを進めるんだ」

ユーリ「《AとBが平行である》から、いきなり《錯角が等しい》に一歩で行っちゃダメだよね？」

僕「そりゃそうだね」

ノナ「《同位角が等しい》も……ダメですか $\NONAQ$」

僕「うん、僕もいまそれを考えていた。 《AとBが平行である》から《同位角が等しい》に進んで、さらに《対頂角は等しい》ことを使って《錯角が等しい》と進むことはできる。 それは、こんな証明になる」

ユーリ「証明はできたけど……」

僕「これでも一応、平行線の錯角が等しい証明にはなっている。 でも、この証明だと、新たな質問が出てくることになる。ユーリはわかるよね」

ユーリ「わかる」

僕「新たな質問、ノナちゃんはわかる？」

僕「この解答1aを読んで、ノナちゃんは何か気になる？」

ノナ「《平行線の同位角は等しい》のは……どうして $\NONAQ$」

僕「その通り！　いまの質問で、ノナちゃんが僕たちといっしょに考えているのがよくわかるよ！」

ノナ「わからなかったの $\NONA$」

僕「解答1aでは《平行線の錯角は等しい》の証明に《平行線の同位角は等しい》ということを使った。 これで《平行線の錯角は等しい》から《平行線の同位角は等しい》に問題が移ったことになる。 だから、《平行線の同位角は等しい》を証明しなくちゃいけなくなる」

ユーリ「同位角が等しいって証明するのに、錯角が等しいことを使っちゃダメだよね？」

僕「そうだね。循環論法（じゅんかんろんぽう）になってしまうから。これは論点先取と同じ種類のまちがいだ」

ユーリ「《対頂角は等しい》の証明も必要だし」

僕「確かに！　それもあるね……あ、でも対頂角が等しいことの証明はすぐできるけどね」

ユーリ「ふーん……《平行線の同位角は等しい》を使わないでも、問題1の証明ってできるの？」

僕「うん、それを考えてみようか」

ユーリ「考えてみようっていっても……」

僕「問題1の仮定は《二直線AとBは平行》だった。 だから、僕たちはここで、二直線が平行であることを定義しなくちゃまずい」

平行の定義

ユーリ「ほほー……平行の定義とな」

僕「うん。こんなふうに定義してみよう」

ユーリ「ふむふむ」

ノナ「はい $\NONA$」

僕「それから、平行に関しては《平行線の公理》が決定的に重要になる」

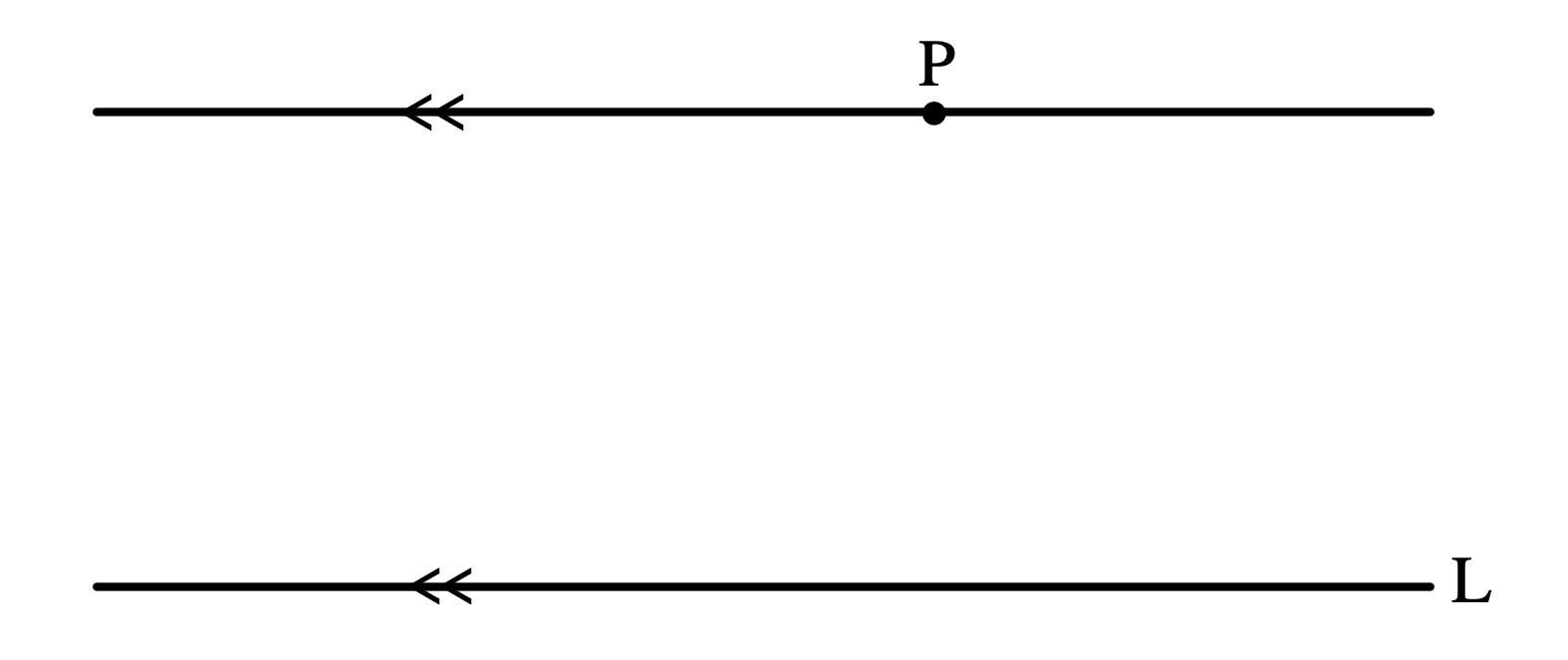
ユーリ「へー……これがそんなに重要なの？　 点Pは直線L上にないんだよね？　だったら、点Pを通る平行線が存在するって、当たり前じゃないの？」

僕「うん、これは数学の歴史上、めちゃめちゃ重要な意味を持っているんだ。 でもいまは、この《平行線の公理》を成り立つと認めることにする」

ユーリ「ふーん」

ノナ「ぽあんかれ……よそう $\NONA$」

僕「《平行線の公理》では、点Pを通る平行線が《存在する》というだけじゃなくて、《一本だけ存在する》というのが重要だからね」

ユーリ「それも当たり前じゃないの？　だって点Pを通る平行線が二本あったら……どっちかは直線Lにぶつかるに決まってるじゃん？」

僕「うん、それはユーリが《平行線というもの》を頭に思い描いているからだよね。 平行線というものはこういうものだというイメージが先にある。 そのイメージにしたがえば、平行線が一本だけ存在するのは当然だろう……という流れで考えている」

ユーリ「まーね」

僕「でも、この《平行線の公理》は、そういうふうに受け止めちゃいけないんだよ」

ユーリ「？」

僕「思い描く平行線のイメージを使って平行線についての何かを導くんじゃないんだ。 そうじゃなくて、平行線とは、この《平行線の公理》を満たしているものだと考えてほしい、ということ」

ユーリ「んんん？」

僕「平行線に関して何かを言いたかったら、この《平行線の公理》をおおもとの理由にしてね、ということ」

ユーリ「んー……」

ノナ「ダメなの $\NONAQ$」

僕「はい？」

ノナ「《平行線の公理》がどうしてなのか……質問してはダメですか $\NONAQ$」

僕「『《平行線の公理》がどうして成り立つんですか』という質問するのはもちろん構わないよ。 数学ではどんなことでも質問して構わないからね。 こんなことを質問してはダメかどうかなんて、まったく心配しなくていいんだよ、ノナちゃん。 数学では、何を質問しても馬鹿にされたり、怒られたりすることはないんだ」

ノナ「よかった $\NONA$」

僕「《平行線の公理》が成り立つ理由は、答えるのが難しいけれど、こうなるよ。 《平行線の公理》が成り立つということを前提にして、これからの議論を考えることにしよう、と定めたから。 それが理由だね」

ノナ「$\NONAQ$」

僕「公理というのは、定義と少し似ているところがある。 それ以上さかのぼって理由を考えなくてもいいことにしよう。ここを出発点として議論を展開しよう。 公理はそういう種類の主張なんだよ」

ノナ「難しい $\NONA$」

僕「数学のいろんな主張は、証明されてはじめて成り立つといえる。 でも証明で理由をどんどんさかのぼっていくと、どこまでいってもスタート地点が決まらない。 どこまで行っても『それが成り立つと言えるのはどうして？』と質問できるから」

ノナ「理由は大事 $\NONA$」

僕「そうだね。さかのぼっていくとやがて《直線AとBは平行である》のような主張にたどり着く。 でも、じゃあ、平行だとしたら何がいえるの？　となったときにどうすればいいか。 そのときに《平行線の公理》を使うんだ。 平行線については《平行線の公理》が成り立つものと決めておく。 そして、そこから何がいえるかを考える」

ユーリ「ちょーっと待った。《平行線の公理》は、ルールをそう決めたってこと？」

僕「そう考えていいよ。僕たちがふだん学校で習っているユークリッド幾何学では、《平行線の公理》がルールの中に含まれている。 それは決めごとだから、《平行線の公理》が成り立たないというルールにしてもいい。 別のルールを使うことに決めたならば、ユークリッド幾何学とは違う別の幾何学が生まれる」

ノナ「$\NONAEX$」

僕「それはまたものすごく楽しい話になるんだけど……話を戻そうか」

ユーリ「何考えてたんだっけ」

僕「ええと……そうそう、《平行線の錯角は等しい》ことを証明するんだった」

ユーリ「同位角を使わずに」

改めて、問題1：平行線の錯角は等しいことを証明せよ