第306回 シーズン31 エピソード6

読むための対話：「当たり前」を越えるため（後編）

二等辺三角形の証明問題

僕「じゃあ、ここまでに話してきたことをもとに、この問題を整理していくよ」

• 僕たちは「二等辺三角形は、二つの底角の大きさが等しい」ということを証明したい。
• 何が仮定で、何が結論かをはっきりさせたい。
• そのために三角形の頂点に名前をつけて、辺や角をはっきりさせたい。
• ノナちゃんの提案を使って、こんなふうに名前をつけて、問題を解きほぐしてみよう……

ユーリ「確かにそーだけど、くどいにゃあ」

ノナ「これが証明 $\NONAQ$」

僕「いやいや、これはまだ証明じゃないよ、ノナちゃん。 これは、与えられた問題を考えていくために、解きほぐしてみただけ。 ノナちゃんが提案してくれた《三角形ABCと名前をつける方法》を使って、 問題を言い換えたんだ。これで……」

• 「二等辺三角形である」という仮定は、「$\TT{AB} = \TT{AC}$ である」とはっきり表せる。
• 「底角が等しい」という結論は、「$\ANGLE{ABC} = \ANGLE{ACB}$ である」とはっきり表せる。

ノナ「はっきり……しました $\NONA$」

ユーリ「ノナ、元気ないじゃん。お腹減った？」

ノナ「証明はわからないけど……底角は等しいです。こことここ $\NONA$」

僕「そうだね。二等辺三角形を描けば底角が等しいことは確かに成り立ちそうだとわかるし、実際に底角は等しいよ。 でも、仮定はあくまで《二辺の長さが等しい》というだけだよね。 僕たちはそこから結論の《二等辺三角形の底角の大きさは等しい》まで、しっかりとつなげてやらなくちゃいけない」

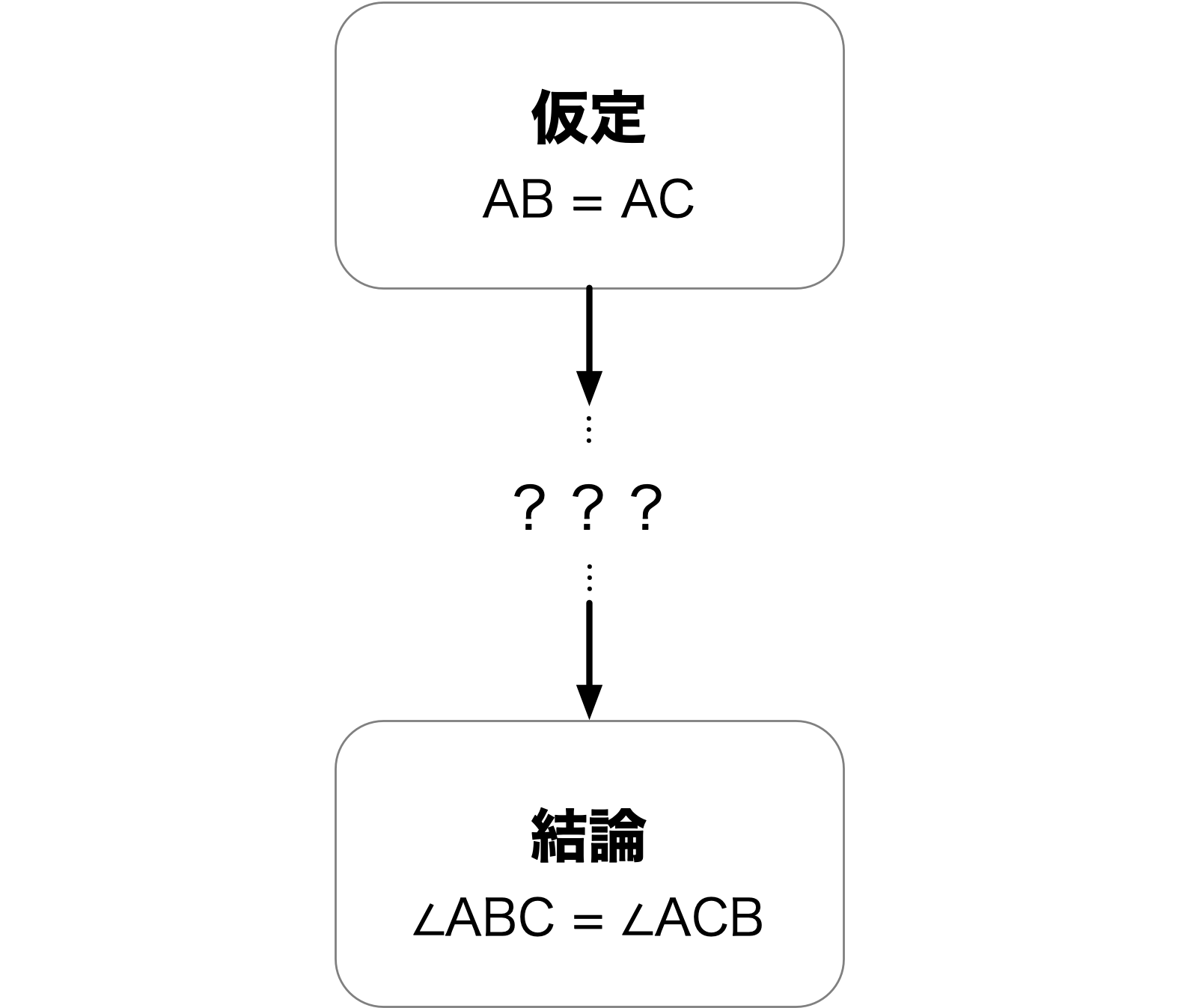
ノナ「あたりまえで……難しい $\NONA$」

僕「うん、そう感じるのはすごく自然だよ。事実として知っていることをわざわざ証明しなさいと言われたら『当たり前じゃないか』と言いたくなったり、 『当然でしょ』と言いたくなる。僕たちがやろうとしているのは、わかってしまえば確かに当たり前かもしれないけど、 仮定と結論をつないでやることなんだ。偉い人が言ったからでもなく、声が大きい人が言ったからでもなく『これこれこういう理由で成り立つ』と言いたい。 それが証明だから」

ノナ「理由が大事 $\NONAEX$」

僕「ところで、ユーリはもう証明は見つけたの？」

ユーリ「見つけたってゆーか、わかってるよん。学校で習ったんだっけかなー……」

ノナ「やってないよう……覚えてない $\NONA$」

僕「習ったかどうか、覚えているかどうかは、ちょっとわきに置いとこう。 どうしたら証明を見つけることができるか、そのヒントを考えてみるね。 もう僕たちは、 二等辺三角形や底角という言葉の意味はわかっているし、 この問題が全体として何を聞いているかもわかっている（第305回参照）。 それから、数式を利用して言いたいこともはっきりした。 仮定も結論もわかっている。 あとは、仮定から結論までをつなげればいい。そうだよね」

僕「こうすれば絶対に証明を見つけられる！なんて方法はないけれど、 証明を探すヒントとなる方法はたくさんある。 たとえば《仮定からスタートして、その仮定から言えることを探していく》方法があるよね。 それから逆の方法もある。つまり《結論からスタートして、何が言えたらその結論が言えるかを探していく》方法」

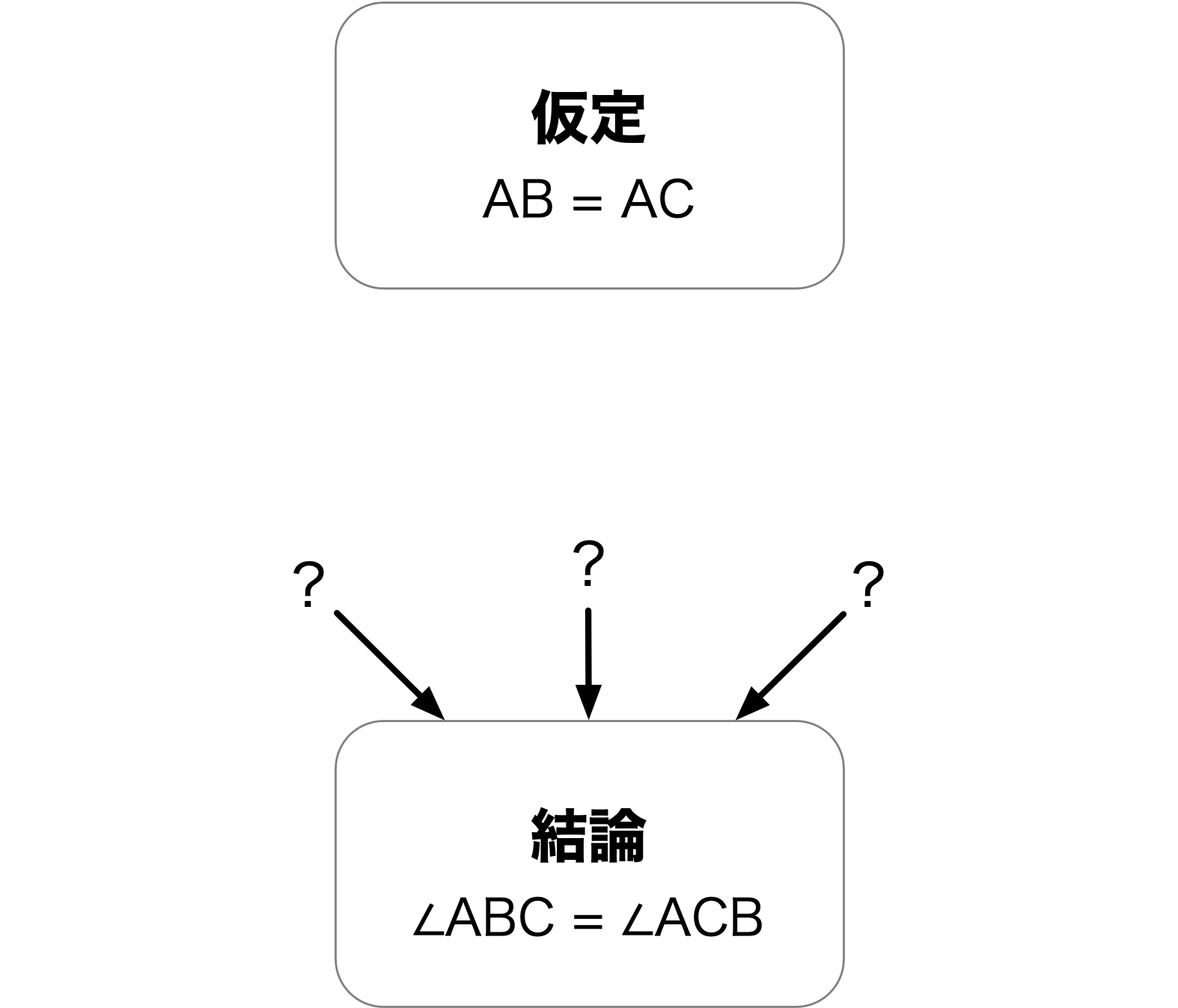
ユーリ「ユーリ、それ好き！　出口から逆に戻るんでしょ？」

僕「そうだね」

ユーリ「三角形が合同だと言えれば、 $\ANGLE{ABC} = \ANGLE{ACB}$ が言えるじゃん！」

僕「大きなヒントが出ちゃったな」

ユーリ「あっと、ごめーん！ 我慢してたんだけどなー」

ノナ「ヒント $\NONAQ$」

僕「ユーリが言ったのは、こういうことだよ。僕たちが証明したい結論は二つの角の大きさが等しいということ。 つまり、 $\ANGLE{ABC} = \ANGLE{ACB}$ を言いたいわけだよね」

ノナ「はい $\NONA$」

僕「そこで考えたいのは《何が言えたら、二つの角の大きさが等しいと言えるのかな》ということだね。 これは《似た問題を知らないか》という問いかけにもできるよ。 自分が知っていること、自分が覚えていることの中から《こういうときには二つの角の大きさが等しい》という知識を探してくることになる」

ノナ「暗記……暗記ですか $\NONA$」

僕「暗記といえば暗記かもしれないけど……少なくとも丸暗記ではないよ。 自分が覚えている知識の中から探してくるというのは確かだけどね。 たとえば、ノナちゃんは『これこれこういうとき、二つの角の大きさは等しくなります』という知識を持ってる？」

ノナ「合同な三角形……ですか $\NONAQ$」

ユーリ「ぴんぽーん！　正解！」

僕「そうそう！　合同な三角形はいいね！」

ノナ「当たりました $\NONAHEART$」

僕「当たったといっても悪くはないけど、これがたったひとつの正解ではないよ。《こういうときには二つの角の大きさが等しい》といえる場面は無数にあるから。 でも、合同な三角形を使うのはいい考えだね！」

ノナ「$\NONAHEART$」

僕「ところでノナちゃん。『合同な三角形』のように単語で答えるんじゃなくて、 『これこれこういうとき、二つの角の大きさは等しくなります』みたいに文章で答えることをやってみて」

ノナ「合同な二つの三角形だと……対応する角の大きさは等しい……等しくなります $\NONA$」

僕「すばらしい！」

ノナ「まちがいですか $\NONAQ$」

僕「いやいや、何もまちがいじゃないけど？」

ノナ「三角形は一つしかない……一つだけです $\NONA$」

僕「ああ、そうだね。僕たちの前には三角形は一つしかない。 三角形が一つしかないのに合同を考えるのが引っかかる？」

ノナ「$\NONA$」

僕「でも、ノナちゃんはさっき、左手と右手を動かして底角を確認していたよね。 それを続けて三角形を描けば、左手が描く《三角形ABC》と右手が描く《三角形ACB》という二つの三角形が生まれる」

ユーリ「こーゆーこと」

ノナ「それもアリなの……アリですか $\NONAQ$」

僕「うん、アリだよ。三角形ABCと三角形ACBについて、合同を考えてもかまわない。 だってどちらも三角形だからね。 これでアイディアは出そろったから、証明の形にしてみるよ」