![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/図形の証明』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ノナ:ユーリの同級生。 ベレー帽をかぶってて、丸い眼鏡を掛けていて、ひとふさだけの銀髪メッシュ。 数学は苦手だけど、興味を持ってる中学生。
僕「うん、じゃあ、別の問題に取り組んでみよう。ユーリもノナちゃんもまだ疲れてない?」
ユーリ「ぜんぜん」
ノナ「大丈夫……大丈夫です $\NONA$」
僕「さっきは三角形の証明問題だったけど(第304回参照)、今度も証明をする問題だよ」
問題
二等辺三角形は、二つの底角の大きさが等しい。このことを証明してください。
ユーリ「あー、これ知ってる!」
ノナ「ユーちゃん、待って $\NONA$」
ノナはそう言って、問題を読む。
僕は彼女の視線を追う。
視線の動きはゆっくりで、しかも何度も往復している。当然ながら、それなりに時間が掛かる。
ユーリは何かを言いたげに口を開いたり、また閉じたりしている。 いろいろと話したいことがあるんだろうけれど、よく我慢している。 ノナが考えるのを邪魔しないためだろう。
僕「……」
ユーリ「『ねえノナちゃん、ゆっくり考えていいからね。時間はたっぷりあるんだから』」
僕「ねえユーリ、それはもしかして僕のモノマネ?」
ユーリ「もちろん」
僕「そんな話し方してるかなあ」
ユーリ「してるしてる。ぴったり同じ」
ノナ「わかりません $\NONA$」
僕「ノナちゃんは、この問題が何を聞いているかはわかる?」
ノナ「『二等辺三角形は、二つの底角の大きさが等しい……このことを証明してください $\NONA$』」
僕「うん、ノナちゃんは問題文を正確に読んでくれたね。ぴったり同じ。 言葉としては問題をちゃんと読めている。問題の意味はどう? 問題の意味はノナちゃんに伝わっている?」
ノナ「$\NONAQ$」
僕「たとえば……うん、ユーリだったらノナちゃんに何て聞く?」
ユーリ「こっちに振るんかい! びっくりしたじゃん。えっと……『二等辺三角形って知ってる?』」
ノナ「わかってるよう $\NONA$」
ユーリ「『底角って知ってる?』」
ノナ「そっちも覚えてる $\NONA$」
ユーリ「だったら証明できるよ!」
僕「ありがとう、ユーリ。そうだね。ユーリが聞いてくれたみたいに『二等辺三角形』や『底角』という言葉について聞くのは大事。 問題に出てくる言葉の意味がわからなければ、問題の意味もわからないから」
ユーリ「ふふん。定義を聞くのは基本だもんね!」
僕「でもそこで『知ってるか』と聞いちゃうと、 知ってる、わかっている、覚えている……で話は終わっちゃう」
ユーリ「わかってるなら、それでいーのでは?」
僕「でも、本当にわかってるかどうかはまだはっきりしない。言葉として表されてないからね」
ノナ「外ですか $\NONAQ$」
僕「え? ああ、そうそう! 『どういう三角形を二等辺三角形というのか』という二等辺三角形の定義が、 ノナちゃんの中から外に言葉になってまだ出てきていない。 だから、『二等辺三角形の定義は何ですか』のように《定義を問う》ことが大事だね」
ノナ「知ってる……本当に知ってます $\NONA$」
僕「うん、ノナちゃんは二等辺三角形の定義を知っている。それを疑っているわけじゃないし、 ノナちゃんがウソをついてると非難しているわけでもない。 でも、数学で対話をするときにはいつも、ほんとうにいつも、《定義を問う》ことをお互いに行う」
ユーリ「やるやる。聞く聞く」
僕「一人で数学を考えるときもそうだよ。自分に対して《定義を問う》ことはとても多い。 自分に対して問う……つまり自問するんだ」
ユーリ「じもん」
ノナ「じもん $\NONA$」
僕「一人で考えているときは自分に対して『この言葉の定義は何か』と自問する。 話している相手がいるときは『なになにの定義は何ですか』や、『その言葉をどんな定義で使っていますか』や、『定義を教えてください』みたいに問うんだ。 数学では《定義を問う》ことはまったく失礼じゃないし、悪いことでもないんだよ。逆に、とても大切なこと」
ノナ「聞いてもいいの $\NONAQ$」
僕「うん、そうだよ。 だって、《定義を問う》というのは『あなたの話をしっかりと聞きますよ。ちゃんと聞きたいですよ』という気持ちの表れだからね」
ノナ「二辺の長さが……等しい三角形です $\NONA$」
僕「うん、それで正しい。二辺の長さが等しい三角形を二等辺三角形という。これは二等辺三角形の定義だね」
ユーリ「名前のまんまだ」
ノナ「$\NONAQ$」
僕「そうだね。『二等辺三角形』という名前の通り。『二つの等しい辺をもつ三角形』ということだからね」
ユーリ「ノナは『底角』の定義を知ってる? じゃなくて、底角の定義は何?」
ノナ「底角……わかりません $\NONA$」
ユーリ「知ってるはずじゃん」
ノナ「何て言えばいいかわかんない $\NONA$」
僕「ノナちゃんはときどき『わかりません』とだけ答えるときがあるけど、 いまユーリに言ったみたいに『何と言えばいいのか、わかりません』と答えた方がいいかもしれないよ」
ノナ「$\NONAQ$」
僕「『わかりません』だけだと、何にもわからないみたいに聞こえちゃうから。 ノナちゃんは底角の定義をパパッと言葉で外に出すことはできないかもしれないけど、 ノナちゃんの中にはわかっていることがあるんだよね?」
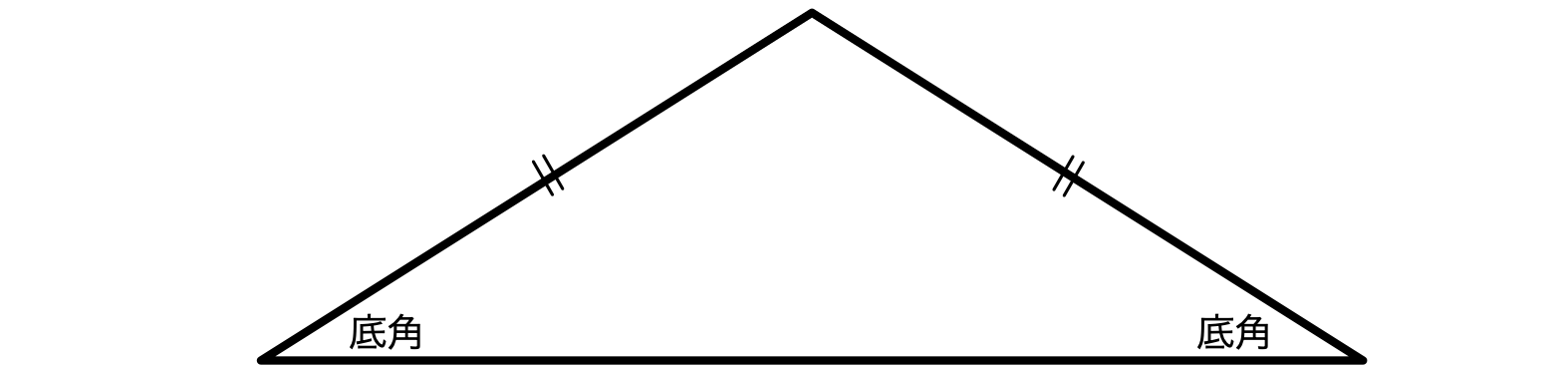
ノナはこくんとうなずいて、こんな図を描いた。
ノナ「底角はこれとこれです $\NONA$」
二等辺三角形と二つの底角
ユーリ「ほらー、ノナは知ってるじゃん!」
ノナ「わかってるもん $\NONA$」
僕「いま、ノナちゃんが図を描いたのはすごく大事なことだね。 ノナちゃんが、図を使って『底角はこれのこと』だと教えてくれたから『うん、ノナちゃんは確かに底角が何であるかわかっている』と僕にも伝わった。 たとえ、定義を言葉で表せなくても、そんなふうに何とかして伝えるのは大事だね」
ノナ「外に出す $\NONAQ$」
僕「そうそう! ノナちゃんは、自分の《中》にある理解を《外》に出してくれたんだ」
ユーリ「ところで、底角ってどーゆー定義? 言葉だと」
僕「ユーリだったらどんなふうに言う?」
ユーリ「いやー、結構むずいね」
僕「そうなんだよ。実際にやろうとすると難しい。だから、やってみるのは大事だね。 たとえばこんなふうに」
二等辺三角形の頂角と底角
二等辺三角形には、長さが等しい二つの辺があります。
その二つの辺が作る角を、その二等辺三角形の頂角(ちょうかく)といいます。
二等辺三角形が持つ三つの角のうち、頂角以外の二つの角を、その二等辺三角形の底角といいます。

ユーリ「あっ、それズルくない? 《頂角以外の角》で定義すんの?」
僕「いやいや、こういうのはズルいとは言わないよ。だって、はっきりするだろう? それに、底角だけじゃなくて頂角も定義しておけば便利だし」
ユーリ「むー……」
ユーリは腕組みをして真剣に考え始めた。
何を考えてるんだ?
ノナ「$\NONA$」
ユーリ「むー……こーゆーのは?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2020年10月16日)
この記事は『数学ガールの秘密ノート/図形の証明』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!