第302回 シーズン31 エピソード2

読むための対話：三角形の重ね合わせ（後編）

三角形の合同

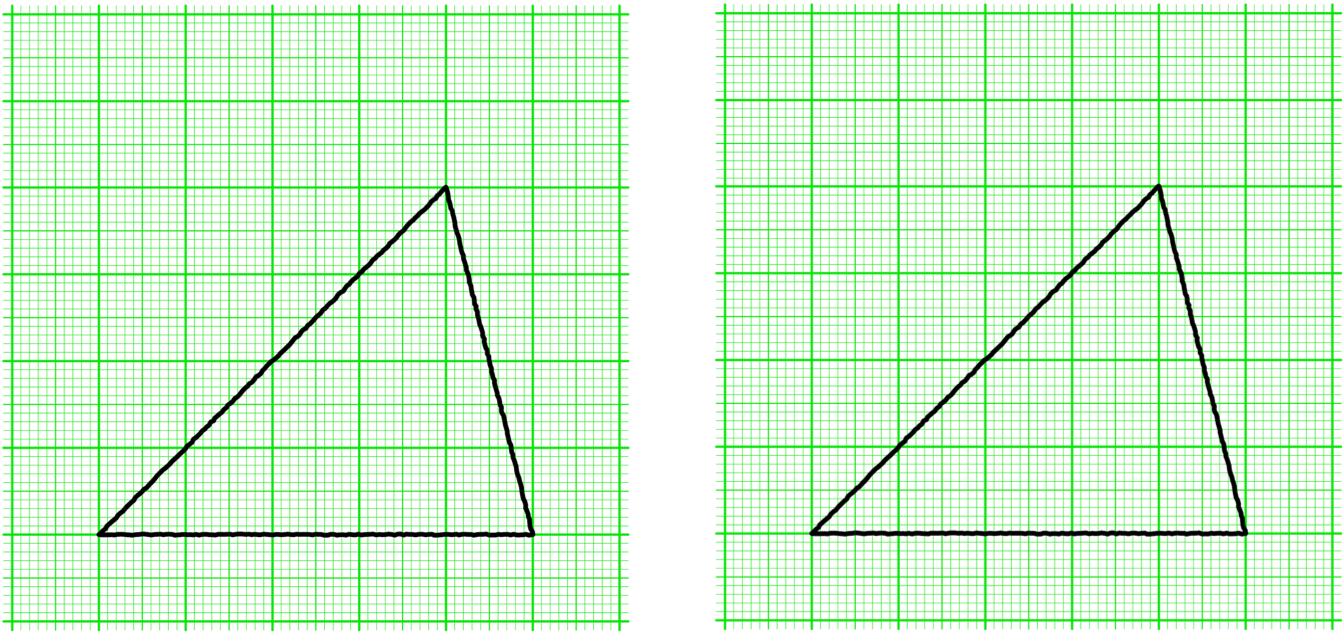
僕「……二つの三角形をぴったりと重ねることができるとき、その二つの三角形は合同であるという。 ところで、三角形には三つの辺と、三つの角がある。 二つの三角形をぴったりと重ねると、辺と辺、角と角もまた、ぴったりと重なることになる」

ユーリ「ちょっと待った。その説明ひどくない？」

僕「『地の文にまでツッコむユーリであった』」

ユーリ「ったくもー！」

僕「一つの三角形に辺は三つあるし、角も三つある。三角形が二つになったら、辺も角も個数が倍になる。 たくさんあるとややこしくなるし、まちがいやすくなる。 数学では、いろんなものごとをはっきりさせて話を進めたい。 じゃあ、どうすればいいと思う？」

ノナ「$\NONAQ$」

ユーリ「そんなの、簡単！　名前を付ければいーじゃん！」

僕「そうだね。三角形の辺や角に名前を付ければいい。 そうすればまちがいは少なくなる」

ノナ「わからない……わかりません $\NONA$」

三角形の頂点

僕「うん、何にも難しい話じゃないよ。三角形には三つの頂点（ちょうてん）がある。 そこに、たとえば $A,B,C$ のように名前を付けるんだ」

ユーリ「ちょうてん」

ノナ「ちょうてん $\NONA$」

僕「そうだね。自分で名前を付けるときには、好きな名前を付けて構わない。 $A,B,C$ でもいいし、 $D,E,F$ でもいい。どんな名前でもいい」

ユーリ「《ぜぁずのっぷれっすらいっほんむ》でもいい」

僕「There's no place like home...そんなに長い名前は普通は付けないよ、ユーリ」

ユーリ「どんな名前でもいいってゆった」

僕「うん、確かにそう言ったし、付けたかったらThere-is-no-place-like-homeなんて名前を頂点に付けてもいい。 でもそれは長すぎて不便だから、たいていはアルファベット一文字を使うね。書くときは大文字にすることが多い。 そうでなければいけないってわけじゃないけれど」

ノナ「$\NONA$」

三角形の名前

僕「ともかく頂点三つに名前を付けた。これで、この三角形を『三角形 $ABC$』と呼ぶことができる。 $ABC$ は、三つの頂点 $A,B,C$ の名前を続けただけだよ。 点に名前が付いていて、その名前を呼べばどの点のことをいってるかはっきりとわかるから、 『三角形 $ABC$』と呼ぶだけで、どの三角形のことかよくわかる」

ユーリ「『三角形 $BCA$』とか『三角形 $ACB$』でもいーんでしょ？」

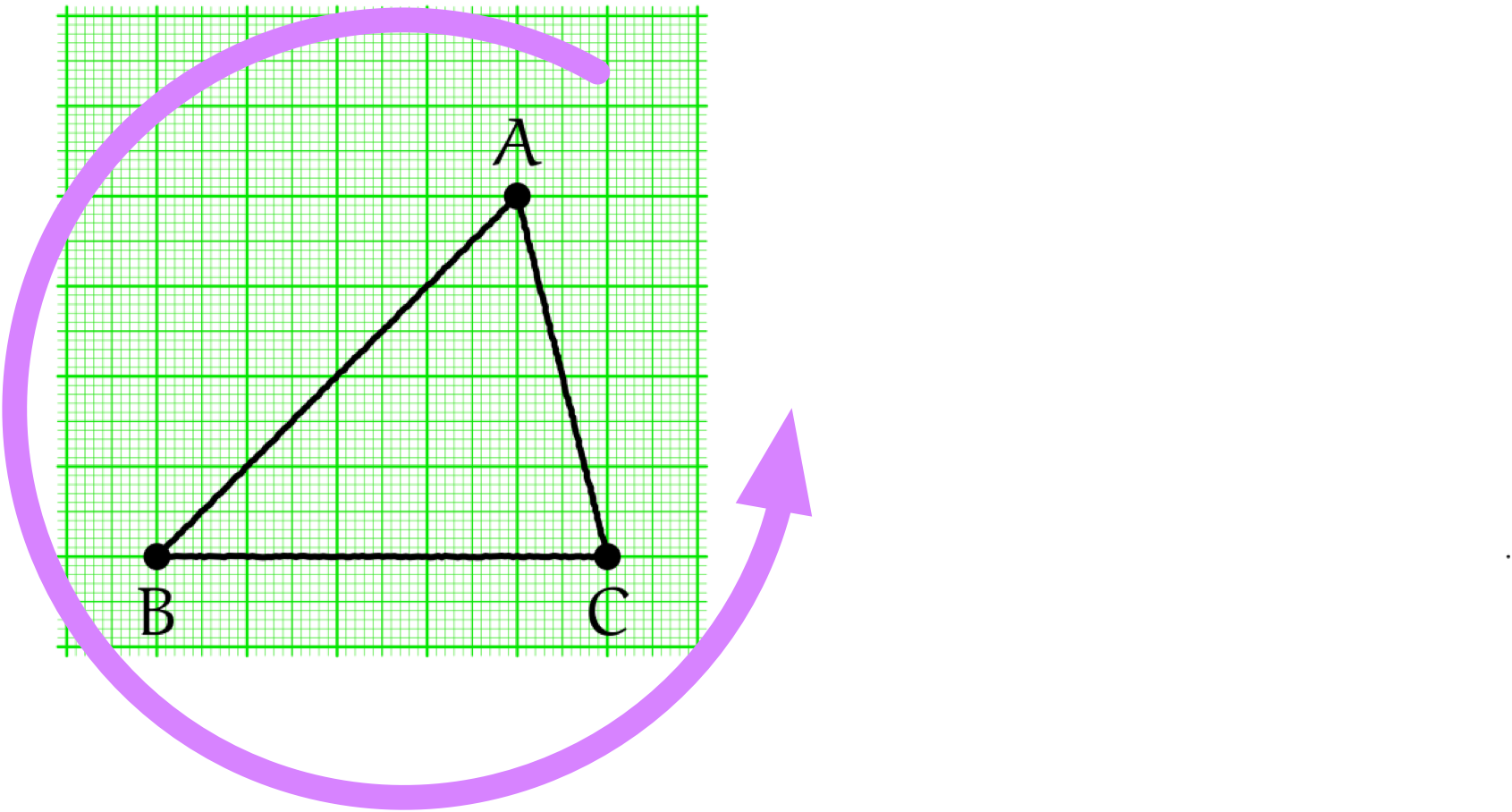
僕「そうだね。それはとても大事な話。三角形の頂点を並べる順番は基本的にはどうでもいいんだけど、 たいていは反時計回り、つまり時計の針が動く向きとは反対の向きに呼ぶことが多いね」

ユーリ「ふーん」

ノナ「同じなの……同じですか $\NONAQ$」

僕「同じって、何が？」

ノナ「頂点と点は、同じですか $\NONAQ$」

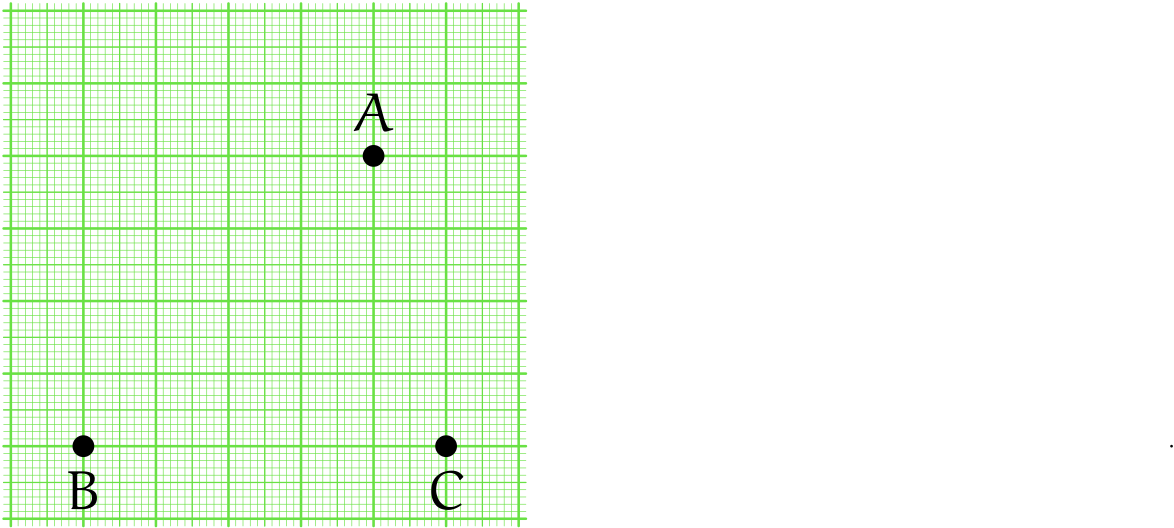
僕「え、ああ……もしかして、頂点と点を両方混ぜこぜにしてた？ うん、三角形 $ABC$ を使って説明するよ。点 $A$ と、点 $B$ と、点 $C$ という三つの点がある。これらはもちろん点だね」

僕「そして三角形 $ABC$ を描く。 この点 $A$ と点 $B$ と点 $C$ という三つの点のことを、この三角形の頂点と呼ぶ。 だから、頂点はどれも点だよ。 でも、点は三角形の頂点とは限らない。 たとえば、点 $D$ や点 $E$ や点 $F$ をこんなふうに描いたとすると、 点 $D$ も点 $E$ も点 $F$ も、三角形 $ABC$ の頂点ではない」

ユーリ「でもさー、三角形 $DEF$ を描いたら、点 $D$ や点 $E$ や点 $F$ も頂点だよね？」

僕「もちろんそうだね。点 $D,E,F$ は三角形 $DEF$ の頂点といえる」

ノナ「わかる……わかりました $\NONA$」

僕「それにしても、ノナちゃんはすごいよ！」

ノナ「$\NONAQ$」

僕「『頂点と点が同じか』という疑問を持ったことだよ！　それは言葉を注意深く聞いていないと気付かない。 数学は、言葉を大切にする。だから、言葉を注意深く聞いたり、注意深く使うことはとてもいいことなんだ」

ユーリ「ねーねー、ノナが質問したのもすごくね？　ユーリより先にお兄ちゃんにツッコミ入れたんだよ？」

僕「もちろん、そうだね！」

ノナ「$\NONA$」

三角形の辺

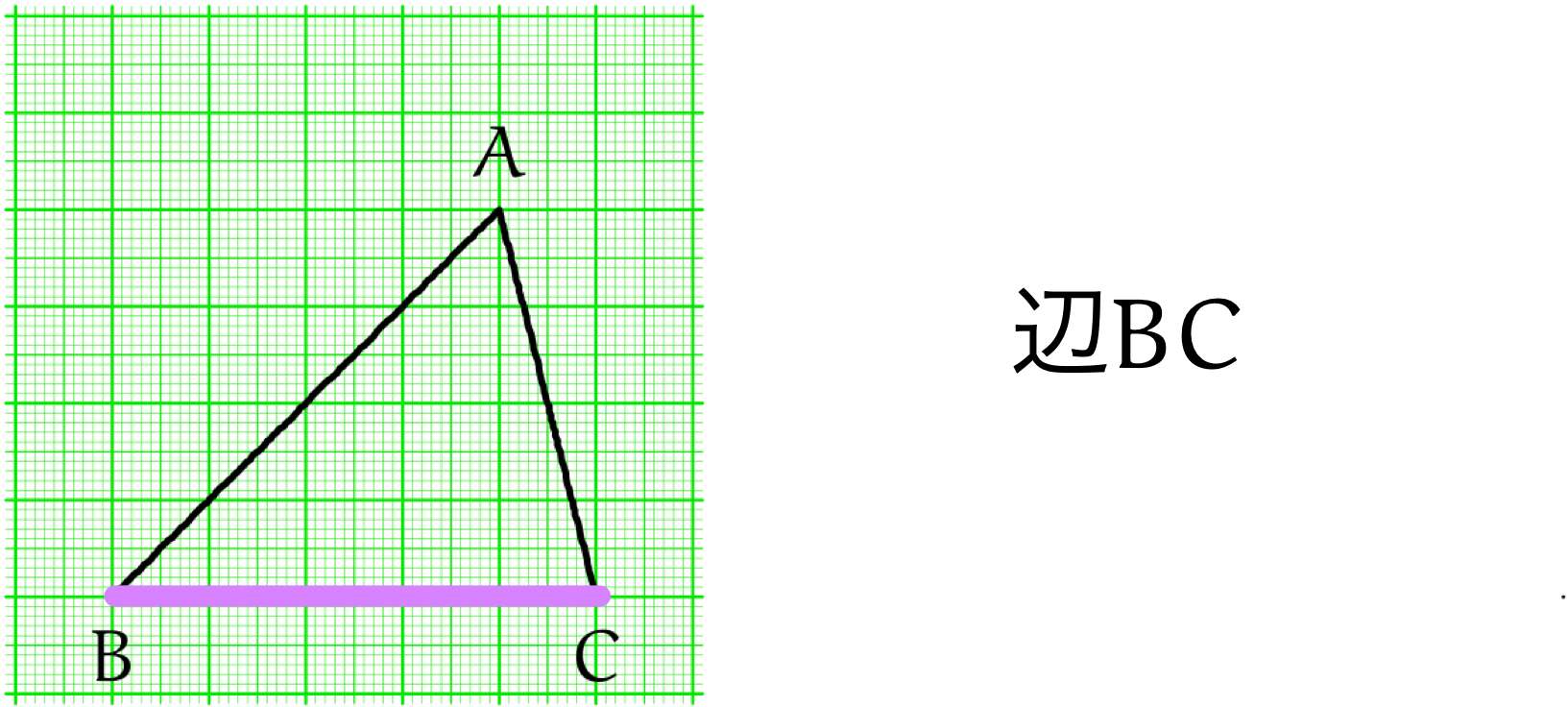
僕「じゃあ、話を続けようか。三角形 $ABC$ には三つの辺がある。 頂点に $A,B,C$ という名前が付いたから、辺の両端にある点の名前を使えば、辺を呼ぶことができる。 つまり、辺 $AB$ と、辺 $BC$ と、辺 $CA$ のように呼ぶことができる」

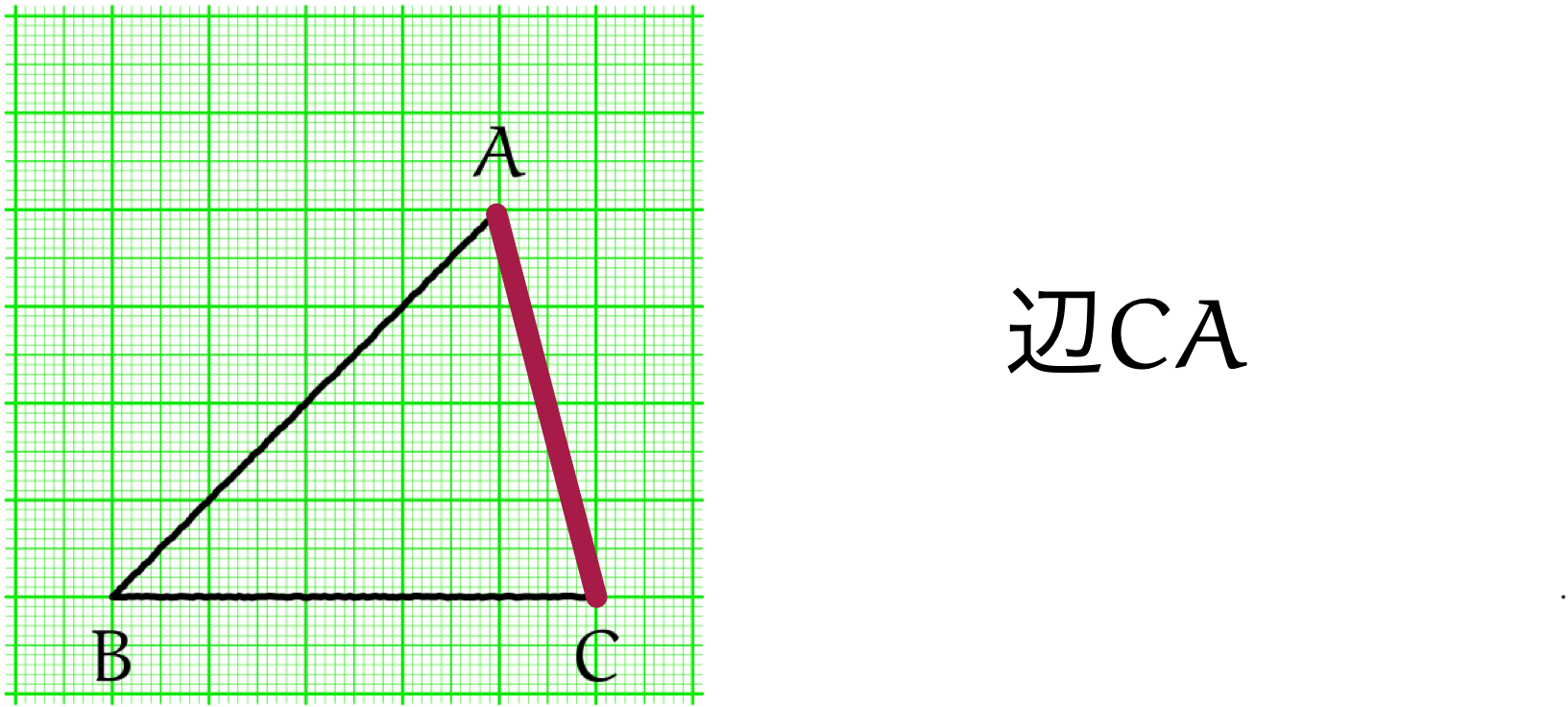
ユーリ「辺 $CA$ って、辺 $AC$ じゃないの？」

僕「うん。いまは辺 $AC$ でも、辺 $CA$ でもどちらでもいいよ。どちらも同じ辺を指していることがはっきりわかるからね」

ユーリ「なんで『いまは』なの？　どちらでもよくないときもあんの？」

僕「そうだね。頂点の順番をはっきりさせた方がいいときがあるから……うん、そうだ。大事なことを話そう。 『そういう名前がいいかどうか、どうすればわかるか』の話だよ」

ユーリ「何言ってるかわかんない」

どんな名前がいいのか

僕「点に名前を付けることにも、三角形や辺に名前を付けることにも、どんなことにも当てはまるんだけど、 名前を付けるのは、どれのことを指しているかをはっきりさせるためなんだよ。はっきりさせるのが名前を付ける目的」

ユーリ「んー、それは当たり前の話では」

僕「そうそう、当たり前の話だよ。でも、大事な話。 数学では、頂点や、頂点以外の点や、辺や、角や、三角形や……たくさんのものが出てくる。 だから、うっかりすると何の話をしているのか、どれのことを指しているのか、ごちゃごちゃしちゃう」

僕「ごちゃごちゃしては、数学はできない。そこで、名前を付ける。名前を付けるのは、どれのことを指しているかをはっきりさせるため。 だから、三角形 $ABC$ とか、辺 $AB$ のような名前がいいかどうかは、どれのことを指しているかがはっきりしたかどうかでわかる」

ユーリ「ほほー」

僕「もしもその名前で『なるほど、これのことだな』とはっきりするなら、良い名前だね。 でも、『結局、どれのことかわからない』となったら、悪い名前だ」

ノナ「先生じゃない $\NONAEX$」

僕「え？」

ユーリ「ノナ、どしたん？」

ノナ「先生じゃなくて……自分ですか $\NONAQ$」

僕「ええと……ごめん、もう少し話して？」

ノナ「先生が言ったからじゃない……《理由》が大事なんです $\NONA$」

僕「うん、そうだね。先生が言ったから正しいんじゃなくて、ちゃんと《理由》があるから正しいんだよ。 もちろん、先生が言ったから間違いというわけでもないから注意してね。 大切なのは《理由》を考えること。三角形 $ABC$ と呼べば、どの三角形かはっきりする。はっきりすれば、話が混乱しない。 そういう理由があるから、三角形 $ABC$ という言い方をしているんだ。 『どっちでもいいけど、多くの人がそう書いているからそれに合わせましょう』という理由のときもある」

ユーリ「$\TRIANGLE{}ABC$ って書くときもあるよね。これは？」

僕「ユーリは、どう思う？」

ユーリ「いちいち『サンカッケイ』って書くより楽。めんどくさくない」

僕「そうだね。何を言ってるかはっきりするし、すぐに書ける。だから、良い方法だね」