![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png)
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート／図形の証明』として書籍化されています。
登場人物紹介
僕：数学が好きな高校生。
ユーリ：僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ノナ：ユーリの同級生。 ベレー帽をかぶってて、丸い眼鏡を掛けていて、ひとふさだけの銀髪メッシュ。 数学は苦手だけど、興味を持ってる中学生。
僕「合同な二つの三角形があったとする。 では、その二つの三角形についてどんなことが言えるだろうか。 二つの三角形が合同ならば、ぴったりと重ねることができる。 だから、三組の辺の長さはそれぞれ等しくなるし、三組の角の大きさもそれぞれ等しくなるよね」
僕は改めて話し出す。
僕とユーリとノナ。 僕たちの数学トークは、 ちっとも前に進まず、その場で《足踏み》しているみたいだ。
三角形の合同とは何か。頂点や辺や角に名前をつけるということ。名前と図の対応を確認すること……そこまでたどりつくだけでどれだけ時間が過ぎただろう（第302回参照）。
でも、たくさん《足踏み》したから、足場がそれだけ固まったようにも感じる。
ユーリ「どんどんいこー！」
ノナ「行こう $\NONA$」
合同な二つの三角形、 $\TRI{ABC}$ と $\TRI{DEF}$
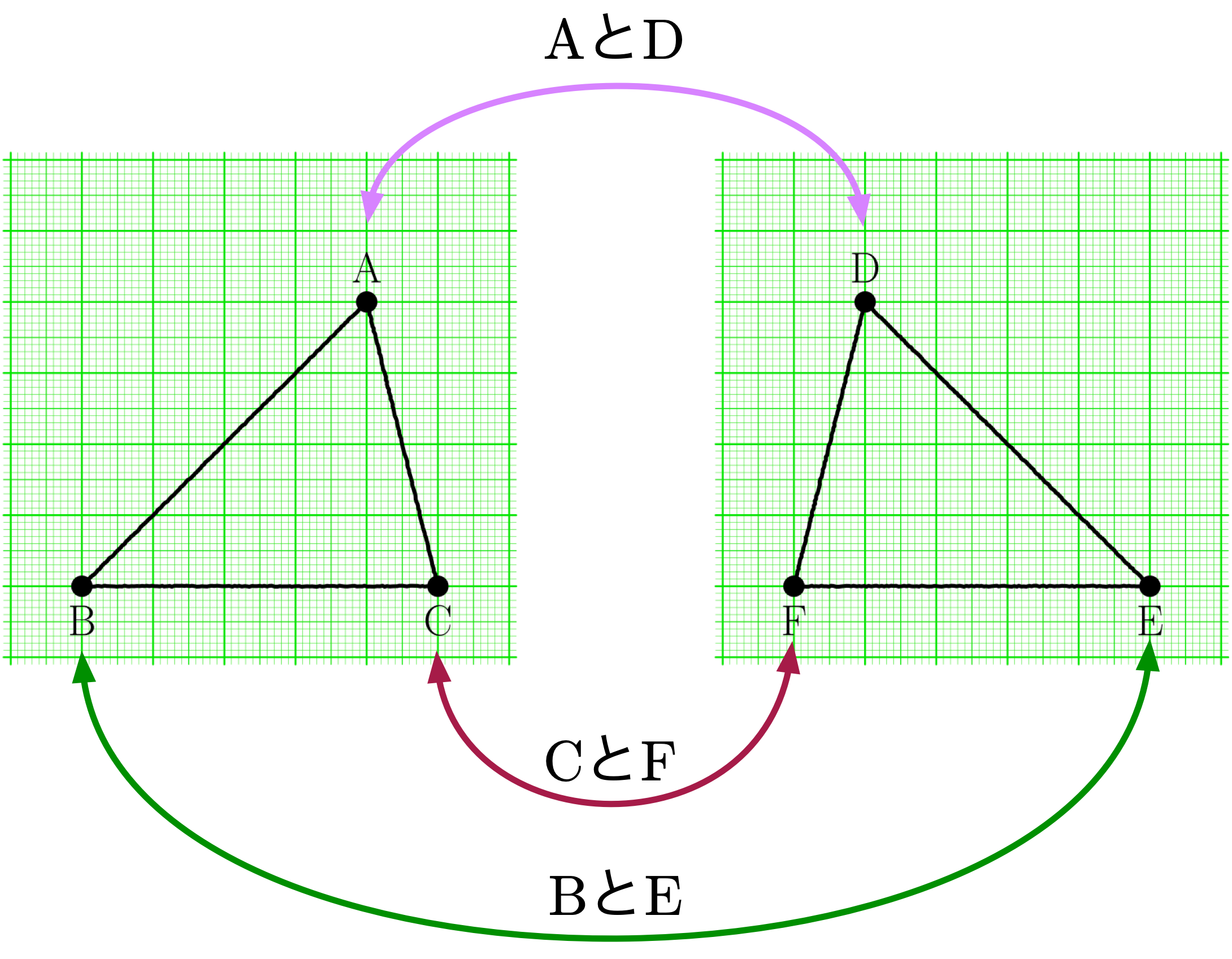
僕「二つの三角形 $\TT{ABC}$ と $\TT{DEF}$ があって、頂点の対応もしっかりつけた。 そうすると自動的に、どの辺とどの辺が対応しているか、どの角とどの角が対応しているかがはっきりするね」
ユーリ「そりゃそーだ」
ノナ「$\NONA$」
ノナは、黙って図の上で指を動かしている。最初は右手の指で両方の三角形を順番になぞり、 それから両手を使って $\TT{ABC}$ と $\TT{DEF}$ を同時になぞる。ゆっくりと。
まるで、図形の対応を味わうみたいに。
僕「……たとえば、三角形 $\TT{ABC}$ のひとつの辺 $\TT{AB}$ に対応している、三角形 $\TT{DEF}$ の辺はどれ？」
ノナ「$\TT{AB}$ だと…… $\TT{DE}$ ですか $\NONAQ$」
ノナは左手で $\TT{A}$ から $\TT{B}$ までなぞると同時に、右手で $\TT{D}$ から $\TT{E}$ までをなぞって答えた。
辺 $\TT{AB}$ に対応している辺は $\TT{DE}$
僕「そうだね、正解！ ノナちゃんは辺 $\TT{AB}$ と辺 $\TT{DE}$ の対応を確かめながら答えたんだね。それはすごく大事なこと」
ユーリ「これって、名前からすぐわかるよね」
ノナ「$\NONAQ$」
ユーリ「ほれほれ、 $\TT{ABC}$ の $\TT{AB}$ だから、 $\TT{DEF}$ なら $\TT{DE}$ じゃん？」
ノナ「だから……ここ $\NONA$」
僕「ユーリが言おうとしているのは、 $\TT{A},\TT{B},\TT{C}$ という頂点がそれぞれ $\TT{D},\TT{E},\TT{F}$ に対応しているんだから、 辺 $\TT{AB}$ に対応している辺は $\TT{DE}$ だとすぐにわかるということなんだよ、ノナちゃん。 名前からすぐわかるってそういう意味だろ、ユーリ？」
ユーリ「そーそー！」
名前の対応から、辺 $\TT{AB}$ と対応しているのは辺 $\TT{DE}$ だと、すぐにわかる
ノナ「まちがい……まちがいですか $\NONAQ$」
僕「いやいや、ノナちゃんのように図で対応を確かめて答えるのはまったくまちがいじゃないし、正しいことだよ。 ユーリのように考えて答えるのもまったくまちがいじゃないし、正しいこと。 どちらでもいいんだよ」
ユーリ「どっちも正解だし！」
ノナ「$\NONA$」
僕「図形が目の前にあるんだから、対応を目視で確認して答えてもいい。 頂点の名前をちゃんと対応付けたんだから、対応する辺の名前は自動的に対応がつくと考えてもいい。 どちらでも100パーセント正しい。どんな方法で考えなくちゃいけないというルールはないからね」
ユーリ「そりゃそーだ」
僕「でも、自分の方法だけが正しいと考えるのはよくないよね。 他の人の方法に耳をすますのも大事。たとえ答えが同じになるとしても」
ユーリ「そーだけど、速く答えが出た方がよくね？」
僕「スピードを競う競技ならそうだね。少しでも速く答えが出た方がいい。 テストなら確かにそうかも」
ユーリ「だよね！」
僕「だとしても、他の方法を知るのはいいことだよ。ひとつの方法で解いたあと、別の方法で確かめることもできるから」
ユーリ「にゃるほど。検算みたいに？」
僕「そうそう、そういうこと」
ノナ「もくしって何 $\NONAQ$」
僕「え？」
ノナ「もくし……もくしって何ですか $\NONAQ$」
僕「……ああ、『目視』ね。『目視』というのは『目で見る』という意味。 目視で確認するというのは、目で見て確認するという意味だよ」
ノナ「わかりました $\NONA$」
僕「じゃあ、もう一つ確認。三角形 $\TT{ABC}$ が持っているひとつの角 $\TT{ACB}$ と対応している、三角形 $\TT{DEF}$ の角はどれ？」
ユーリ「はい、ノナのターン！」
ノナ「$\TT{DFE}$ ……角 $\TT{DFE}$ です $\NONA$」
ユーリ「せいかーい！」
僕「そうだね」
ノナ「目視……目視しました $\NONA$」
僕「うん、いいよ。さっきユーリが言った名前の対応を考えてももちろん同じだね」
ノナ「はい $\NONA$」
角 $ACB$ に対応している角は、角 $DFE$
名前の対応から、角 $\TT{ACB}$ と対応しているのは角 $\TT{DFE}$ だと、すぐにわかる
僕「二つの三角形 $\TT{ABC}$ と $\TT{DEF}$ は合同なので、ぴったりと重ねることができる。 だから、三組の対応する辺の長さはそれぞれ等しくなる。そのことは、こんな三本の式を使って表すことができる」
$\TRI{ABC}$ と $\TRI{DEF}$ が合同のとき、対応する三組の辺の長さはそれぞれ等しい。 $$ \begin{align*} \TT{AB} &= \TT{DE} \\ \TT{BC} &= \TT{EF} \\ \TT{CA} &= \TT{FD} \\ \end{align*} $$
※ここで、たとえば $\TT{AB}$ は、辺 $\TT{AB}$ の長さを表しているとする。 辺 $\TT{AB}$ の長さを $\overline{\TT{AB}}$ のように表すこともある。
ユーリ「カンタン、カンタン！」
ノナ「はい $\NONA$」
僕「$\TT{AB} = \TT{DE}$ という式で表しているのは、 辺 $\TT{AB}$ の長さと、辺 $\TT{DE}$ の長さが等しいということ。それはいいよね？」
ノナ「大丈夫……大丈夫です $\NONA$」
僕「同じように、三組の対応する角の大きさもそれぞれ等しくなる。そのことは、こんなふうに三本の式を使って表すことができる」
$\TRI{ABC}$ と $\TRI{DEF}$ が合同のとき、対応する三組の角の大きさはそれぞれ等しい。（？） $$ \begin{align*} \ANGLE{ABC} &= \ANGLE{DEF} \\ \ANGLE{BCA} &= \ANGLE{EFD} \\ \ANGLE{CAB} &= \ANGLE{EDF} \\ \end{align*} $$
※ここで、たとえば $\ANGLE{ABC}$ は角 $\TT{ABC}$ の大きさを表しているとする。
ユーリ「カンタン、カンタン！」
ノナ「$\NONA$」
僕「三角形には三つの辺と三つの角がある。 二つの三角形が合同ならば、 対応する三組の辺の長さはそれぞれ等しくて、 対応する三組の角の大きさもそれぞれ等しい。 じゃあ逆に……」
ノナ「違う……違います $\NONA$」
僕「え？」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 440本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方／すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加（2020年10月2日）
この記事は『数学ガールの秘密ノート／図形の証明』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ！
![[icon]](https://img.hyuki.net/20220619121014-abd58cfc2ab436f4.png)