第300回 シーズン30 エピソード10

グラフ理論：制約が生む世界（後編）

高校の図書室にて

村木先生の《カード》

ミルカ「……ううっ！」

僕「ミルカさん、どうしたの？」

テトラ「ご気分でも悪いんですか？」

ミルカ「違う。《カード》の裏を見てしまっただけだ……」

僕「裏？　その《カード》の裏に何か書いてあるの？」

村木先生の《カード》（裏面）

ミルカ「……」

僕「『すべての国が、六国以上に隣接する地図を描け。』」

テトラ「これは？」

僕「書いてある通りだね。 どの国を選んでも、隣接国が六国以上ある……そんな地図を描いてみよ、という問題？」

ミルカ「ふむ……思いがけないところにspoilerがいたな」

テトラ「これがspoiler……ネタバレ？　それは、どういうことでしょうか」

僕「隣接国の数というのは、双対グラフの言葉でいうと、まさに《次数》になるから、 この問題はこう言い換えられるよね」

ミルカ「グラフAにこだわりすぎたか（第299回参照）。 spoilerを見てしまう前に、次数を増やしたグラフについて考えるべきだった。 しかし、まずは……」

僕「何はともあれ……」

テトラ「この平面グラフを作ってみるんですねっ！」

ミルカ「そうしよう」

僕「それに、カードの裏にあるこの問題は、《五色定理》のネタバレとは限らないよ。 別の問題かもしれない」

テトラ「あっ、それに、もしかしたら、《五色定理》の方が裏かもしれませんし！」

ミルカ「村木先生の意図を探るよりも、グラフを描こう」

グラフを描こう

テトラ「……これ、無理ですよね？　描いてみましたが……頂点七つのうち、次数が6になる頂点は二つしかできませんっ！」

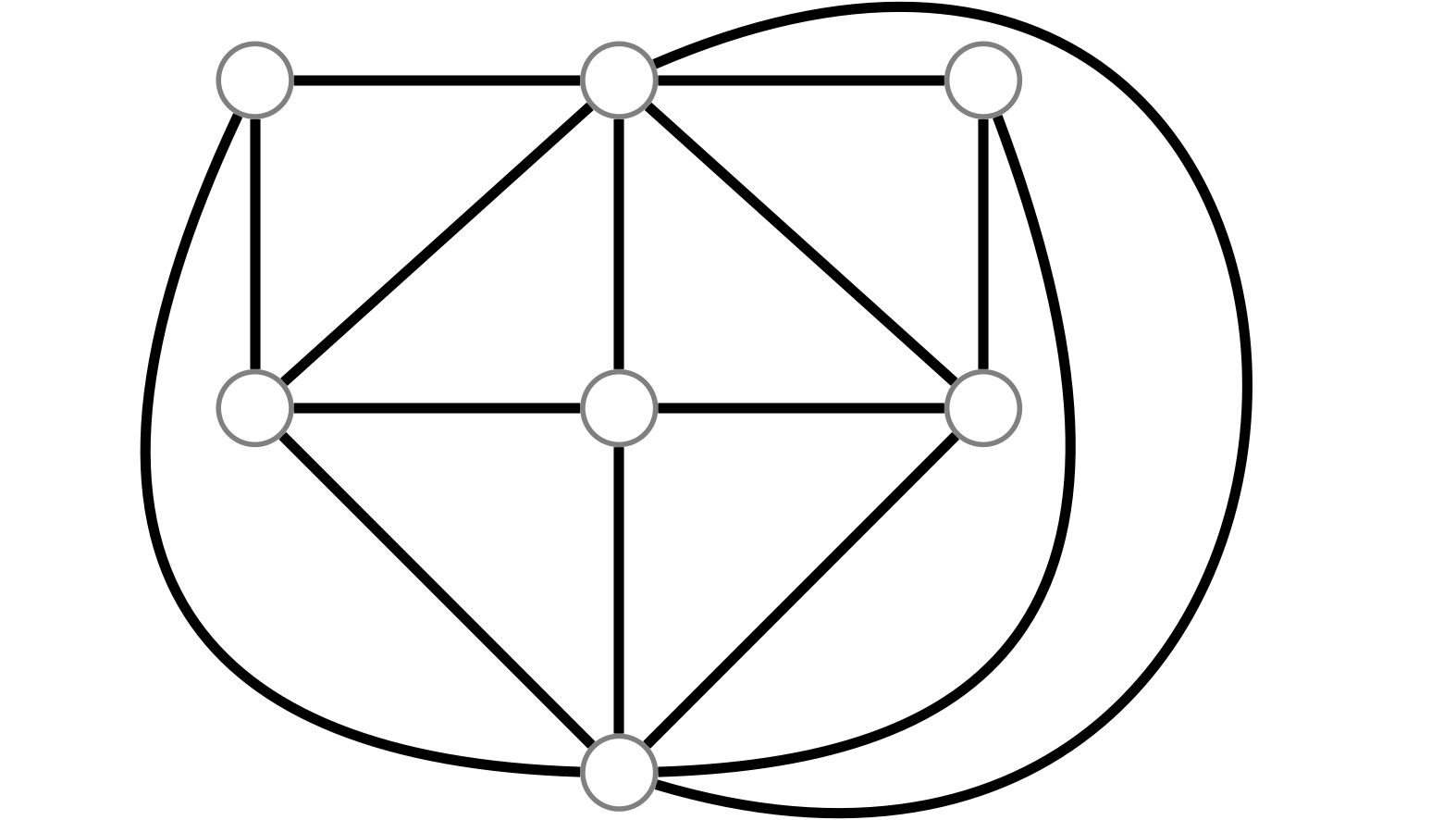
僕「無理だね。僕も似たようなグラフになった。正六角形を描いて、その中心から伸ばせば次数を6にすることはすぐできる。 それから、まわりの頂点の一つを次数6にすることもできる。 でも、そのために辺をたくさん引くことになって、それが壁になってしまう……」

ミルカ「無理だな。私のグラフも同様だ」

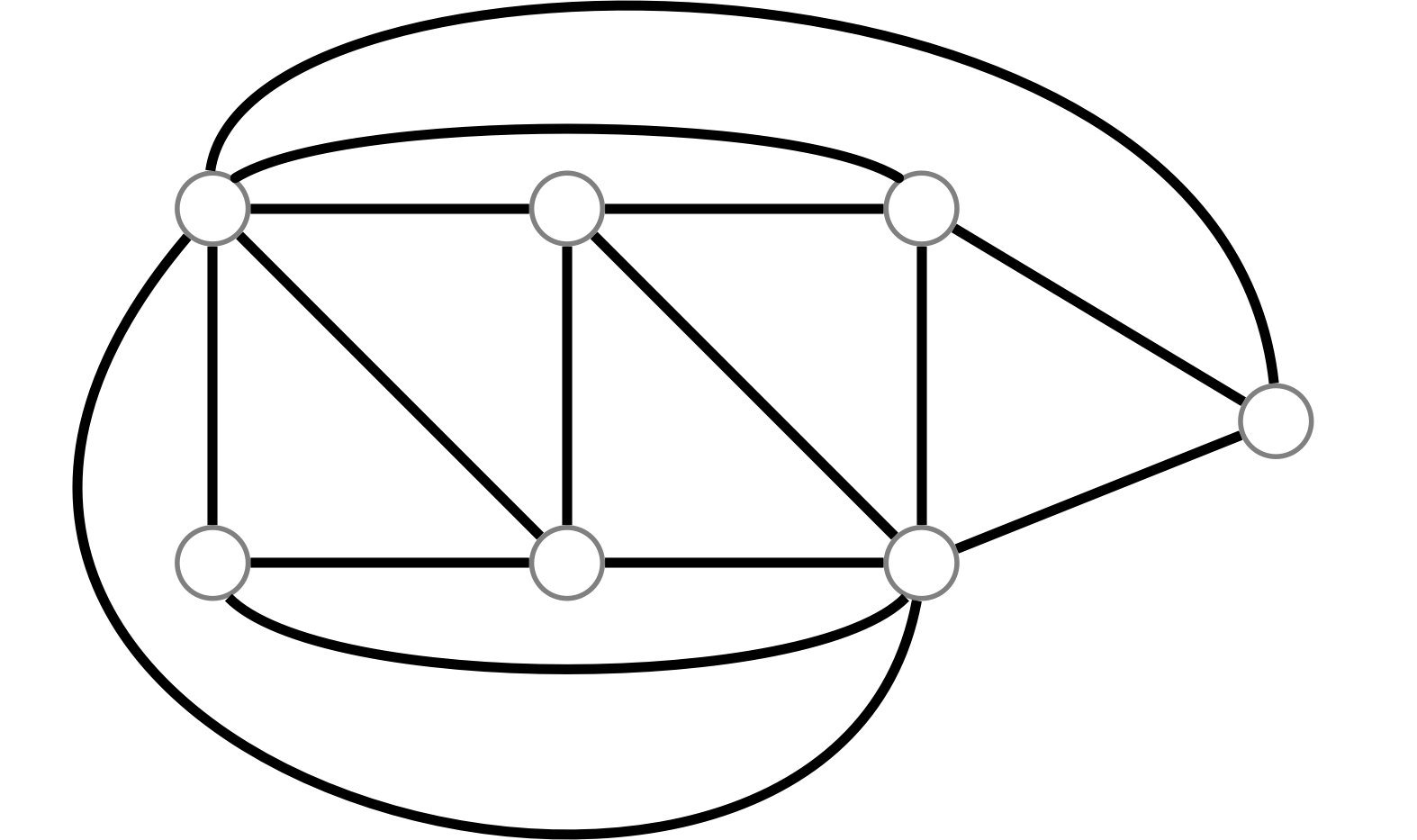
僕「僕たちのグラフ、もしかしてすべて同型じゃない？」

テトラ「えっ」

ミルカ「そのようだな。次数と隣接点を考えれば、こんなふうに対応付けできる」

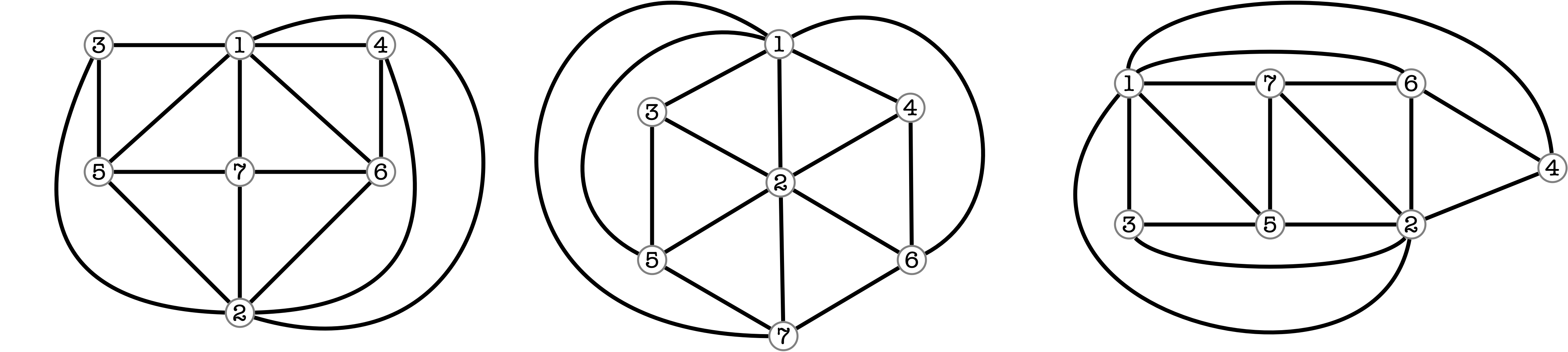
テトラ「やっぱり、村木先生のカードの裏の問題、つまり問題３は不可能……ですよね？」

僕「そうだね。次数を6以上にするためには、少なくとも頂点は七個以上必要。自分以外に六個の頂点がないと次数を6以上にできないから」

ミルカ「ふむ？」

僕「一方、僕たちが考えているグラフの頂点は七個。そしてこのグラフで不可能ならば、これ以上頂点を増やしても不可能」

テトラ「そうですね」

ミルカ「頂点を増やしても無駄だ、とすぐにはいえないな」

僕「だって、頂点を増やしても混雑するだけで、辺はかえって増やせなくなる」

ミルカ「それでは論証にならない。たとえば、私たちのグラフで次数が3の点のそばに新たな頂点を三個増やして辺で結べば、 その頂点の次数は簡単に6に増やせる」

僕「いやいや、それはそうだけど、 いま増やした新たな頂点に関しては次数1になってしまうよね。だから、やっぱりだめだよ。その新たな点も次数6以上にしなくちゃいけないんだから」

ミルカ「だからこそ論証が必要になるわけだ」

僕「確かにそうだけど……」

ミルカ「私たちは問題３の例を作ろうとして、不可能という予想を立てた。 だから次に進む方向はもちろん……」

僕「証明する方向だね」

テトラ「すべての頂点の次数が6以上になるような、そんな平面グラフは存在しない……ことを証明する？」

テトラ「……これは、見当も付きません。第一歩からわかりません。 というか、第一歩は例を作ることで、それはもう済ませました。 そこから予想が出てきましたし、この主張の意味もよくわかっています。 でも……《証明としての第一歩》はどうしたらいいんでしょう」

証明としての第一歩はどうしよう？

僕「……」

テトラ「だって、平面グラフは無数に存在します。 ちょっと辺を足したり、ちょっと頂点を付け加えれば、 ものすごく複雑なものまで作れますよね。無限に作れてしまいます。 もちろん《いかにも無理そう》というのはわかりますけれど」

ミルカ「無限には、論理で立ち向かう」

テトラ「論理……」

僕「僕たちが証明でよく使うのは二つだよね。 《数学的帰納法》か《背理法》か。 すべての正の整数について何かを証明したかったら《数学的帰納法》が使えないかと考えるのは自然」

テトラ「《背理法》は……証明したいことの否定を仮定して、矛盾を導くんですよね」

僕「そうだね。《背理法》は難しいけれど、慣れれば考えやすくなる。 たとえば、僕たちはいま、

　○○○○が成り立つ平面グラフは存在しない

を証明したい。でも一つ一つ平面グラフを試して○○○○が成り立つかどうかを調べるのは大変」

テトラ「はい……はい、そうでした。《背理法》では、

　○○○○が成り立つ平面グラフが存在する！

と仮定して話を進めていって、どこかで出てくるはずの矛盾を見つけるんですね」

僕「そうだね。それが考えやすいのは、《○○○○が成り立つ平面グラフ》を使って、 議論を前へと進めることができるから」

テトラ「前へと進める……なるほど。 今回の場合には、

　すべての頂点の次数が6以上になる平面グラフは存在する！

と仮定して話を進めることになります。 で、でも《すべての頂点の次数が6以上》ということから何が言えるのでしょう……」

僕「そうだなあ……」

ミルカ「すべての頂点の次数が6以上……ということは《次数の総和は、辺の数の二倍》が使えるな」

僕「確かに！」

テトラ「先ほどミルカさんがおっしゃっていた《自明な事実》ですね（第299回参照）」

ミルカ「そうだ。 《次数の総和は、辺の数の二倍》とは、 あるグラフの次数の総和を $D$ で表し、辺の本数を $E$ とすると、 $$ D = 2E $$ がいえるということ」

僕「グラフのどの頂点についても次数は6以上だと仮定すると、 $6V = D$ になるよ。あ、違う、不等式だ。 $$ 6V \LEQ D $$ だね」

テトラ「あっ、急に見通しがよくなりました。 $$ 6V \LEQ D = 2E $$ ということですよね。としたら、あたしたちのグラフではこんな不等式が成り立つことになりますね？」

$$ 3V \LEQ E \qquad \cdots\cdots\REMTEXT{☆} $$

僕「そうだね」

テトラ「でも、あたしたちはここから矛盾を導かないといけないんですよね……この不等式はいったい何に矛盾するんでしょう」

ミルカ「《条件をすべて使ったか》だな。 私たちのグラフには強い制約があった。連結な平面グラフという制約だ。だから……」

僕「だから、うん、そうだね。わかったよ……」

テトラ「連結な平面グラフという制約から……矛盾を導く？」

僕「連結な平面グラフで成り立つ定理から出てくる、ある不等式と矛盾するんだよ」

テトラ「連結な平面グラフで成り立つ定理……ああ、オイラーの多面体定理！（第298回参照）」

僕「そうだね。 僕たちはそこから $F$ を消した不等式を知ってる！」

テトラ「はいっ、知ってます！　これです。 $$ 6 \LEQ 3V - E \qquad \cdots\cdots\REMTEXT{★} $$ ……ああ、でもこれは使えませんでしたよね。 これは、具体的な数を当てはめても成り立ってしまう不等式でしたから、矛盾は出ませんよね？」

僕「違う違う。それは二部グラフの判定のときのこと（第298回参照）。 今度は違う。不等式 $3V \LEQ E$ と $6 \LEQ 3V - E$ を使えば矛盾が出せるよ、テトラちゃん！」

テトラ「……そうですか？　この二つから矛盾？」

僕「そうだよ、だって（むぎゅ）」

テトラ「……わかりました！　確かに矛盾してます！　★の不等式、 $$ 6 \LEQ 3V - E $$ から、いくつか移項すると、 $$ E \LEQ 3V - 6 $$ が言えますので、☆の $3V \LEQ E$ を合わせると、 $$ 3V \LEQ E \LEQ 3V - 6 $$ となります。 $3V \LEQ 3V - 6$ なんてあり得ません。 $0 \LEQ -6$ ということですから。矛盾です！」

ミルカ「これで、連結な平面グラフでは「どの頂点についても、次数は6以上」は偽であることがいえた」

僕「（ぷはっ）ああ苦しかった。……そうだね」

ミルカ「これで、私たちはカード裏面の問いに答えることができたわけだ」

僕「すべての国が、六国以上に隣接する地図を描くのは不可能」

ネタバレ？

テトラ「ところで、実際のところ、すべての頂点の次数を6以上にするのは不可能だとして、 これは《五色定理》の証明に関するネタバレになっているんでしょうか」

僕「すべての頂点の次数を6以上にすることはできないのはわかったけど、 それがどんな手がかりになるかってことだね」

ミルカ「大きな手がかりだな。なぜかといえば、《すべて》を否定すると《存在する》が出てくるからだ。 次の二つは同値」

• 連結な平面グラフでは、すべての頂点の次数を6以上にすることはできない。
• 連結な平面グラフには、次数が5以下の頂点が存在する。

テトラ「《次数が5以下の頂点》が存在する。 《五色定理》の証明ではこれが鍵になる？　……かどうかは、まだわかりませんよね」

ミルカ「わからない。しかし、『連結な平面グラフの頂点が何個であったとしても《次数が5以下の頂点》が存在する』という主張は助かる。 この頂点を使って考えを進めることができるからだ」

僕「確かに。その発想は背理法のときと一緒だね。《次数が5以下の頂点》に注目するわけだ！」

テトラ「ちょっと整理させてください。あたしたちは……」

• あたしたちは《五色定理》を証明しようとしています。
• 《五色定理》、つまり、連結な平面グラフは五彩色可能であるという定理です。
• 言い換えると、任意の《連結な平面グラフ》の頂点彩色には五色あれば十分という定理です。

僕「そうだね」

テトラ「そして、あたしたちがいま手に入れた《武器》はこれですっ！」

• 連結な平面グラフには、次数が5以下の頂点が存在する。

僕「……」

テトラ「……」

ミルカ「……」

僕「次の一歩は、数学的帰納法かな。頂点数に関する数学的帰納法だね、 僕たちはすでにこれを証明している（第299回参照）」

• 頂点数が5以下の連結な平面グラフはすべて五彩色可能である。

テトラ「そうですね」

僕「だから、あとはこれを証明すればいい」

• 《頂点数が $n$ 以下の連結な平面グラフはすべて五彩色可能である》と仮定すると《頂点数が $n+1$ の連結な平面グラフはすべて五彩色可能である》。