![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
パズル
図のように平面上に六個の頂点があります。
三個の頂点には $A,B,C$ とアルファベットで名前が付けられており、 残りの三個の頂点には $1,2,3$ と数字で名前が付けられています。
アルファベットで表された三頂点と数字で表された三頂点を辺で結びます。
$A$ は $1,2,3$ すべてとつながり、 $B$ も $1,2,3$ すべてとつながり、 $C$ も $1,2,3$ すべてとつながるように辺を描きます。
辺は直線でも曲線でも構いませんが、 辺を交差させて描いてはいけません。
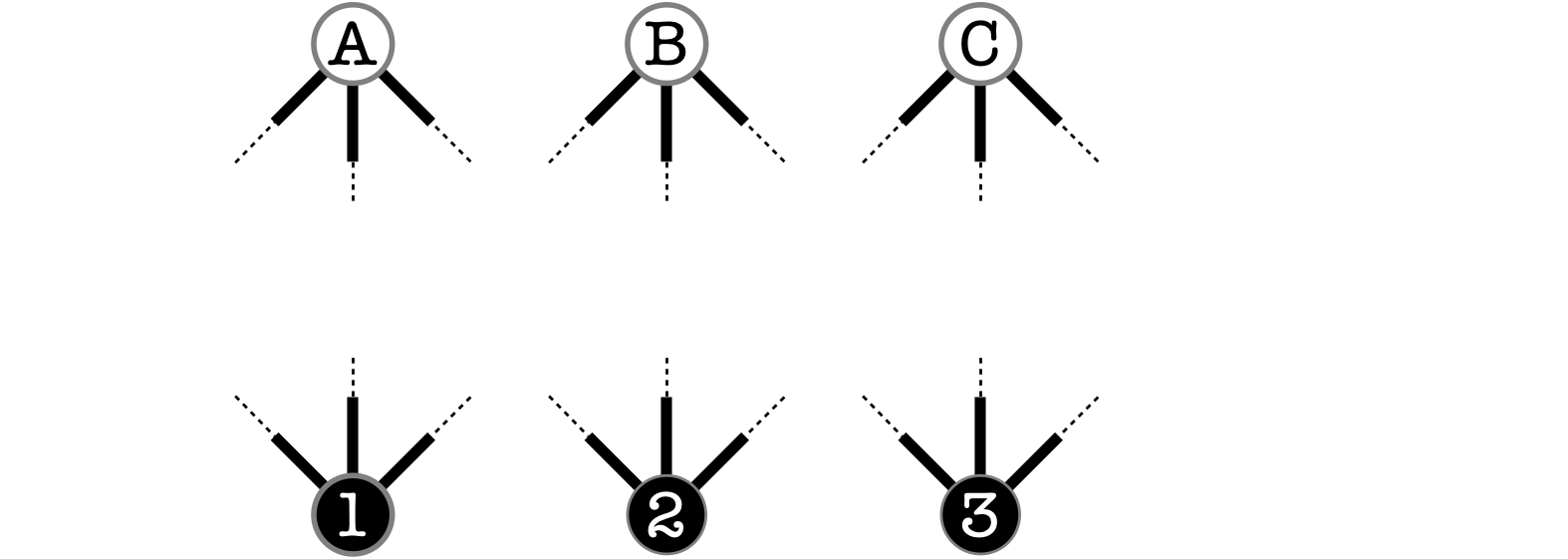
これは可能でしょうか(第297回参照)。
いくつか試行錯誤したけれど、失敗した様子

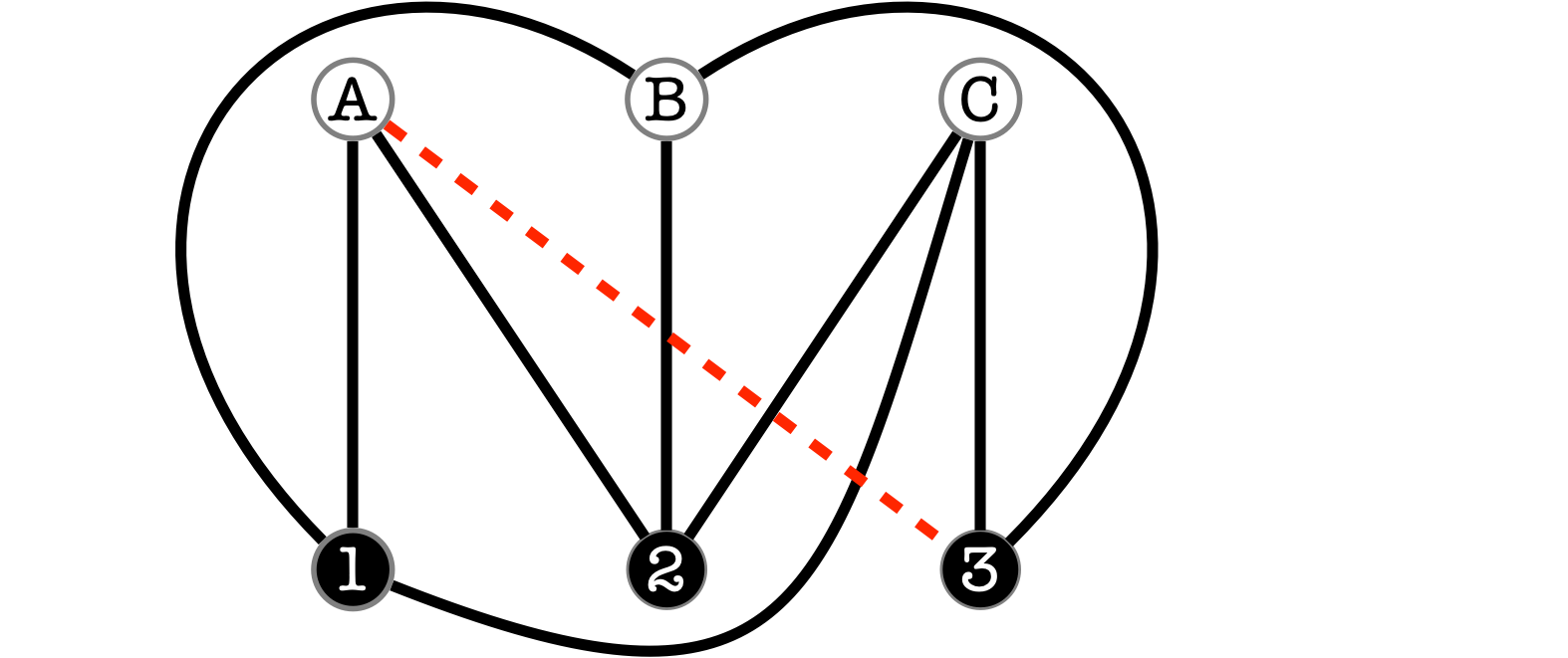
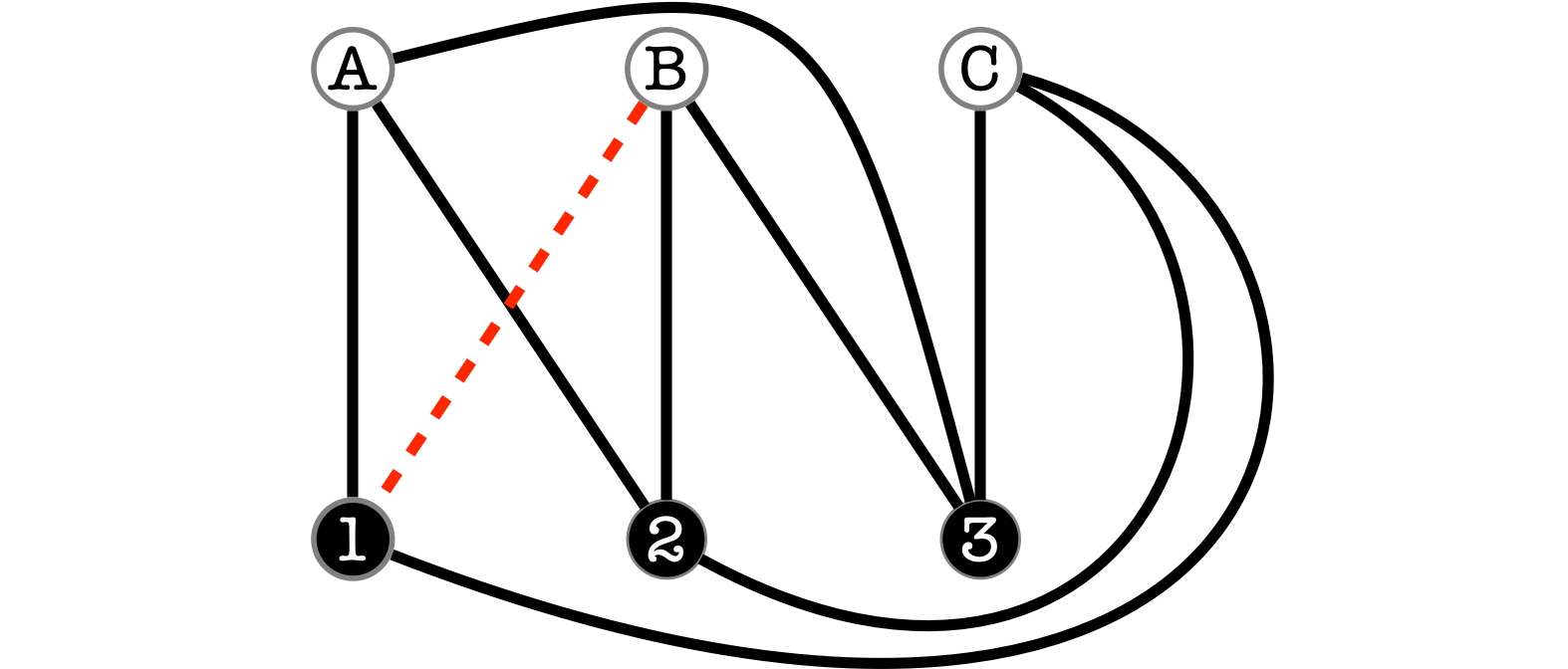
僕は、この《パズルのグラフ》を、辺が交差しないように描くのは不可能だと「証明」した。
でもテトラちゃんが「引っかかる」というので、より明確な証明を探そうとしていた。
辺を交差させずに描けるグラフ……平面的グラフ……の例をいくつか作りながら検討を続けていた。
そのうちに、ふとしたことから話題が寄り道にそれていって……(第297回参照)
僕「……ごめんごめん。 僕はぜんぜん《パズル》とは別のことを考えていたんだ。 立方体を押しつぶす話。ミルカさんから聞いたんだけど」
テトラ「立方体を押しつぶす……って、どんなお話でしょう」
僕「立方体をべちゃっと平面上に押しつぶす。こんなふうにね」

テトラ「これは、左の立方体を上から押しつぶしたようすですか?」
僕「そうそう。そんなふうに押しつぶしても、頂点の数や辺の数は変わらない。 それから、つながり方も変わらない。 立方体の底面、この図だと6番の面は、押しつぶしたらなくなっちゃうみたいだけど、 外側全体の領域を一つの面と考えるなら、 つじつまがあっているといえる」
テトラ「つじつまがあっている……?」
僕「ああ、うん、どの面とどの面が接しているか、その境界にあたる辺はどれか……という《つながり方》は押しつぶしても変わらないよね。 たとえば、6番の面は、2,3,4,5番の面と接している。 トポロジーの話題になったとき、ミルカさんは、 そんなふうに《つながり方》を変えずに立方体を押しつぶす話をしてくれたことがあったんだ(『数学ガール/ポアンカレ予想』参照) ……あれ、ちょっと待って?」
テトラ「?」
僕「ちょっと待って。それを使えないかな?」
テトラ「それ……?」
僕「立方体をつぶして平面にしちゃうんだよ! 立方体は連結グラフだと思うことができる。 頂点があって、二つの頂点のあいだに辺がある。ループはないし、多重辺もない。 立方体は平面につぶせるから、平面的グラフといえる。辺が交差しないように立方体をつぶせるからね」
テトラ「立方体の頂点は八個で、辺は十二本あります。 小さな例から少しずつ考えてきましたが、急に大きな例にしちゃうんですか……?」
テトラちゃんは、用心深そうな声を出した。
僕「うん、ちょっと例の大きさはさておく。 思いついたのは、 立体となったグラフを平面につぶすというアイディアなんだ。 例を作っているときには、辺で囲まれたところを《領域》と呼んでいたから気付かなかった。 《面》と呼べば気付いたかもしれない!」
テトラ「ええっと……何に気付いたんでしょう?」
僕「オイラーの多面体定理だよ!」
オイラーの多面体定理
穴が空いていない多面体の頂点の数を $V$ とし、辺の数を $E$ とし、面の数を $F$ とすると、 $$ V - E + F = 2 $$ が成り立つ。
※V, E, Fはそれぞれ頂点(vertex(複数形vertices))、辺(edge)、面(face)の頭文字。
テトラ「オイラーの多面体定理……え、ちょっと意味がわかりません。 $V - E + F = 2$ という等式が成り立つということですか」
僕「そうだよ。割と有名な等式だね。 個数の関係を表しているだけだから、主張自体はそんなに難しくないと思うけど」
テトラ「あ、いえ、意味はわかります。 あたしが言いたかったのは『こんな等式がほんとうに成り立つの?』ということです」
僕「驚きだよね」
テトラ「た、試してみます。立方体の頂点は $8$ 個で、辺は $12$ 本で、面は $6$ 個ですね。

つまり、 $$ V = 8, \quad E = 12, \quad F = 6 $$ です。 $V - E + F$ を計算すると…… $$ V - E + F = 8 - 12 + 6 = 2 $$ ……ほんとですね!!」
僕「立方体に限らないし、正多面体とも限らないよ。たとえば四角錐を考えると、

頂点は $5$ 個、辺は $8$ 本、面は $5$ 個だから、 $$ V = 5, \quad E = 8, \quad F = 5 $$ になる。 $V - E + F$ を計算すると…… $$ V - E + F = 5 - 8 + 5 = 2 $$ ……になるね」
テトラ「あららら……」
僕「たとえば、こんな適当な多面体でもいいよ」

テトラ「数えてみます…… $$ V = 7,\quad E = 12,\quad F = 7 $$ ……ですね。 $$ V - E + F = 7 - 12 + 7 = 2 $$ はい、確かに成り立ちます。 これは、驚きですっ! ……驚きなんですが、 これが《パズルのグラフ》と関係があるんでしょうか?」
僕「そうそう、そうだった。 あのね、さっきは立方体を押しつぶしたけど、 その逆をやってもいいよね。辺が交差しない、平面に描かれたグラフがあったとする。 そのグラフを立体に持ち上げて、外周に面を張る」
テトラ「……」
僕「そのような操作をしても、頂点の数・辺の数・面の数には変わりはないし、 つながり方も変わらない」
テトラ「あっ、わかりました。ということはオイラーの多面体定理が成り立つ?」
僕「その通り! 僕たちはいま《パズルのグラフ》が平面に描けるかどうかを考えていた」
テトラ「はい。平面的グラフになるかどうか……」
僕「話を簡単にするために、連結グラフに限定して考えていた。 つまり最初からばらばらになったグラフは除外して考えていたから、 オイラーの多面体定理を使うと、こんなことがいえる」
連結グラフに限定して考える。
平面的グラフならば、 $$ V - E + F = 2 $$ が成り立つ($\heartsuit$)。
テトラ「あっあっ! これで判定ができるんですね」
僕「うん、そうだね。 《平面的グラフならば、 $V - E + F = 2$》はいえる。 あ、ちょっと待って……うん、大丈夫」
テトラ「?」
僕「平面的グラフで、 面を作らない辺が枝のように伸びていたとしても大丈夫かなと思ったんだけど、 大丈夫だった。面を作らない辺が枝のように伸びているときは、 $V$ と $E$ は同数で増えるから、影響はない。 だから《平面的グラフならば、 $V - E + F = 2$》はいえる。 逆の《$V - E + F = 2$ ならば、平面的グラフ》かどうかはわからないけれどね」
テトラ「あれ……でも、あたしたちが知りたいのは《パズルのグラフ》が平面的グラフかどうかですから、 《平面的グラフならば……》という定理があっても使えないんじゃありませんか?」
僕「そうじゃないんだよ。 $\heartsuit$ の対偶を考えればすぐにわかる」
($\heartsuit$)平面的グラフならば、 $V - E + F = 2$ が成り立つ。
($\heartsuit$ の対偶)$V - E + F = 2$ が成り立たないならば、平面的グラフではない。
テトラ「なるほど……平面的グラフではないという判定に使えるんですね?」
僕「そうそう。 命題とその対偶の真偽は必ず一致するからね」
テトラ「ということは《パズルのグラフ》で、 $V - E + F$ を《計算》して、 $2$ にならないなら、 つまり、 $$ V - E + F \NEQ 2 $$ がいえれば証明完了ですねっ! $V - E + F$ って、何て素敵な式でしょう!」
僕「さっそく計算してみよう!」
僕とテトラちゃんは計算を始めようとした。
でも、すぐに行き詰まってしまった。
テトラ「先輩……」
僕「困った……」
テトラ「《パズルのグラフ》では、頂点の数は $V = 6$ で、 辺の数は $E = 9$ ですが……」
僕「面の数がわからないね……」
テトラ「はい。そもそも平面に描けないんですから……面?」

そこに、ミルカさんが現れた。ピアノ少女エィエィといっしょだ。
登場人物紹介(追加)
ミルカさん:数学が好きな高校生。 僕のクラスメート。長い黒髪の《饒舌才媛》。
エィエィ:ピアノが得意な高校生。ミルカさんと仲がいい。
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2020年7月24日)