![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
高校生の僕と中学生のユーリは《連結ゲーム》を楽しんでいた(第291回参照)。
僕の必勝法を見抜いたユーリは、 ほんとうにそれが必勝法になっているかを証明しようとしている。
《連結ゲーム》のルール
プレイヤーは二人。 紙に $1$ 個以上の頂点を描き、交互に二頂点を結ぶ辺を描く。 先に描けなくなったプレイヤーが負けである。
辺を描くときのルールが三つある。
ルール1:辺は多重にしない
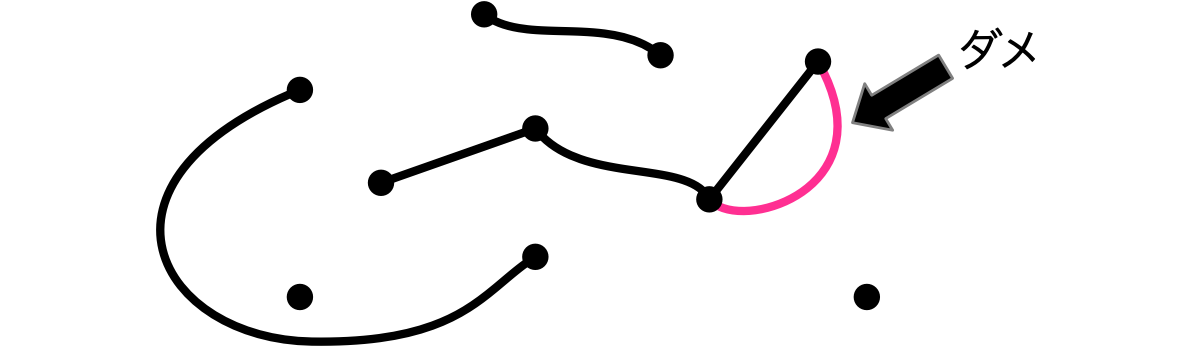
ルール2:ループを作らない
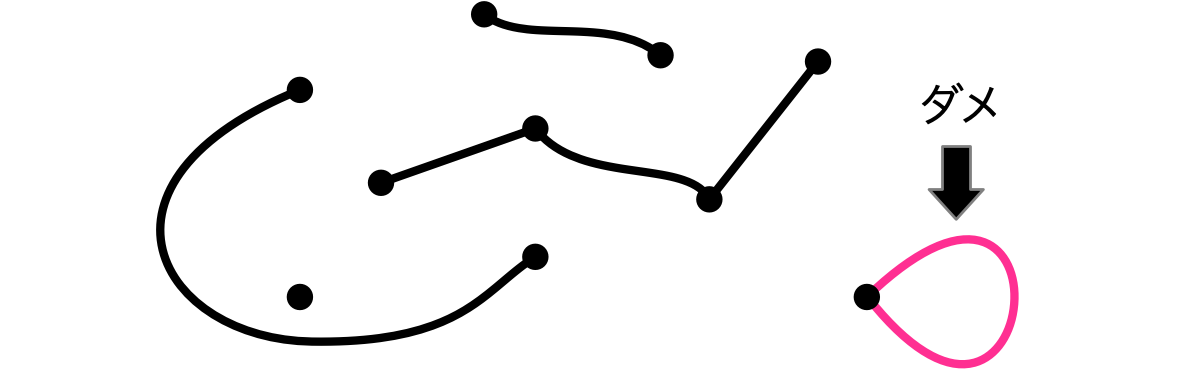
ルール3:サイクルを作らない
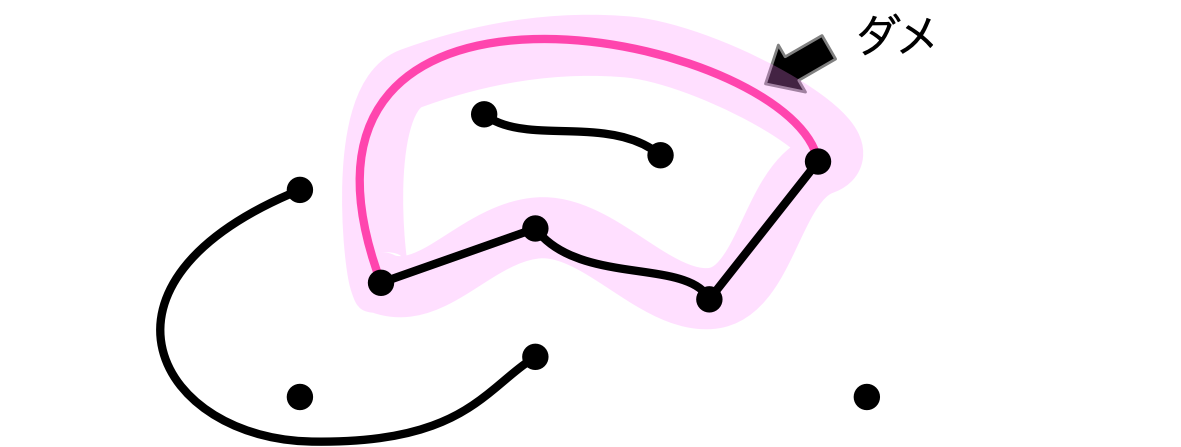
僕「ユーリが推理した必勝法はこういうことだね。でも、推理は推理に過ぎない。証明しないと」
ユーリの推理
《連結ゲーム》では、最初に描いた頂点の数で勝者が決まる。
ユーリ「お兄ちゃんが言った通り、小さい数で試したよ! まず、頂点が $1$ 個だと、後手必勝!」
頂点が $1$ 個の場合
頂点が $1$ 個の場合、もう辺は描けない。 無理に描こうとするとループになってしまうので《ルール2》に反する。 だから、先手になった方が負ける。

$1$ は奇数だから、確かに「奇数個ならば、後手必勝」になっている。
僕「頂点が $2$ 個の場合は、先手必勝だね」
頂点が $2$ 個の場合
頂点が $2$ 個の場合、先手が結ぶ辺は一種類しかない。
後手がさらに無理に描こうとすると辺が多重になるか、ループになってしまう。
辺が多重になったら《ルール1》に反する。

ループになったら《ルール2》に反する。
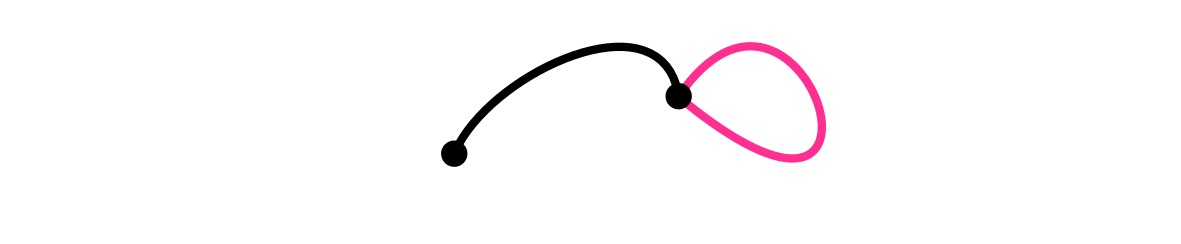
だから、後手になった方が必ず負ける。
$2$ は偶数だから、確かに「偶数個ならば、先手必勝」になっている。
ユーリ「ははーん……」
僕「何か気がついた?」
ユーリ「頂点が $1$ 個の場合、頂点が $2$ 個の場合と来たら……」
僕「と来たら……」
ユーリ「お兄ちゃんの大好きな一般化だ! 頂点が $n$ 個の場合を考えるんでしょ? でしょでしょ?」
僕「ええっ?」
ユーリ「へ? 違うの?」
僕「いや、それは《早すぎる一般化》だと思うよ。 $1$ 個、 $2$ 個と来たら、頂点が $3$ 個の場合も考えようよ」
ユーリ「えー、めんどいよー」
僕「頂点が $3$ 個の場合、どんなふうに《連結ゲーム》が進むか考えてみよう」
頂点が $3$ 個の場合

ユーリ「あー、先手は $3$ 通りあるじゃん?」
頂点が $3$ 個の場合、先手ははじめに $3$ 通りの辺を描くことができる

僕「うん、確かに $3$ 通り描けるけれど、つながり方を考えると、実質的には $1$ 通りしかないと考えてもいいよね」
頂点が $3$ 個の場合、先手が描ける辺は実質的に $1$ 通り

ユーリ「あ、そーだね。どこかの $2$ 点がつながるだけだから」
僕「これに対して、後手の描き方は?」
ユーリ「後手は……うん、これは $2$ 通りあるけど、ジッシツテキには $1$ 通り? 裏返して考えたら」
頂点が $3$ 個の場合、後手が描ける辺は $2$ 通りあるけれど……

僕「うん、 $1$ 通りだね。裏返してもいいし、鏡に映してもいい」
頂点が $3$ 個の場合、後手が描ける辺は実質的に $1$ 通り
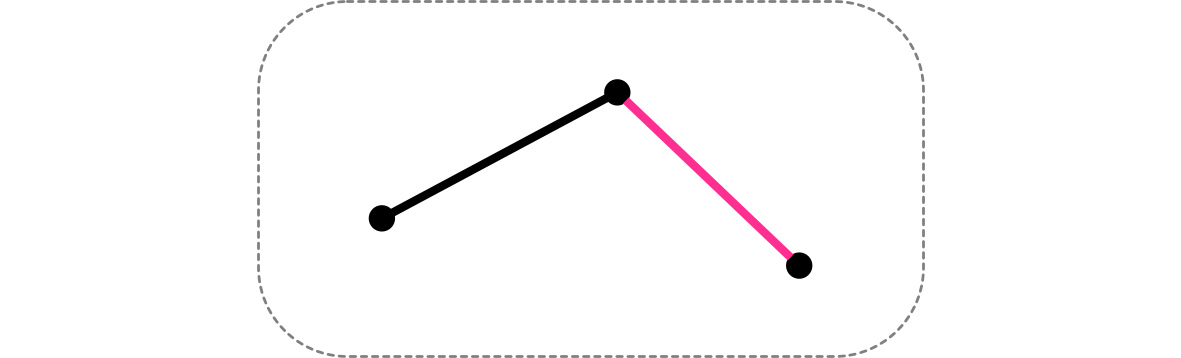
ユーリ「これでもう先手は描けないから勝負あった! 頂点が $3$ 個のときは後手必勝だ!」
僕「うん、そうだね」
頂点が $3$ 個の場合
頂点が $3$ 個の場合、先手が描ける辺は実質的に一種類しかない。
それに対して後手が描ける辺も実質的に一種類しかない。
それに対して先手が描ける辺はない。
だから、先手になった方が必ず負ける。
$3$ は奇数だから、確かに「奇数個ならば、後手必勝」になっている。
ユーリ「さてさて、お待ちかねの一般化!」
僕「いやいや、まだ具体例を考えていこうよ」
ユーリ「どしたのお兄ちゃん。いつもならそろそろ《文字の導入による一般化》じゃあ! って腕まくりするとこじゃん? キャラ壊れたの?」
僕「だって、まだこれじゃ一般化できそうにないからね」
ユーリ「えー、そっかなー。だっていつもなら《頂点が $n$ 個の場合》から《頂点が $n + 1$ 個の場合》へと華麗に進むでしょー?」
僕「ユーリがいってるのは、《数学的帰納法》を使うって意味だよね」
数学的帰納法
どんな正の整数 $n$ についても条件 $P(n)$ が成り立つことを証明するには、次の二つのステップを踏めばいい。
ステップA: $P(1)$ が成り立つことを証明する。
ステップB:任意の正の整数 $n$ について「$P(n)$ が成り立つならば、 $P(n + 1)$ も成り立つ」ことを証明する。
ユーリ「それそれ、そーゆーやつ。ステップAはめっちゃ簡単で、ステップBが華麗なやつ」
ユーリ「奇数と偶数、交互に進むから、簡単に証明できんじゃないの?」
ユーリの推理
《連結ゲーム》では、最初に描いた頂点の数で勝者が決まる。
これを証明したい!

僕「……うん、大まかにはわかってきたけど、やっぱり《頂点が $4$ 個の場合》を考えよう」
ユーリ「へいへい、お兄ちゃんには逆らえませんな。 $4$ 個並べますとも」
頂点が $4$ 個の場合

僕「まず先手は……」
ユーリ「先手は、えーと……何通り?」
僕「つながり方を考えれば、この $1$ 通りだよ」
頂点が $4$ 個の場合、先手の描き方
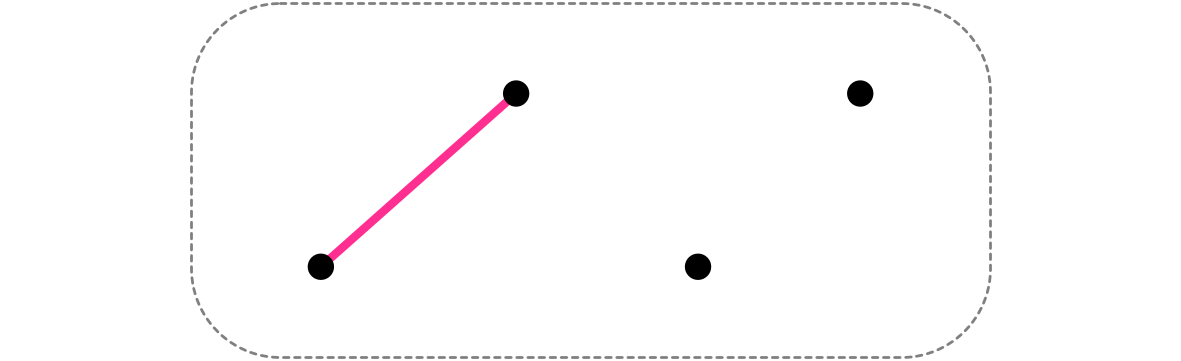
ユーリ「あー、そっか。そーだね……」
僕「単純化して進まないと、考える場合の数が増えちゃうから気を付けないと」
ユーリ「次は後手でしょ。後手も $1$ 通り……んにゃ! $2$ 通りある! 辺をつなげるのと、辺をバラけさせるのと」
頂点が $4$ 個の場合、後手の描き方

僕「次は先手に戻るんだけど、二つの場合のそれぞれを考えなくちゃいけなくなる……」
ユーリ「うわあ……すでにめんどくさい……」
僕たちは、議論しながら先手のパターンを調べて、①②③を得た。
頂点が $4$ 個の場合、先手の描き方
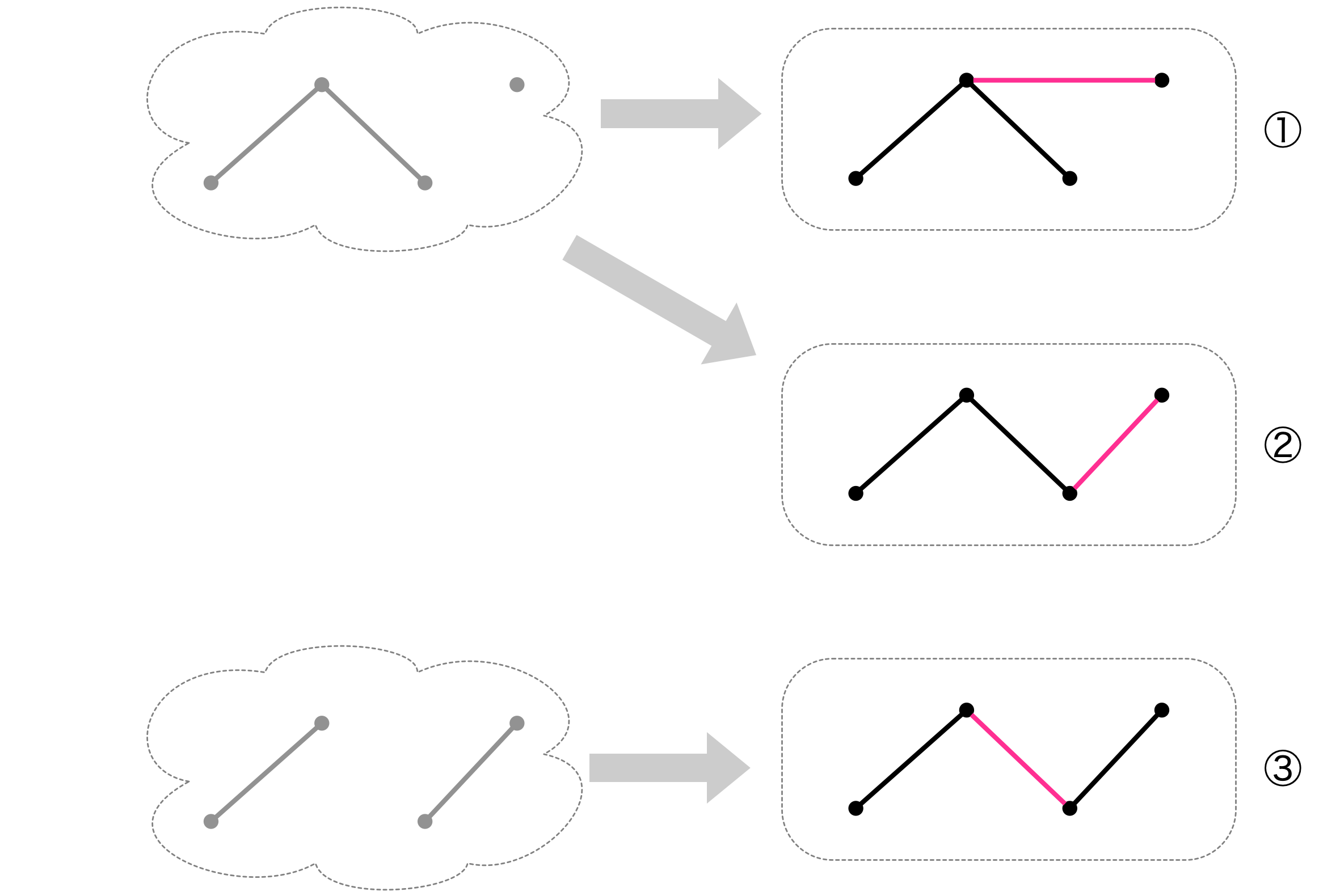
僕「……あれ?」
ユーリ「②と③のジグザグは結局同じだよね?」
僕「そうだね。つまり、頂点 $4$ 個から始めて、先手→後手→先手と来たときにできるグラフは、この $2$ 通りになる。そしてこれ以上は辺は引けない」
頂点が $4$ 個の場合、勝負が付くパターンは $2$ 通りある

ユーリ「そっかー、場合の数がぞくぞく増えるようだけど、実際は同じになったりするんだね! んじゃ、そろそろ一般化に参りますか」
僕「そうだね。じゃあ、証明するよ。まず……」
ユーリ「まって。ユーリ、謎を解いちゃったもん!」
僕「え?」
ユーリ「あのね、ユーリは名探偵なのじゃ。すでに謎はすべて解けておるのじゃ。まずは聞きたまえ」
僕「聞いてるよ」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 430本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2020年6月12日)