第278回 シーズン28 エピソード8

放物線をつかまえて：ボールに隠されてるもの（後編）

高校にて

僕「……うん、これで《力学的エネルギー保存の法則》が導けたことになる！　左辺は初期状態、つまり時刻 $0$ における力学的エネルギーで、 右辺は任意の時刻 $t$ における力学的エネルギーになっているから」

ミルカ「そういうこと」

僕「確かに自然に導けるんだなあ」

テトラ「……あの、テトラはまだ引っかかっているようです」

僕「おや？」

テトラ「い、いえ、ミルカさんの式変形はわかりましたし、意味もわかっています。 《ニュートンの運動方程式》と《万有引力の法則》から求めた $h(t)$ と $v(t)$ を使って、 《力学的エネルギー保存の法則》は確かに導けました。 《力学的エネルギー保存の法則》が、いわば定理だということもよく理解しました」

ミルカ「ふむ？」

テトラ「でも……《力学的エネルギー保存の法則》というのは、 《力学的エネルギー》が《保存》される法則ですよね。 先ほどの等式で、《保存》の方は納得しました。 あたしがまだ引っかかっているのは《力学的エネルギー》の方です」

僕「え？」

テトラ「ミルカさんの式変形の途中で、こんな式が出てきました（第277回参照）。 $$ v^2_0 + 2gh_0 = v(t)^2 + 2gh(t) $$ あたしには、この式が、すでに《保存》を表しているように見えます。 だって左辺と右辺は同じ形ですから。そうですよ。こう書いてもいいですよね。 $$ v(0)^2 + 2gh(0) = v(t)^2 + 2gh(t) $$ これは《保存》を表す式です。つまり、 $$ v(t)^2 + 2gh(t) $$ という式は《保存量》を表しています！」

僕「そうだけど、 $\frac12m$ 倍しても《保存量》であることは変わらないよ」

テトラ「それはわかります。 でも、恣意的に $\frac12m$ 倍されるところがどうしても引っかかります。 文字を増やしてまでどうしてそんなことをするのか。 あたしが知りたいのは、 $\frac12m$ 倍するどんな必然性があるのかということなんですっ！」

ミルカ「ふむ……」

僕「必然性といっても……」

ミルカ「極論をいえば、必然性はないな」

テトラ「ないんですか！？」

ミルカ「力学的エネルギーという概念を考える必然性もないし、それが $\frac12mv(t)^2 + mgh(t)$ で表される必然性というものもない。 しかし、そう考えるとうれしい場面はたくさんある」

テトラ「確かに、あたしが《必然性》と表現したのは不適切だった……かもしれません。 でも、 $v(t)^2 + 2gh(t)$ も《保存量》であることは正しいですよね」

ミルカ「もちろん。 $v(t)^2 + 2gh(t)$ は時刻 $t$ に依存しない量だ。 だから、 $v(t)^2 + 2gh(t)$ という量に対して、名前を付けたかったら付けてもいい」

僕「《不変なものには名前を付ける価値がある》」

ミルカ「そういうこと」

テトラ「なるほどです。でも、《それ》に名前が付いていないということは……？」

ミルカ「うれしさの度合いが違うんだろうな」

テトラ「うれしさの度合い……し、しつこくてすみません。 あたしは、 $v(t)^2$ ではなくて $\frac12mv(t)^2$ の方に名前を付ける気持ちがまだわかっていないようです。 これは質量が $m$ で時刻 $t$ の速度が $v(t)$ である質点の《運動エネルギー》ですよね」

僕「そうだね……それを考えるのがうれしい理由って何だろう」

テトラ「どうして $m$ を掛けなくちゃいけないんでしょうか」

僕「うーん、たとえば、 $v(t)^2 + 2gh(t)$ だと質量 $m$ のことは考えていないよね。 式に $m$ が組み込まれていないから」

テトラ「それはわかりますが……質量 $m$ が入っているとうれしいんでしょうか。 どうしてそんなに文字を増やして複雑な式にするんだろう……ってつい思ってしまいます。 自然に導けるなら納得できるんですが」

ミルカ「それでは《運動エネルギー》の方ではなく《位置エネルギー》の方から考えてみよう」

テトラ「《位置エネルギー》の方から？」

ミルカ「それがテトラの求めるような自然な導出かどうかはわからないけれど」

テトラ「はい」

ミルカ「《位置エネルギー》を考えるため、質点を高さ $s$ から自由落下させるようすを考えることにする」

質点の自由落下

ミルカ「こんな設定だ」

• 地上からの高さを $x$ 軸で表すことにする（上を正の向きとする）。地表を原点とする。
• 質点の質量を $m$ とする。
• 時刻を $t$ で表す。
• 自由落下させる瞬間の時刻を $t = 0$ とする。
• 時刻 $t$ における質点の位置を $h(t)$ で表す。
• 時刻 $t$ における質点の速度を $v(t)$ で表す。
• 質点の初めの位置を $h(0) = s$ とする。
• 質点の初速度を $v(0) = 0$ とする。
• 重力加速度の大きさを $g$ とする。

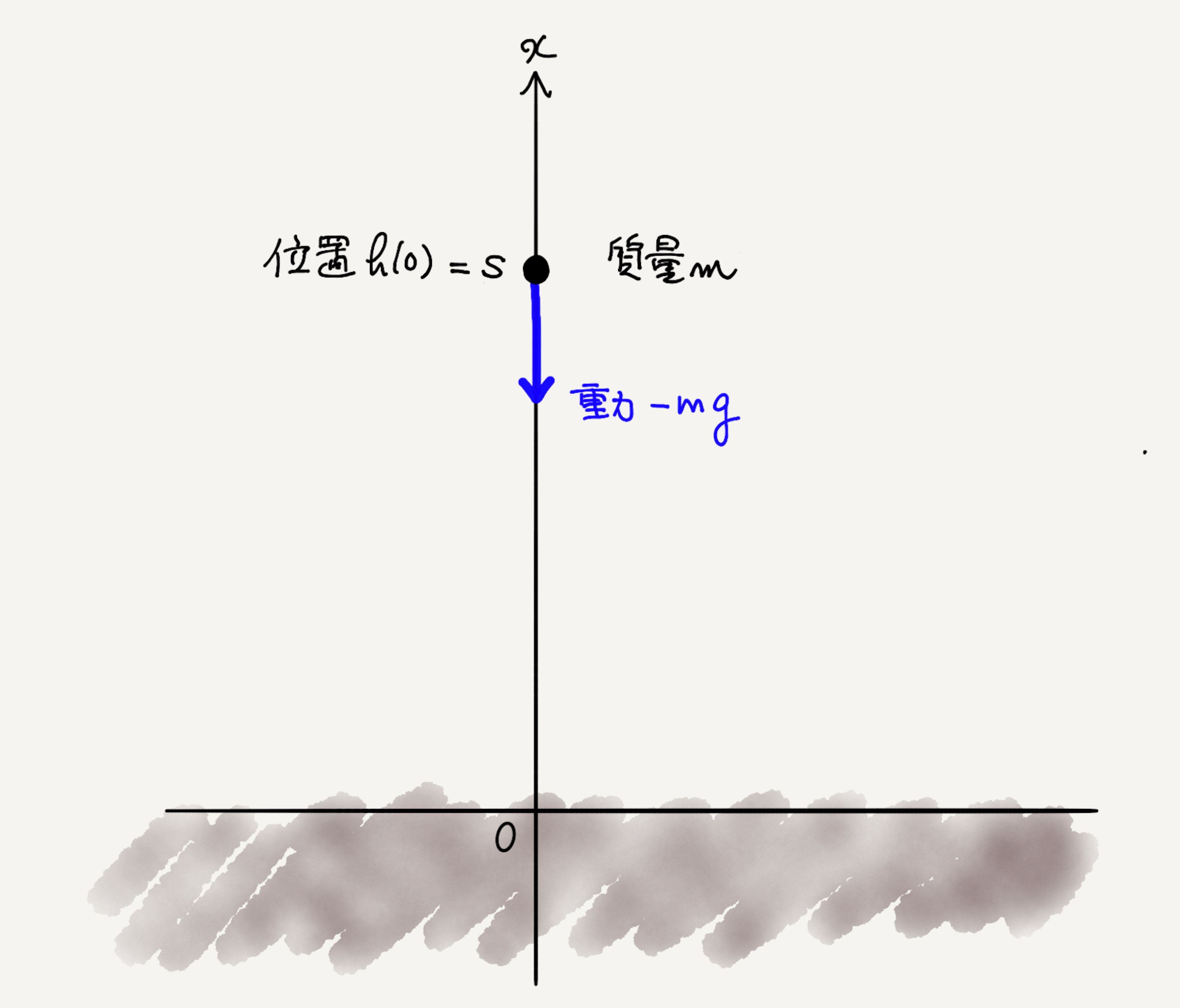
テトラ「はい、わかります。質点の初めの位置が $h(0) = s$ で、初速度が $v(0) = 0$ ですね」

僕「初速度が $v(0) = 0$ ということは、そっと質点を落とすわけだね」

ミルカ「《力学的エネルギー保存の法則》を使えば、地上に達したときの速度 $V$ はすぐに求められる。テトラ？」

テトラ「え、えっと。《力学的エネルギー》は《運動エネルギー》と《位置エネルギー》の和でした。 それで、それで……あっ、はい。大丈夫です。 手を離した瞬間の《力学的エネルギー》は…… $$ \underbrace{\tfrac12m0^2}_{\REMTEXT{運動エネルギー}} + \underbrace{mgs}_{\REMTEXT{位置エネルギー}} $$ ……です。速度が $0$ なので《運動エネルギー》は $0$ になります」

僕「そうだね」

テトラ「それから、地上に達した瞬間の《力学的エネルギー》は…… $$ \underbrace{\tfrac12mV^2}_{\REMTEXT{運動エネルギー}} + \underbrace{mg0}_{\REMTEXT{位置エネルギー}} $$ ……です。今度は高さが $0$ なので《位置エネルギー》が $0$ になります」

ミルカ「そう」

テトラ「《力学的エネルギー保存の法則》から、この二つの時点での《力学的エネルギー》が等しくなります。 それで…… $$ \begin{align*} \tfrac12m0^2 + mgs &= \tfrac12mV^2 + mg0 && \REMTEXT{《力学的エネルギー保存の法則》から} \\ mgs &= \tfrac12mV^2 && \REMTEXT{（$\heartsuit$）} \\ 2gs &= V^2 && \REMTEXT{両辺に$2/m$を掛けた} \\ V^2 &= 2gs && \REMTEXT{両辺を入れ換えた} \\ V &= -\SQRT{2gs} && \REMTEXT{$V < 0$だから} \\ \end{align*} $$ ……ですか？」

ミルカ「それでいい。 これで地面に達するときの速度 $V = -\SQRT{2gs}$ は得られる」

テトラ「あの……」

ミルカ「テトラが途中で書いたこの式（$\heartsuit$）に注目しよう。この式は何を表しているか」

テトラ「《力学的エネルギー保存の法則》です。あの、ミルカさん。 あたしが知りたいのは、どうして $\frac12mV^2$ という式に注目するか、なんですが……」

僕「この式は《位置エネルギー》が《運動エネルギー》に等しいといってるよね」

ミルカ「そうだ。いま考えた質点の自由落下では、 そっと手を離した瞬間の《位置エネルギー》が、地上に達した瞬間にはすべて《運動エネルギー》に変わったといえる」

僕「うん」

テトラ「……」

ミルカ「それは《力学的エネルギー保存の法則》を言い換えているだけだが、ここから、 テトラの疑問解消のために考えを進めていこう。 私たちはどうやって、質量 $m$ の質点を高さ $s$ に置いたのか」

テトラ「どうやって置いたか……ですか？」

ミルカ「そうだ。私たちはどうやって、質量 $m$ の質点を高さ $s$ に置いたのか。 それはとりも直さず、 私たちはどうやって、質量 $m$ の質点に $mgs$ という《位置エネルギー》を与えたかに答えることになる」

僕「なるほど、そういう展開になるんだ。

テトラ「？」

僕「僕たちは、質量が $m$ の質点に力を掛けて、高さ $s$ まで動かしたんだろうね」

ミルカ「そう考えてみる」

テトラ「質点に力を掛けて動かす……それはそうでしょうけれど……？」

ミルカ「地上から高さ $s$ まで《静かに持ち上げる》と考えてみよう」

僕「《静かに持ち上げる》というのは《速度を小さくして》ということだよね」

ミルカ「そう。とても小さくして」

テトラ「地上にある質点を $s$ まで持ち上げる……何を考えれば、考えたことになるんでしょう」

ミルカ「質量 $m$ の質点を持ち上げるためには力が必要になる」

テトラ「は、はい。そうですね。力がなければ持ち上がりませんから」

ミルカ「では、質量 $m$ の質点を持ち上げる力を $F$ としたとき、 $F$ を式で書けるだろうか」

テトラ「質量が $m$ で、重力加速度が $g$ ですから、必要な力は $F = mg$ でしょうか？」

ミルカ「$F = mg$ と $F = -mg$ でどちらが正しいか」