![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png)
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕：数学が好きな高校生。
テトラちゃん：僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
ミルカさん：数学が好きな高校生。 僕のクラスメート。長い黒髪の《饒舌才媛》。
ここは図書室。
ミルカさんとテトラちゃんと僕。三人で連分数について数学トークを続けている。
僕たちは、さまざまな話題がつながっていくのを楽しんできた（第267回参照）。
でもミルカさんはさらに進もうとしている。
ミルカ「では、先に進もう。 いまは $f$ と $g$ という二つの関数を合成することで、私の《カード》を表すことを試みた。 連分数を関数の目で見たといえる」
ミルカさんの《カード》
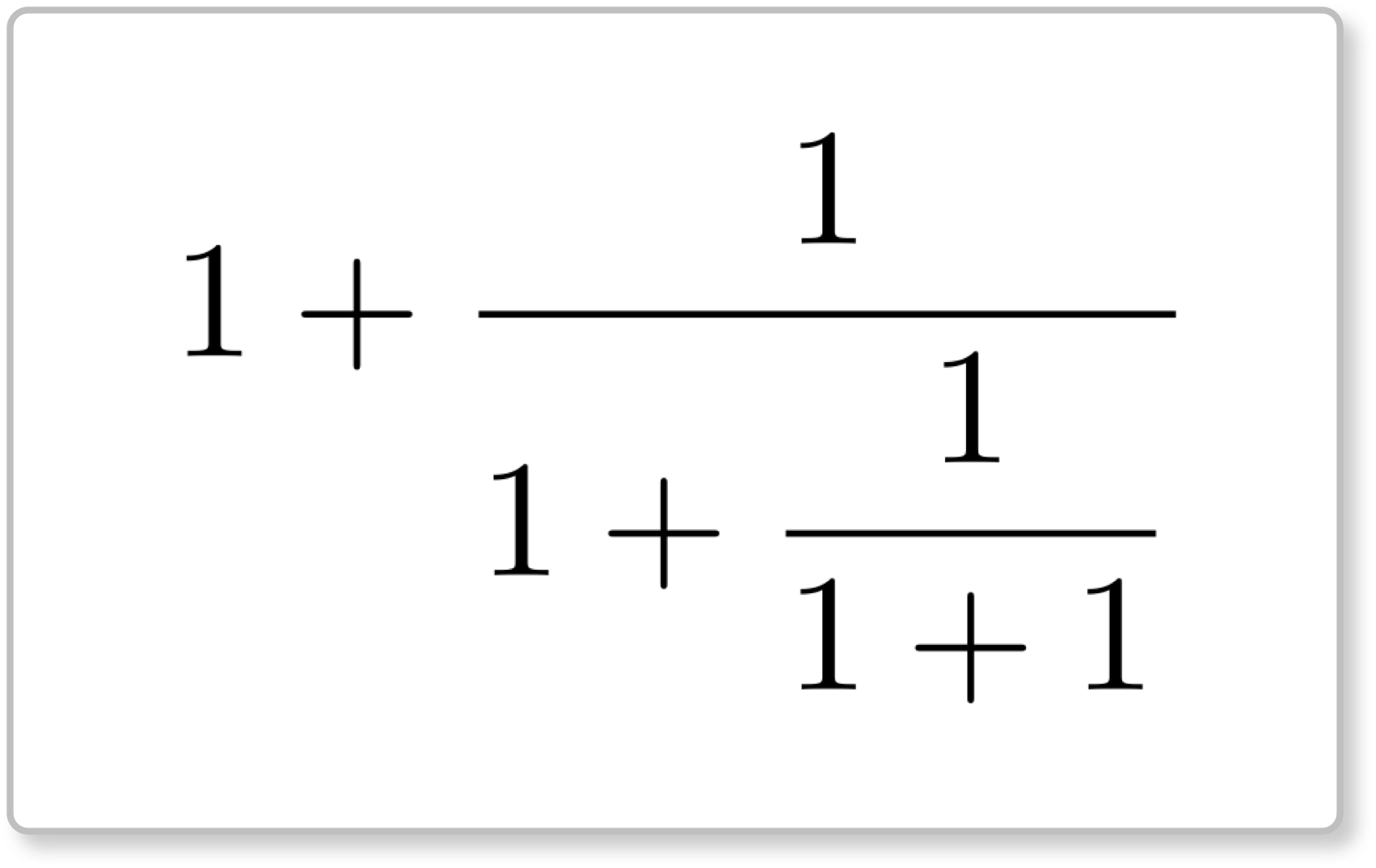
僕「そうだね。僕たちが用意したのは二つの関数 $f$ と $g$ で、 それを組み合わせて、ミルカさんの《カード》の連分数を構成できた」
二つの関数 $f$ と $g$
$$ \begin{align*} f(x) &= 1 + x \\ g(x) &= \frac1x \end{align*} $$
ミルカさんの《カード》を構成する $$ \begin{align*} \phi_2(\FBOX{1}) &= \FUN f{\FUN g{\FUN f{\FUN g{\FUN f{\FBOX{1}}}}}} \\ &= 1 + {\dfrac{1}{1 + {\dfrac{1}{1+\FBOX{1}}}}} \\ \end{align*} $$
テトラ「ここから先のお話が、まだあるんでしょうか」
ミルカ「いくらでも先がある。たとえば、 $f$ と $g$ というのは別の関数として扱ってきたが、 これをより一般化した枠組みに入れ込んでみることにしよう」
テトラ「一般化した枠組み……？」
僕「いやいや、 $f(x) = x + 1$ と $g(x) = 1/x$ とはまったく別の関数だよね」
テトラ「一般化……ということは、何か文字を導入するということですか。 《文字の導入による一般化》という方法を使って」
僕「うーん、でもそれは、たとえば $x + 1$ を $ax + b$ と見なすようなときには使えるけど、 和と逆数は式の形からまったく違うのに……表記がまったく違うのに、どうするんだろう」
ミルカさんは、僕とテトラちゃんを交互に見てから、唇に人差し指を当てる。
ミルカ「私たちは表記と値について考えてきた。 表記を一般化することによって、新しい視座が得られないかどうか見てみよう」
テトラ「表記を一般化……」
ミルカ「$x + 1$ と、 $1/x$ とはまったく違うようだけれど、 分数という表記を使えば、両者はそっくりに見える」
$$ \frac{x + 1}{1}\qquad\REMTEXT{と}\qquad \frac{1}{x} $$
テトラ「なるほど……？」
僕「両方とも分数という意味では似てるけど、そっくり……？」
ミルカ「こう表記すればどうか」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 440本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方／すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加（2019年8月2日）
![[icon]](https://img.hyuki.net/20220619121014-abd58cfc2ab436f4.png)