![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
ミルカさん:数学が好きな高校生。 僕のクラスメート。長い黒髪の《饒舌才媛》。
ある日の放課後。
僕が図書室に行くと、テトラちゃんが熱心に書き物をしていた。
僕「テトラちゃん、何を書いてるの?」
テトラ「あっ、先輩! グラフですっ!」
僕「グラフ……何のグラフ?」
テトラ「連分数のグラフです。あ、いいえ、違いますね。 連分数のグラフといいますか……数列のグラフです」
僕「?」
テトラ「あのですね。 あたしがもらった《カード》とミルカさんの《カード》から、 調和数のことや、 連分数のことを考えたじゃないですか」
僕「そうだね。いろんな話題が繋がって楽しかった」
テトラちゃんの《カード》
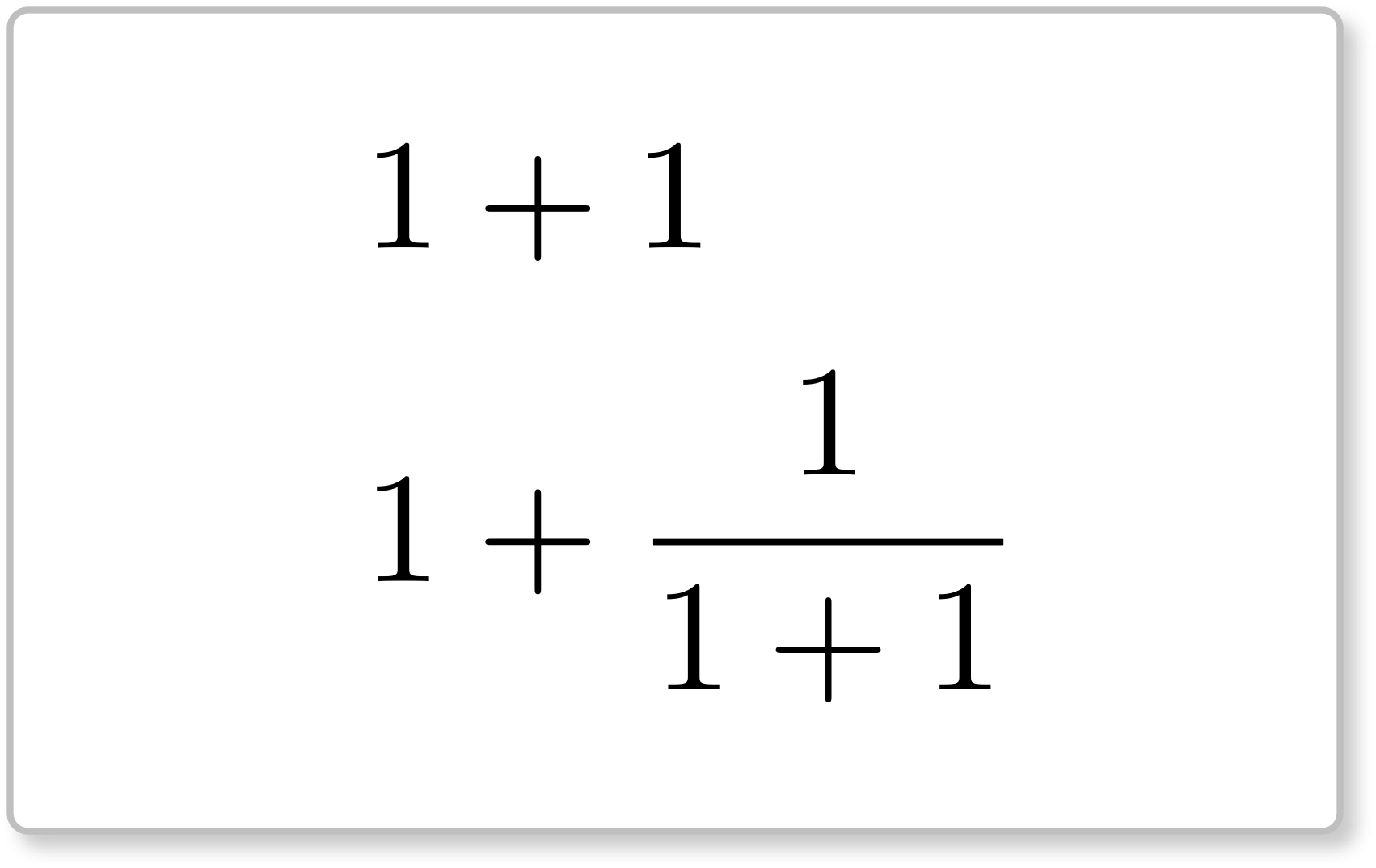
ミルカさんの《カード》
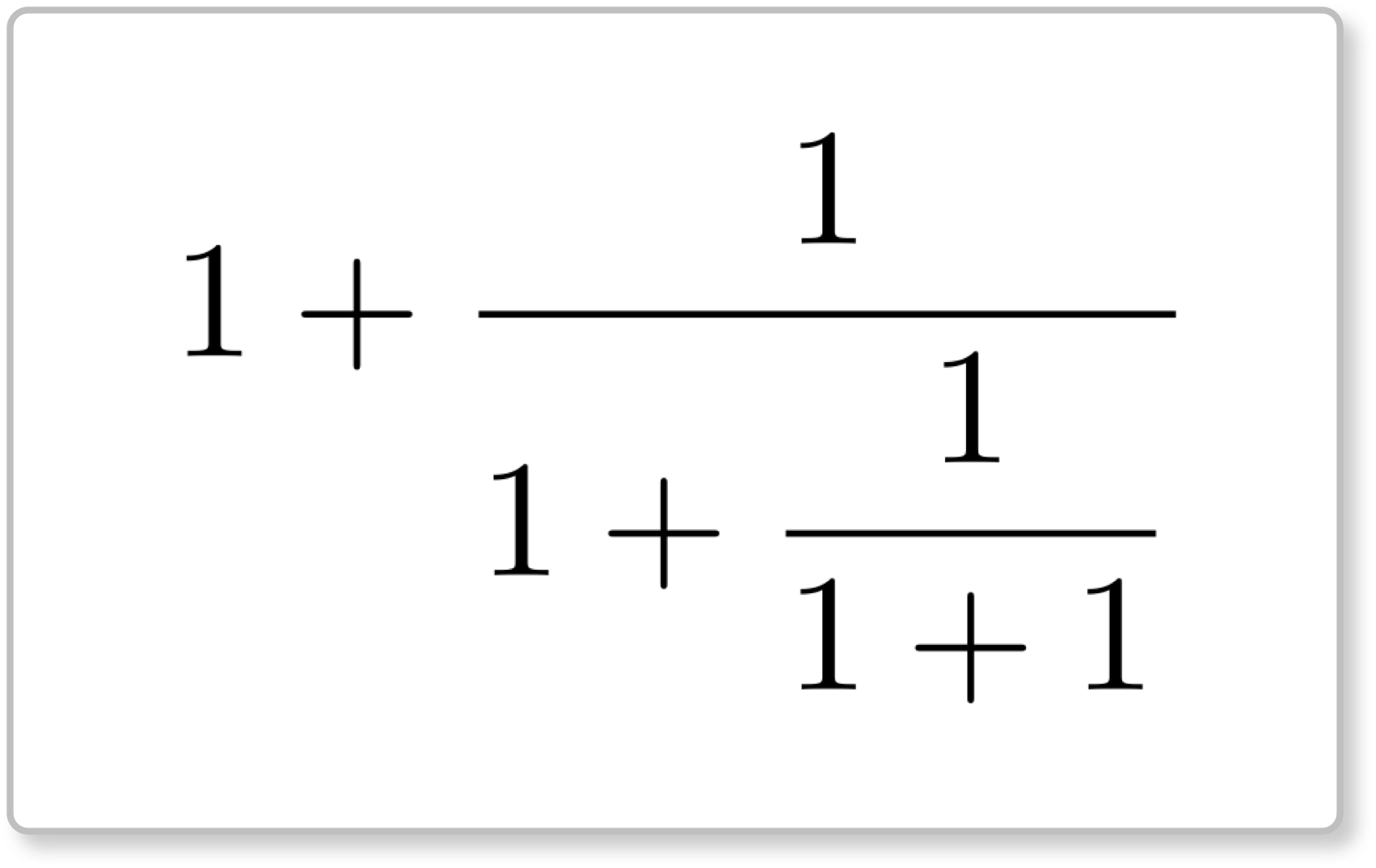
テトラ「はい。不等式で大きさを調べたり、極限を考えたりしました。 でも、あたし、グラフを描いていなかったことに気付いたんです」
僕「なるほどね。一般項が $H_n$ で表される数列 $H_1,H_2,H_3,\ldots$ のグラフを描くとか?」
$$ H_n = \frac11 + \frac12+ \cdots + \frac1n $$テトラ「はいはい、そうです。それから、連分数で表せる $\phi_n$ もです。 $$ \phi_n = 1 + \dfrac{1}{ 1 + \dfrac{1}{ 1 + \dfrac{1}{\ddots\dfrac{1}{ 1 + \dfrac11 }}}} \quad\REMTEXT{(横線$n$本)} $$ これを使った、 $$ \phi_1,\phi_2,\phi_3,\ldots $$ のグラフも描きます。グラフだと値の変化がわかりやすくなりますから」
僕「確かに」
テトラ「$y = H_n$ のグラフはこうです」
$y = H_n$ のグラフ
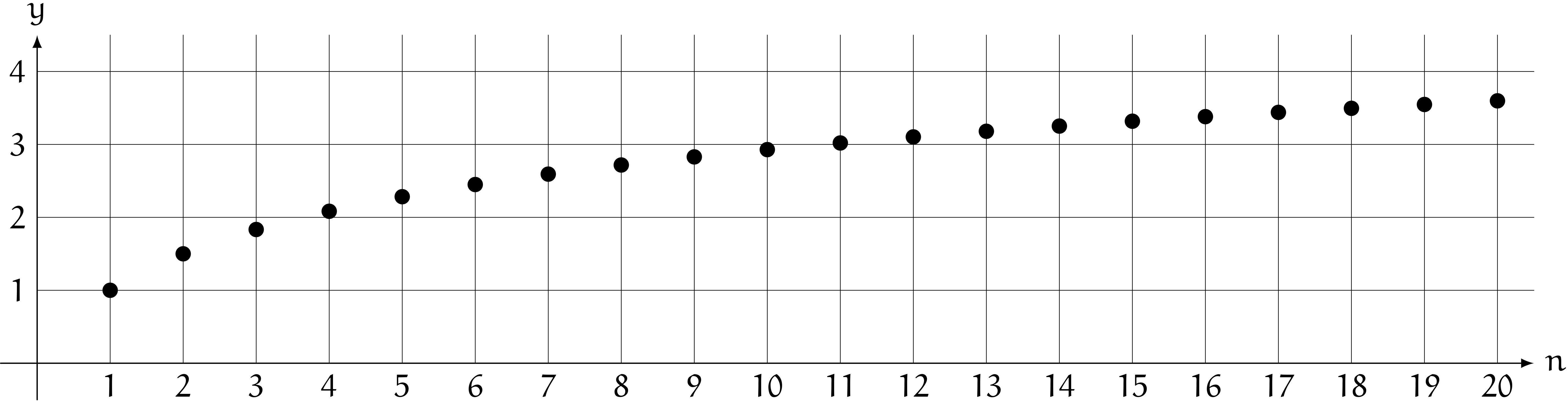
僕「なるほどね。 $H_n$ の方は、 $n \to \infty$ で $H_n \to \infty$ になることを証明したから、正の無限大に発散するはず」
テトラ「はい、そうですね。グラフではじわじわ増えていく感じなんですね」
僕「$\phi_n$ も描いたの?」
テトラ「はい。 $y = \phi_n$ のグラフはこうなります。わかりにくかったので、 $y$ 方向に引き延ばしてあります」
$y = \phi_n$ のグラフ
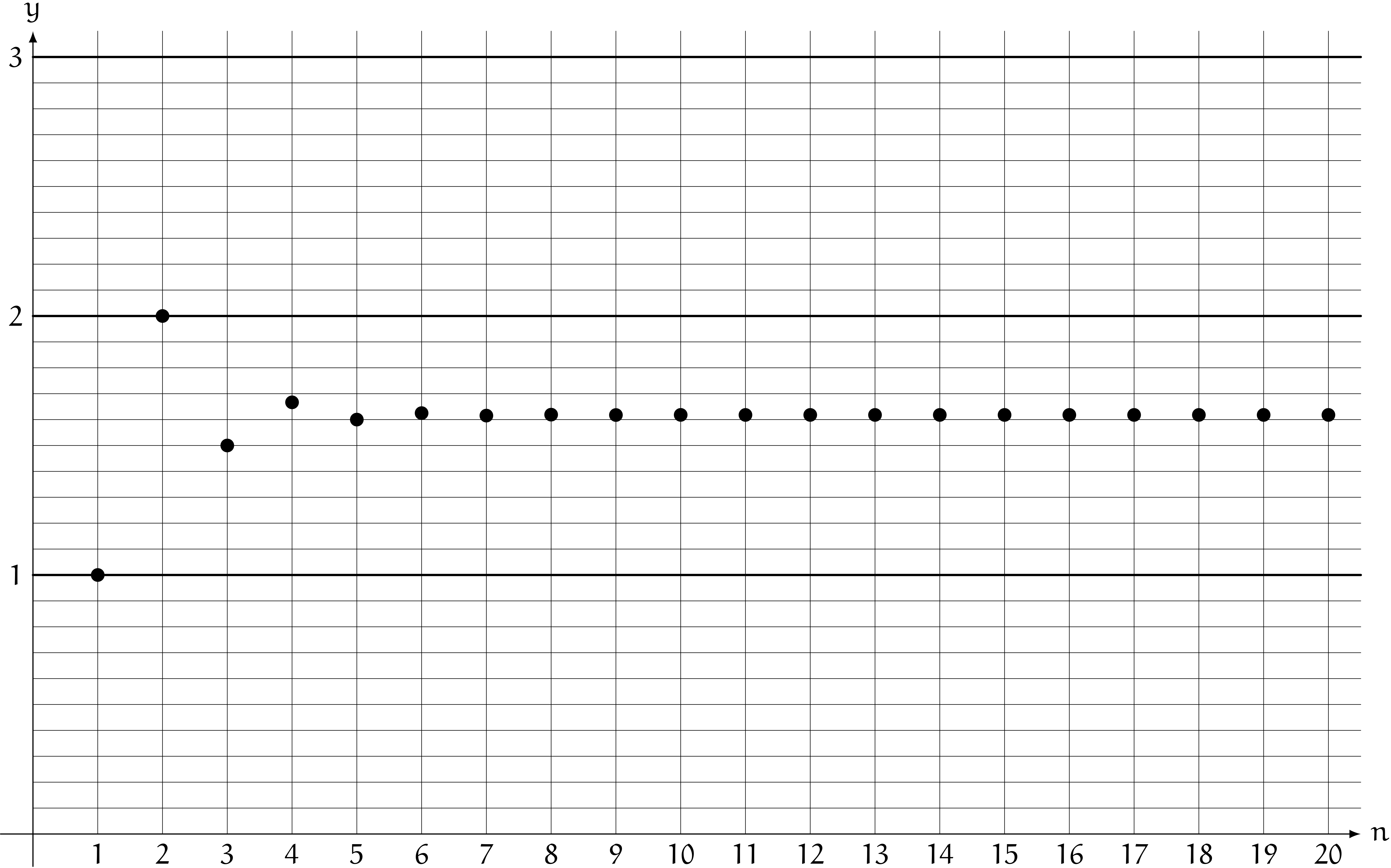
僕「へえ……こんな感じになるんだ。すぐに収束しちゃうんだなあ……」
テトラ「はい。 $\phi_n$ の方は、 $n \to \infty$ で $\phi_n \to \phi$ に収束します。黄金比 $\phi$ が極限値です」
僕「$\phi_n = \frac{F_{n+1}}{F_n}$ だったよね」
テトラ「そうです。 $\phi_n$ は、フィボナッチ数列の隣り合う項の比でした(第264回参照)……それを計算してみると、 $\phi_n$ の値は増加と減少が交互にやってくるようです」
僕「ああ、そうなんだ」
テトラ「え?」
僕「うん、あのね、 $F_n < F_{n+1}$ だから、つい $\phi_n$ も単調増加すると思っちゃったんだよ。錯覚、錯覚。勘違い、勘違い。 フィボナッチ数列 $F_n$ が増加するからといって、その比 $\phi_n$ まで増加するとは限らないよね。当たり前の話」
テトラ「ああ……そういうことですか。 具体的に計算するとよくわかります。こんなふうになりましたから」
$\phi_n$ の表
$$ \begin{array}{llll} \phi_{ 1} &= 1/1 &= 1 \\ \phi_{ 2} &= 2/1 &= 2 \\ \phi_{ 3} &= 3/2 &= 1.5 \\ \phi_{ 4} &= 5/3 &= 1.\dot6 \\ \phi_{ 5} &= 8/5 &= 1.6 \\ \phi_{ 6} &= 13/8 &= 1.625 \\ \phi_{ 7} &= 21/13 &= 1.6\dot1538\dot4 \\ \phi_{ 8} &= 34/21 &= 1.6\dot19047\dot6 \\ \phi_{ 9} &= 55/34 &= 1.6\dot176470588235294\dot1 \\ \phi_{10} &= 89/55 &= 1.6\dot1\dot8 \\ \phi_{11} &= 144/89 &= 1.6\dot1797752808988764044943820224719101123595505\dot6 \\ \phi_{12} &= 233/144 &= 1.6180\dot5 \\ \phi_{13} &= 377/233 &= 1.\dot618025751072961373390557939914163090128755364806866952789699570815450643776824034334763948497854077253218884120171673819742489270386266094420600858369098712446351931330472103004291845493562231759656652360515021459227467811158798283\dot2 \\ \phi_{14} &= 610/377 &= 1.\dot61803713527851458885941644562334217506631299734748010610079575596816976127320954907\dot1 \\ \phi_{15} &= 987/610 &= 1.\dot618032786885245901639344262295081967213114754098360655737704\dot9 \\ \phi_{16} &= 1597/987 &= 1.\dot61803444782168186423505572441742654508611955420466058763931104356636271529888551165146909827760891590678824721377912867274569402228976697\dot0 \\ \phi_{17} &= 2584/1597 &= 1.\dot618033813400125234815278647463994990607388854101440200375704445835942391984971822166562304320601127113337507827175954915466499686912\dot9 \\ \phi_{18} &= 4181/2584 &= 1.618\dot03405572755417956656346749226006191950464396284829721362229102167182662538699690402476780185758513931888544891640866873065015479876160990712074\dot3 \\ \phi_{19} &= 6765/4181 &= 1.\dot61803396316670652953838794546759148529060033484812245874192776847644104281272422865343219325520210475962688352068883042334369767998086582157378617555608706051183927290121980387467113130829944989237024635254723750298971537909591006936139679502511360918440564458263573307821095431714900741449414015785697201626405166228175077732599856493\dot6 \\ \phi_{20} &= 10946/6765 &= 1.6\dot180339985\dot2 \\ \end{array} $$
僕「これは……」
テトラ「$\phi_1 = 1$ から $\phi_2 = 2$ では大きくなり、 $\phi_2 = 2$ から $\phi_3 = 1.5$ では小さくなり、 $\phi_3 = 1.5$ から $\phi_4 = 1.\dot6$ では大きくなり……と、 大きくなるのと小さくなるのが交互にやってきます。 $\phi_7$ より後はぜんぶ $1.61\cdots$ になりますから、グラフではもう区別つかないですね」
僕「$\phi_{ 4} = 1.\dot6$ というのは $\phi_4 = 1.666\cdots$ のことだよね。 $\phi_4 = 1.\dot6 = 1.666\cdots$ から $\phi_{ 5} = 1.6$ は小さくなってる」
テトラ「はい、そうです。 小数表記で繰り返しになる範囲は、数字の上にドットを打ちました。 たとえば、 $$ \phi_{ 7} = 21/13 = 1.6\dot1538\dot4 $$ というのは、 $1$ から $4$ までを繰り返す、 $$ \phi_{ 7} = 21/13 = 1.6\FBOX{15384}\,\FBOX{15384}\,\FBOX{15384}\,\FBOX{15384}\,\cdots $$ のことです」
僕「おもしろいなあ。 $\phi_n = \frac{F_{n+1}}{F_n}$ だから必ず有理数になる。 だから、小数表記すると必ずどこかで割り切れるか循環するんだけど、 ときどきものすごく桁数が多くなる小数もあるんだね」
テトラ「そうなんですよ。びっくりしました。特に $\phi_{19}$ がものすごいですっ!」
$$ \begin{array}{rcl} \phi_{19} &=& 6765/4181 \\ &=& 1.\dot6180339631667065295383879454675914852906\\ & & \phantom{1.}0033484812245874192776847644104281272422\\ & & \phantom{1.}8653432193255202104759626883520688830423\\ & & \phantom{1.}3436976799808658215737861755560870605118\\ & & \phantom{1.}3927290121980387467113130829944989237024\\ & & \phantom{1.}6352547237502989715379095910069361396795\\ & & \phantom{1.}0251136091844056445826357330782109543171\\ & & \phantom{1.}4900741449414015785697201626405166228175\\ & & \phantom{1.}077732599856493\dot6 \\ \end{array} $$僕「これを根気よく計算するなんて、さすが!」
テトラ「あ、あの……」
僕「うん、やっぱりテトラちゃんだね!!」
テトラ「あの……おほめいただいてすみませんが、あたし、WolframAlphaを使ってしまいました……」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2019年8月9日)