![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
ミルカさん:数学が好きな高校生。 僕のクラスメート。長い黒髪の《饒舌才媛》。
テトラ「ミルカさんが先ほどおっしゃっていたことを思い出していました」
ミルカ「?」
テトラ「《分母と分子の交換》は《表記》に対する操作……というお話です」
ミルカ「《逆数を得る》は《値》に対する操作」
テトラ「それです! 《表記》と《値》の違いについて、 話題に出るたびに『なるほど!』と思いますが、『まだまだわかっていないぞ』とも思います」
ミルカ「ふむ」
テトラ「たとえば、分数で《分母と分子の交換》をすると《逆数を得る》というのは『なるほど、言われてみれば確かに』と思います。 その……何というんでしょうか、表記と値の結びつきを意識していなかったなあ……と思うんです」
ミルカ「そもそも、分数という用語自体がそうだな」
テトラ「ああ……」
ミルカ「分数というとき、 私たちは分母に $0$ 以外の数を書き、分子に数を書いた形を思い浮かべる。 分母と分子の二つの数のペアを使って数を表したものを分数と呼んでいる。 つまり分数という用語はそもそも《表記》を意識しているといえる」
僕「なるほど」
テトラ「ええと、逆数の方は《値》を意識している……?」
ミルカ「ある数 $x$ の逆数というのは、 $x$ に掛けると $1$ に等しくなる数だから、そもそも《値》を意識している」
テトラ「分母と分子を交換したものも……逆数ですよね?」
ミルカ「分数で表した $0$ 以外の数があったとする。たとえば $\frac23$ のように。 その分母と分子を交換して得られた分数、たとえば $\frac32$ の値は、 もちろん元の分数 $\frac23$ が表している値の逆数を表している。 $\frac23$ と $\frac32$ の積は $1$ に等しいからだ。 しかし、分母と分子を交換した数というのが逆数の定義なのではない。 逆数は分数で表されたものだけに使う用語ではないからだ」
テトラ「なるほどです」
僕「《分数》は《表記》を意識している用語という言い方をするなら、 《小数》も《表記》を意識している用語になるね」
テトラ「《○○数》という言い回しでも、何を意識しているかは違うんですね。 えっと、では《整数》はどちらになるんでしょう……《値》でしょうか」
ミルカ「《整数》は《値》を意識した用語だな。 たとえば、『$\frac{200}{100}$ は整数』だし、『$2.0$ は整数』といえる。 分数で表記しようとも、小数点を付けようとも、整数は整数だ」
僕「$1.999\cdots$ は整数だね」
テトラ「……もしかしたら、あたし、小学校のときに悩んだことがいま解決したかもしれません!」
僕「何を悩んでいたの? 算数ってこと?」
テトラ「たぶん、分数の習いたてのときです。 $$ \frac14 $$ が出てきました。 $4$ 分の $1$ です。大きな丸いピザが出てきて、 $4$ つに切ってそのうちの $1$ つが $4$ 分の $1$ です、みたいなお話を先生がしました」
※「いらすとや」さんのイラストをもとにしています。
ミルカ「……」
僕「……それで?」
テトラ「『$4$ つに切ってそのうちの $1$ つが $4$ 分の $1$』と言われて、あたしは『なるほど』と思いました。 黒板には、 $$ \frac14 $$ と書いてありました。ですから、あたしは……
僕「……それは、正しいよね?」
テトラ「えとえと、正しいんですけど、あたしはそこからしばらくジャンプできなかったんです」
僕「ジャンプ?」
テトラ「ピザの話題が終わった後で、授業が進んで、 $\frac14$ が $0.25$ に等しいという話になったとき、 あたしは大混乱してしまいました」
ミルカ「……」
僕「うーん……ごめんね、よくわからないんだけど」
テトラ「あのですね。小学生のあたしは、 $\frac14$ を『$4$ つに切ってそのうちの $1$ つ』を表していると思ったんです。 つまり、文字通りこんな操作を表しているって……」
テトラちゃんは両手をバタバタさせて、ピザを切って、選んで、食べるジェスチャをする。
食べるんだ。
僕「ははあ……それで?」
テトラ「はい、ピザを $4$ つに切ってそのうちの $1$ つ選ぶというのはとてもわかりやすい話でした。 でも、それがいきなり $0.25$ になったことに違和感を覚えたんです……あたし、説明下手ですね」
ミルカ「ジャンプできなかったというのは、 《表記》から《値》を得ることができなかったという意味かな」
テトラ「はい、そういう意味です。 $$ \frac14 $$ という分数は、 $4$ つに切って $1$ つ選ぶという操作を表しているというだけでは説明不十分なんです。 $\frac14$ という分数の《表記》は、 《ピザ全体が $1$ という値を表しているとき、 $4$ つに切ったうちの $1$ つが表している値》を表しているんです! ……って、 あたし、とても当たり前のことを話してますね」
僕「いや、でも、納得感というのはそういうものじゃないかなあ。 改めて説明すると、当たり前に聞こえる」
テトラ「ともかく《表記》と《値》を意識して分けて考えて、 ちゃんと《表記》から《値》を得ることが大事なのかも……と思ったんです」
ミルカ「ふむ」
僕「考えてみると、一つの数を《小数》で表記したり、 《分数》で表記したり、 あるいはまた《連分数》で表記するというのはおもしろいことだよね。 それぞれに違う風景が見えてくるから」
僕はそう言いながら、位取り記数法のことを考えていた。 $10$ 進法で見える風景と、 $2$ 進法で見える風景は確かに違う。
ユーリ「はいっ、ここで宣伝タイムです。 $2$ 進法で見える風景はシリーズ第11作、 『数学ガールの秘密ノート/ビットとバイナリー』 でお読みくださーい! $2$ 進法でどんな風景が見えるのか、あなたも体感せよ!」
僕「なんだいまの」
ミルカ「では、さらに別の風景を見ようか」
僕「え?」
テトラ「さらに別の風景……?」
ミルカ「私たちは連分数を使って数を表してきた。では、そこから関数を使って数を表すことを試みる」
僕「関数?」
ミルカ「スタートは私がもらった《カード》にしよう」
ミルカさんの《カード》
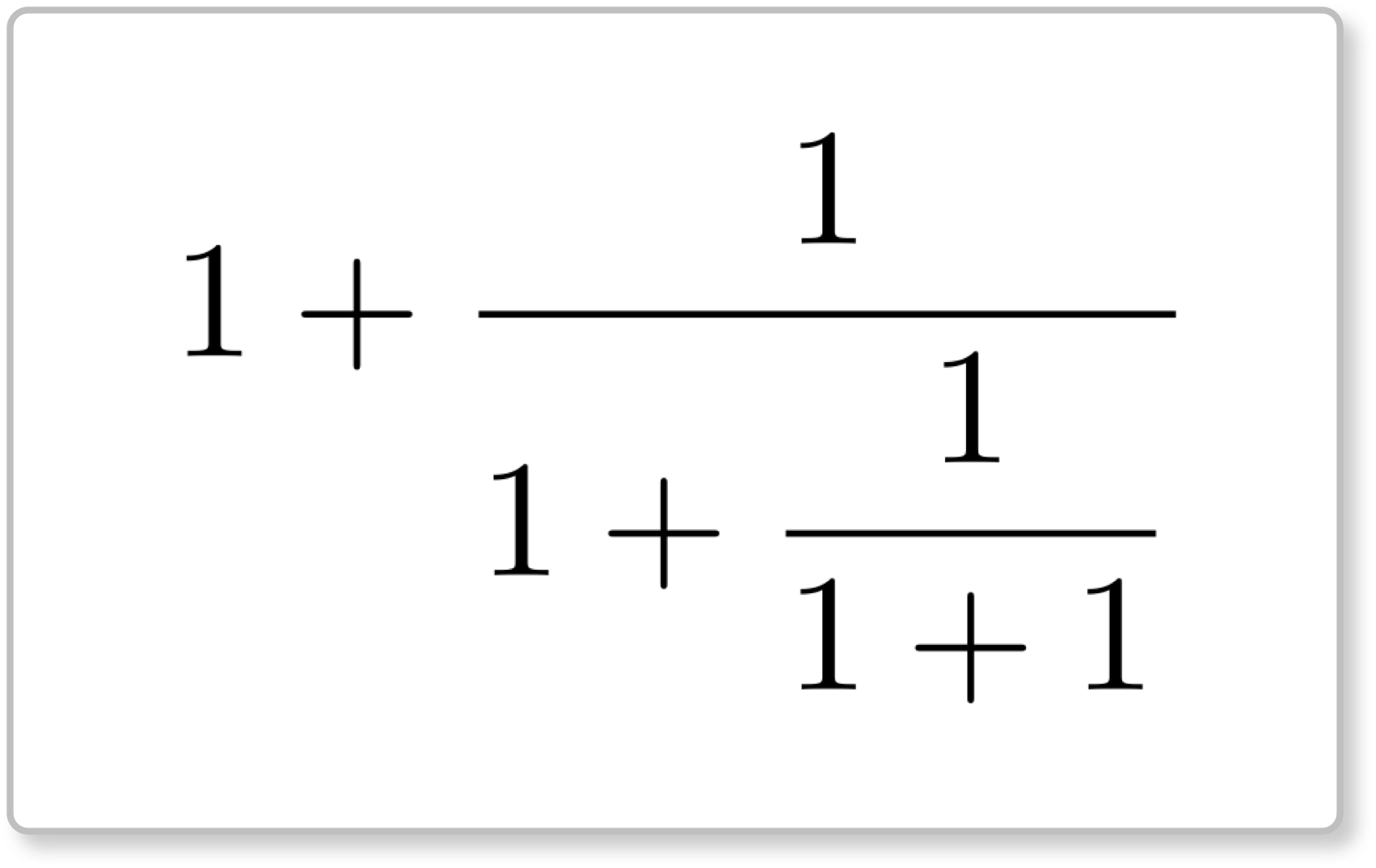
僕「うん、いいよ」
テトラ「はい……」
ミルカ「この連分数表記で表されている値を計算しようとするとき、私たちはどうするか」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2019年7月26日)